树模型是如何计算特征重要性的

最新推荐文章于 2025-11-02 13:06:46 发布

转载最新推荐文章于 2025-11-02 13:06:46 发布 · 7.9k 阅读

ML 同时被 2 个专栏收录

76 篇文章

订阅专栏

67 篇文章

订阅专栏

AI助手已提取文章相关产品：

前言

在特征的选择过程中，如果学习器（基学习器）是树模型的话，可以根据特征的重要性来筛选有效的特征。本文是对Random Forest、GBDT、XGBoost如何用在特征选择上做一个简单的介绍。

各种模型的特征重要性计算

Random Forests

袋外数据错误率评估
RF的数据是boostrap的有放回采样，形成了袋外数据。因此可以采用袋外数据（OOB）错误率进行特征重要性的评估。
袋外数据错误率定义为：袋外数据自变量值发生轻微扰动后的分类正确率与扰动前分类正确率的平均减少量。
（1）对于每棵决策树，利用袋外数据进行预测，将袋外数据的预测误差记录下来，其每棵树的误差为vote1,vote2,…,voteb
（2）随机变换每个预测变量，从而形成新的袋外数据，再利用袋外数据进行验证，其每个变量的误差是votel1,votel2,…votelb
Gini系数评价指标（和GBDT的方法相同）

GBDT

在sklearn中，GBDT和RF的特征重要性计算方法是相同的，都是基于单棵树计算每个特征的重要性，探究每个特征在每棵树上做了多少的贡献，再取个平均值。
在利用随机森林对特征重要性进行评估写的比较清楚了，但是还是有一点小的问题，比较ensemble模型零碎记录中对源代码的解析可以看出，前者计算中丢失了weighted_n_node_samples。

利用Gini计算特征的重要性
单棵树上特征的重要性定义为：特征在所有非叶节在分裂时加权不纯度的减少，减少的越多说明特征越重要。
沿用参考博客里的符号，我们将变量重要性评分（variable importance measures）用VIMVIM来表示，将Gini指数用GIGI来表示
节点m的Gini指数的计算公式为：
GIm=1−∑k=1|K|p2mkGIm=1−∑k=1|K|pmk2

其中，K表示有K个类别，pmkpmk表示节点m中类别k所占的比例。直观地说，就是随便从节点m中随机抽取两个样本，其类别标记不一致的概率。
特征XjXj在节点mm的重要性可以表示为加权不纯度的减少
VIMGinijm=Nm×GIm−Nl×GIl−Nr×GIrVIMjmGini=Nm×GIm−Nl×GIl−Nr×GIr

其中，GIlGIl和GIrGIr分别表示分枝后两个新节点的Gini指数。NmNm、NlNl、NrNr表示节点m、左孩子节点l和右孩子节点r的样本数。
如果，特征XjXj在决策树i中出现的节点在集合M中，那么XjXj在第i颗树的重要性为
VIMij=∑m∈MVIMjmVIMij=∑m∈MVIMjm

~~如果这样还不是很清晰的话，我们来举个例子（李航统计学习方法表5.1）

import numpy as np
from sklearn.tree import DecisionTreeClassifier
from sklearn.externals.six import StringIO
from sklearn import tree
import pydotplus

clf = DecisionTreeClassifier()
x = [[1,1,1,1,1,2,2,2,2,2,3,3,3,3,3],
     [1,1,2,2,1,1,1,2,1,1,1,1,2,2,1],
     [1,1,1,2,1,1,1,2,2,2,2,2,1,1,1],
     [1,2,2,1,1,1,2,2,3,3,3,2,2,3,1]
     ]
y =  [1,1,2,2,1,1,1,2,2,2,2,2,2,2,1]
x = np.array(x)
x = np.transpose(x)
clf.fit(x,y)
print clf.feature_importances_
feature_name = ['A1','A2','A3','A4']
target_name = ['1','2']
dot_data = StringIO()
tree.export_graphviz(clf,out_file = dot_data,feature_names=feature_name,
                     class_names=target_name,filled=True,rounded=True,
                     special_characters=True)
graph = pydotplus.graph_from_dot_data(dot_data.getvalue())
graph.write_pdf("WineTree.pdf")
print('Visible tree plot saved as pdf.')

可以得到树的划分过程图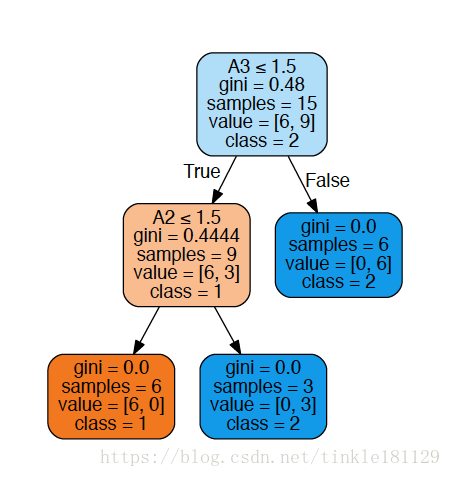
这里写图片描述
特征A3的重要性为 0.48×15−0.4444×9−0=3.20040.48×15−0.4444×9−0=3.2004
特征A2的重要性为 0.4444×9−0−0=3.99960.4444×9−0−0=3.9996
特征A1和A4的重要性都为0
所以该棵树上所有节点总的加权不纯度减少量为 3.2004+3.9996=7.33.2004+3.9996=7.3
对其进行归一化操作可以得到A1、A2、A3、A4的特征重要性为

[ 0. 0.55555556 0.44444444 0. ]

这是单棵树上特征的计算方法，推广到n棵树

VIMj=∑i=1nVIMijVIMj=∑i=1nVIMij

最后，把所有求得的重要性评分做一个归一化处理即可。

VIMj=VIMj∑i=1cVIMiVIMj=VIMj∑i=1cVIMi

其中cc为特征的总个数

XGBoost

关于XGBoost中特征重要性计算相关代码出现在xgboost/core.py L1203

    def get_score(self, fmap='', importance_type='weight'):
        """Get feature importance of each feature.
        Importance type can be defined as:
            'weight' - the number of times a feature is used to split the data across all trees.
            'gain' - the average gain of the feature when it is used in trees
            'cover' - the average coverage of the feature when it is used in trees
        Parameters
        ----------
        fmap: str (optional)
           The name of feature map file
        """

        if importance_type not in ['weight', 'gain', 'cover']:
            msg = "importance_type mismatch, got '{}', expected 'weight', 'gain', or 'cover'"
            raise ValueError(msg.format(importance_type))

        # if it's weight, then omap stores the number of missing values
        if importance_type == 'weight':
            # do a simpler tree dump to save time
            trees = self.get_dump(fmap, with_stats=False)

            fmap = {}
            for tree in trees:
                for line in tree.split('\n'):
                    # look for the opening square bracket
                    arr = line.split('[')
                    # if no opening bracket (leaf node), ignore this line
                    if len(arr) == 1:
                        continue

                    # extract feature name from string between []
                    fid = arr[1].split(']')[0].split('<')[0]

                    if fid not in fmap:
                        # if the feature hasn't been seen yet
                        fmap[fid] = 1
                    else:
                        fmap[fid] += 1

            return fmap

        else:
            trees = self.get_dump(fmap, with_stats=True)

            importance_type += '='
            fmap = {}
            gmap = {}
            for tree in trees:
                for line in tree.split('\n'):
                    # look for the opening square bracket
                    arr = line.split('[')
                    # if no opening bracket (leaf node), ignore this line
                    if len(arr) == 1:
                        continue

                    # look for the closing bracket, extract only info within that bracket
                    fid = arr[1].split(']')

                    # extract gain or cover from string after closing bracket
                    g = float(fid[1].split(importance_type)[1].split(',')[0])

                    # extract feature name from string before closing bracket
                    fid = fid[0].split('<')[0]

                    if fid not in fmap:
                        # if the feature hasn't been seen yet
                        fmap[fid] = 1
                        gmap[fid] = g
                    else:
                        fmap[fid] += 1
                        gmap[fid] += g

            # calculate average value (gain/cover) for each feature
            for fid in gmap:
                gmap[fid] = gmap[fid] / fmap[fid]
            return gmap

在XGBoost中提供了三种特征重要性的计算方法：

‘weight’ - the number of times a feature is used to split the data across all trees.
‘gain’ - the average gain of the feature when it is used in trees
‘cover’ - the average coverage of the feature when it is used in trees

简单来说
weight就是在所有树中特征用来分割的节点个数总和；
gain就是特征用于分割的平均增益
cover 的解释有点晦涩，在[R-package/man/xgb.plot.tree.Rd]有比较详尽的解释：(https://github.com/dmlc/xgboost/blob/f5659e17d5200bd7471a2e735177a81cb8d3012b/R-package/man/xgb.plot.tree.Rd)：the sum of second order gradient of training data classified to the leaf, if it is square loss, this simply corresponds to the number of instances in that branch. Deeper in the tree a node is, lower this metric will be。实际上coverage可以理解为被分到该节点的样本的二阶导数之和，而特征度量的标准就是平均的coverage值。

还是举李航书上那个例子，我们用不同颜色来表示不同的特征，绘制下图
这里写图片描述

import xgboost as xgb
import numpy as np
x = [[1,1,1,1,1,2,2,2,2,2,3,3,3,3,3],
     [1,1,2,2,1,1,1,2,1,1,1,1,2,2,1],
     [1,1,1,2,1,1,1,2,2,2,2,2,1,1,1],
     [1,2,2,1,1,1,2,2,3,3,3,2,2,3,1]
     ]
y =  [0,0,1,1,0,0,0,1,1,1,1,1,1,1,0]
x = np.array(x)
x = np.transpose(x)

params = {
    'max_depth': 10,
    'subsample': 1,
    'verbose_eval': True,
    'seed': 12,
    'objective':'binary:logistic'
}
xgtrain = xgb.DMatrix(x, label=y)
bst = xgb.train(params, xgtrain, num_boost_round=10)
fmap = 'weight'
importance = bst.get_score(fmap = '',importance_type=fmap)
print importance
print bst.get_dump(with_stats=False)
fmap = 'gain'
importance = bst.get_score(fmap = '',importance_type=fmap)
print importance
print bst.get_dump(with_stats=True)
fmap = 'cover'
importance = bst.get_score(fmap = '',importance_type=fmap)
print importance
print bst.get_dump(with_stats=True)

logs :

0:[f2<1.5] yes=1,no=2,missing=1,gain=3.81862,cover=3.75
    1:[f3<1.5] yes=3,no=4,missing=3,gain=1.4188,cover=2.25
        3:leaf=-0.3,cover=1
        4:leaf=0.0666667,cover=1.25
    2:leaf=0.36,cover=1.5

0:[f2<1.5] yes=1,no=2,missing=1,gain=2.69365,cover=3.67888
    1:leaf=-0.119531,cover=2.22645
    2:leaf=0.30163,cover=1.45243

0:[f1<1.5] yes=1,no=2,missing=1,gain=2.4414,cover=3.5535
    1:leaf=-0.107177,cover=2.35499
    2:leaf=0.302984,cover=1.19851

0:[f2<1.5] yes=1,no=2,missing=1,gain=1.92691,cover=3.49546
    1:leaf=-0.10337,cover=2.16893
    2:leaf=0.259344,cover=1.32653

0:[f1<1.5] yes=1,no=2,missing=1,gain=1.79698,cover=3.3467
    1:leaf=-0.095155,cover=2.24952
    2:leaf=0.263871,cover=1.09718

0:[f3<1.5] yes=1,no=2,missing=1,gain=1.56711,cover=3.26459
    1:leaf=-0.165662,cover=1.02953
    2:[f2<1.5] yes=3,no=4,missing=3,gain=0.084128,cover=2.23506
        3:leaf=0.0508745,cover=1.20352
        4:leaf=0.220771,cover=1.03154

0:[f1<1.5] yes=1,no=2,missing=1,gain=1.31036,cover=3.12913
    1:leaf=-0.0852405,cover=2.12169
    2:leaf=0.227708,cover=1.00744

0:[f2<1.5] yes=1,no=2,missing=1,gain=1.25432,cover=3.0361
    1:leaf=-0.0915171,cover=1.94381
    2:leaf=0.214414,cover=1.09229

0:[f0<2.5] yes=1,no=2,missing=1,gain=0.440551,cover=2.89962
    1:leaf=-0.0431823,cover=1.87075
    2:leaf=0.142726,cover=1.02887

0:leaf=0.0379022,cover=2.86568

使用weight的结果为