C++：栈与队列，优先级队列(+仿函数，反向迭代器，typename)

原创

已于 2022-10-09 09:54:40 修改 · 1k 阅读

4 ·

CC 4.0 BY-SA版权

文章标签：

#c++

于 2022-07-31 11:17:46 首次发布

本文详细介绍了栈、队列、优先级队列的原理、使用方法，包括适配器设计、栈与队列的典型题目解决方案，以及模仿实现的stack、queue和priority_queue。讨论了栈顶返回类型、仿函数和反向迭代器，以及deque与vector、list的区别。

3.优先级队列 priority_queue

易错点：

重点

（1）top()返回类型 const T& 的原因

（2）仿函数 #include

priority_queue代码

4.deque与vector，list对比

3.例子2：指向数组的原生指针，本身就是天然迭代器

六.反向迭代器

七.typename

一.栈与队列，优先级队列的介绍

2.适配器

适配器是一种设计模式 ( 设计模式是一套被反复使用的、多数人知晓的、经过分类编目的、代码设计经验的总结) ， 该种模式是将一个类的接口转换成客户希望的另外一个接口 。

二.栈与队列，优先级队列的使用

优先级队列的问题:优先级队列默认大的优先级高，传的是less仿函数，底层是一个大堆；
想控制小的优先级高，传greater仿函数，底层是一个小堆。这个反过来的，算是设计的一个失误。

（实际上less——大堆，greater——小堆，greater可理解为小堆下面越来越大）

#include<iostream>
#include<stack>
#include<queue>
#include <functional>
using namespace std;
namespace std
{
	void test_stack()            //栈
	{
		stack<int> s;
		s.push(1);
		s.push(2);
		s.push(3);
		s.push(4);

		while (!s.empty())
		{
			cout << s.top() << " ";
			s.pop();
		}
		cout << endl;
	}

	void test_queue()            //队列
	{
		queue<int> q;
		q.push(1);
		q.push(2);
		q.push(3);
		q.push(4);

		while (!q.empty())
		{
			cout << q.front() << " ";
			q.pop();
		}
		cout << endl;
	}

	void test_priority_queue()            //优先级队列
	{
		//priority_queue<int> pq;
		priority_queue<int, vector<int>, greater<int>> pq;

		pq.push(2);
		pq.push(5);
		pq.push(1);
		pq.push(6);
		pq.push(8);

		while (!pq.empty())
		{
			cout << pq.top() << " ";
			pq.pop();
		}
		cout << endl;
	}
}

int main()
{
	std::test_stack();
	std::test_queue();
	std::test_priority_queue();

	return 0;
}

三.栈和队列相关题目

1.155. 最小栈

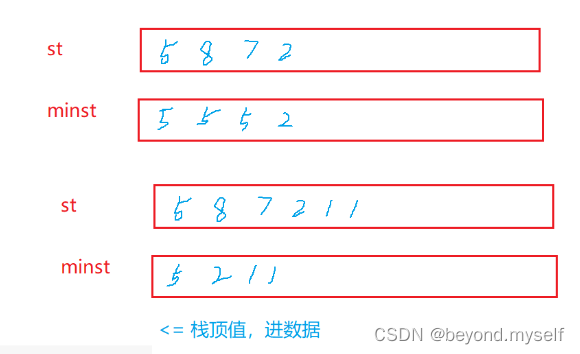
思路：用两个栈，st存放入的数据，minst存放入数据后的最小数据；

优化：minst存放入数据后的最小数据，如果后面再尾插的数据都没有这个数据大，minst就不尾插数据，如果尾插的数据 小于或等于 minst中最后一个数据，就尾插这个数据进minst。

举例：st第一个数据5，minst尾插一个5；st尾插8，8>5，minst不变；st尾插7，minst不尾插；st尾插2,2<5，尾插2；st尾插1,1<2，minst尾插1；st又尾插1,1=1，minst还要尾插1。（因为如果=时minst不尾插，pop数据时，st尾删一个1，minst就一个1，尾删后，st中还有一个1，最小值就乱了）

class MinStack {
public:
    MinStack() {
        //成员变量是自定义类型，默认生成够用
    }
    
    void push(int val) {
        _st.push(val);
        if(_minst.empty()||val<=_minst.top())
        {
            _minst.push(val);
        }
    }
    
    void pop() {
        if(_st.top()==_minst.top())
        {
            _minst.pop();
        }
        _st.pop();
    }
    
    int top() {
        return _st.top();
    }
    
    int getMin() {
        return _minst.top();
    }

private:
    stack<int> _st;    
    stack<int> _minst;    
};

2.栈的压入、弹出序列

栈的压入、弹出序列_牛客题霸_牛客网 (nowcoder.com)

class Solution {
public:
    bool IsPopOrder(vector<int> pushV,vector<int> popV) {
        stack<int> st;
        int popi=0;
        for(auto e: pushV)
        {
            st.push(e);
            while(!st.empty() && st.top()==popV[popi])
            {
                popi++;
                st.pop();
            }
        }
        return st.empty();
    }
};

3.150. 逆波兰表达式求值

过程：逆波兰表达式又称后缀表达式

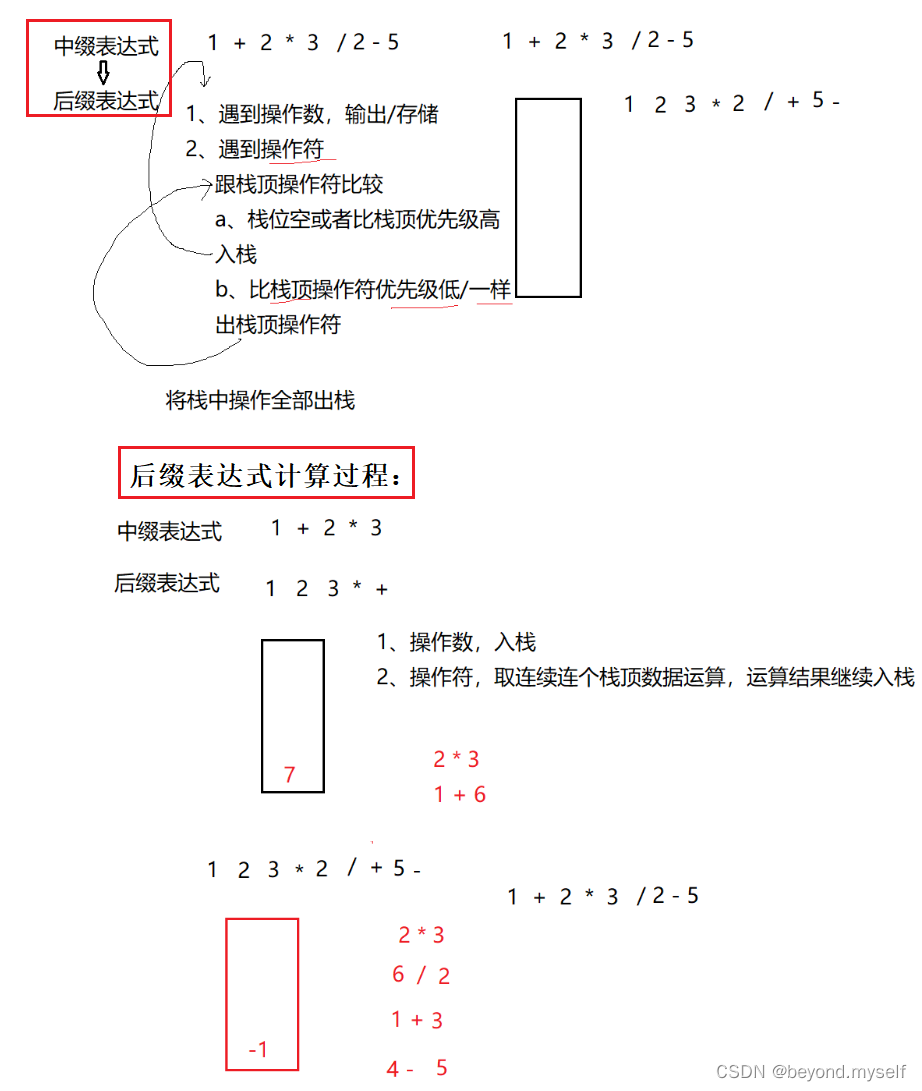
手敲：

class Solution {
public:
    int evalRPN(vector<string>& tokens) {
        stack<int> st;
        for(auto e:tokens)
        {
            if(e=="+"||e=="-"||e=="*"||e=="/")
            {
                int b=st.top();         //易错点1
                st.pop();

最低0.47元/天解锁文章