OpenGL中PBR着色器的实现

背景

刚来公司的第一个项目就是通过OpenGL加载汽车的3D模型，UI设计提供了基础色（Base_Color）、粗糙度（roughness）、金属度（metallic），就是按照PBR提供的材质。之前的加载鞋子模型采用的方案是Blinn-Phone光照模型，Blinn-Phone光照模型也可以实现汽车3D模型的效果，实现过程中需要调整漫反射、高光的参数达到一个比较满意效果，与真实的效果相比较很难令人信服。所以汽车3D模型采用PBR技术实现，下面就介绍下Android端PBR Shader的实现，由于PBR理论知识相对复杂，这里只介绍带贴图的PBR的实现对于文章中涉及的其他概念请自行查阅资料。

PBR基本原理和实现

满足以下条件的光照模型才能称之为PBR光照模型：

• 基于微平面模型（Be based on the microfacet surface model）。
• 能量守恒（Be energy conserving）。
• 使用基于物理的BRDF（Use a physically based BRDF）。

微平面模型

大多数PBR技术都是基于微平面理论。在此理论下，认为在微观上所有材质表面都是由很多朝向不一的微小平面组成，有的材质表面光滑一些，有的粗糙一些。
当光线射入这些微平面后，通常会产生镜面反射。对于越粗糙的表面，由于其朝向更无序，反射的光线更杂乱，反之，平滑的微平面，反射的光线更平齐。

从微观角度来说，没有任何表面是完全光滑的。由于这些微平面已经微小到无法逐像素地继续对其进行细分，因此我们只有假设一个粗糙度(Roughness)参数，然后用统计学的方法来概略的估算微平面的粗糙程度。
因此，粗糙度越高的表面，表面光线反射越分散，反之则越集中：

在实际的PBR实现中，粗糙度（Roughness）是用来调整PBR效果的一个重要参数之一
我们可以基于一个平面的粗糙度来计算出某个向量的方向与微平面平均取向方向一致的概率。这个向量便是位于光线向量𝑙和视线向量𝑣之间的中间向量，被称为半角向量(Halfway Vector)。

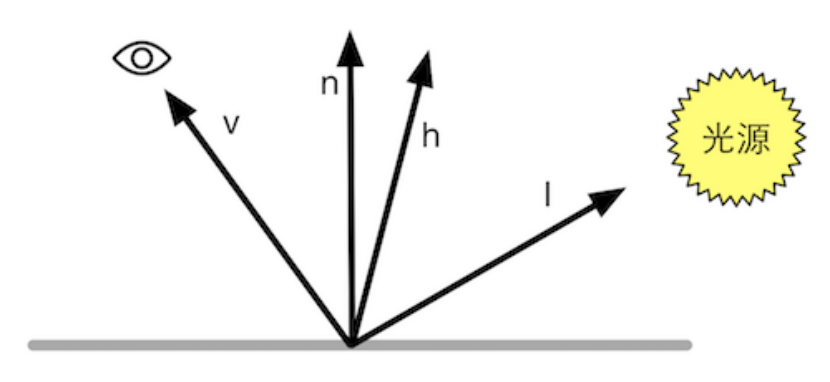
半角向量ℎ是视线𝑣和入射光𝑙的中间单位向量。
半角向量计算公式如下：

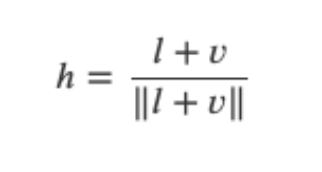
半角向量计算GLSL实现:

// lightPos是光源位置，viewPos是摄像机位置，FragPos是像素位置
vec3 lightDir   = normalize(lightPos - FragPos);
vec3 viewDir    = normalize(viewPos - FragPos);
vec3 halfwayDir = normalize(lightDir + viewDir);

能量守恒

在PBR中，能量守恒定律认为，出射的光线能量，永远不能超过入射光线的能量。在微平面模型中，对于一束光进入到进入到物体表面之后，我们分成了几个部分：

• 折射部分，指的是被吸收到物体表面的那部分光线能量，具体表现出来就是物体的漫反射（Diffuse）
• 反射部分，指的是光线反射出来离开物体表面的那部分光照，具体指的就是镜面高光（Specular）

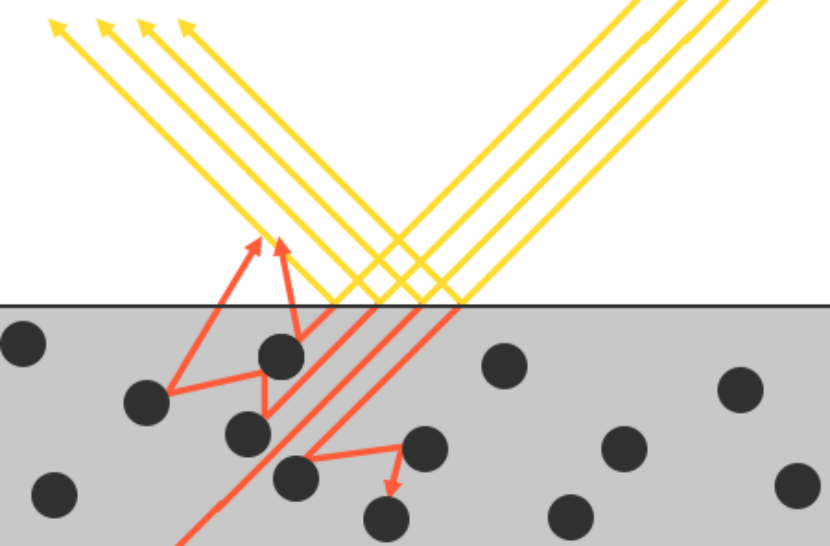
对于非金属物质来说，光线射进物体都会产生折射跟反射部分，而对于金属物质来说，微平面理论认为金属表面不会显示出漫反射部分，所有光线都会被处理成镜面高光
而能量守恒的要求，则是要求漫反射+高光部分占比加起来为1，实际实现中，我们往往先算出高光部分占比，然后在算出漫反射部分占比：

float kS = calculateSpecularComponent(); // 反射/镜面 部分
float kD = 1.0 - ks; // 折射/漫反射 部分

对比传统的Blinn-Phong模型，由于起没有考虑能量守恒，所以往往很难得出令人信服的效果

使用基于物理的BRDF

渲染方程(Render Equation)是用来模拟光的视觉效果最好的模型。而PBR的渲染方程是用以抽象地描述PBR光照计算过程的特化版本的渲染方程，被称为反射方程。
PBR的反射方程可抽象成下面的形式：

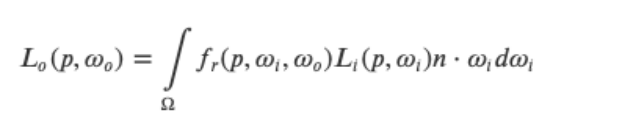
反射方程看似很复杂，但如果拆分各个部分加以解析，就可以揭开其神秘的面纱。

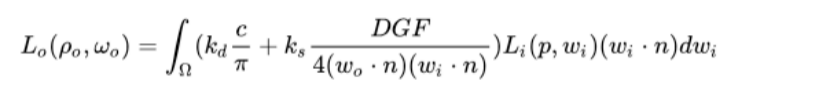
我知道这个公式不在说人话，所以把它翻译一下是这样的

1. 法线分布函数（Normal Distribution Function）：用于估算在收到表面粗糙度的影响下，取向方向与半程向量一致的微平面向量
2. 几何函数（Geometry Function）：用于描述微平面自成阴影的的函数，在表面粗糙度比较大的时候，平面上的微表面可能挡住了其他微表面的光线
3. 菲涅尔方程（Fresnel Rquation）：用于描述光线在不同的入射角度下表面反射光线所占的比率

以上每一种函数都描述了对应不同的物理现象，而实际渲染中，我们都会采用某种近似的函数，接下来我们来说下这几种近似函数的公式：
法线分布函数（Normal Distribution Function）的近似法线分布函数，从统计学上近似的表示了与某些（如中间）向量ℎ取向一致的微平面的比率。
目前有很多种NDF都可以从统计学上来估算微平面的总体取向度，只要给定一些粗糙度的参数以及一个我们马上将会要用到的参数Trowbridge-Reitz GGX（GGXTR）：

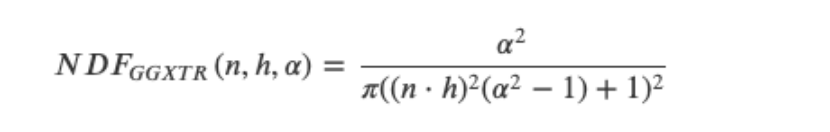
这里的h是用来测量微平面的半角向量，𝛼是表面的粗糙度，𝑛是表面法线。 如果将ℎ放到表面法线和光线方向之间，并使用不同的粗糙度作为参数，可以得到下面的效果：

成一个非常明亮的斑点。但是当表面比较粗糙的时候，微平面的取向方向会更加的随机，与向量ℎ取向一致的微平面分布在一个大得多的半径范围内，但是较低的集中性也会让最终效果显得更加灰暗。

使用glsl的实现则如下：

float DistributionGGX(vec3 N, vec3 H, float roughness)
{
   
   
  float a = roughness*roughness;
  float a2 = a*a;
  float NdotH = max(dot(N, H), 0.0);
  float NdotH2 = NdotH*NdotH;

  float nom   = a2;
  float denom = (NdotH2 * (a2 - 1.0) + 1.0);
  denom = PI * denom * denom;

  return saturateMediump(nom / denom);
}

几何函数（Geometry Function）的近似
几何函数模拟微平面相互遮挡导致光线的能量减少或丢失的现象。

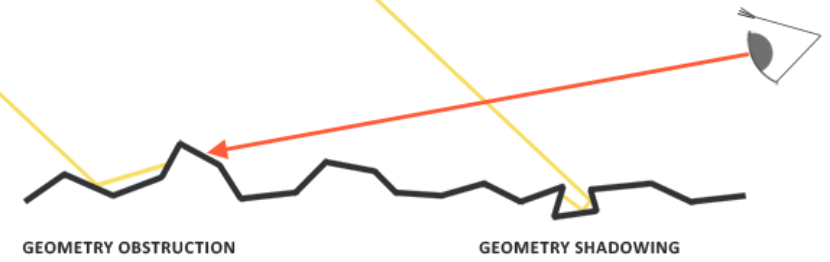
类似NDF，几何函数也使用粗糙度作为输入参数，更粗糙意味着微平面产生自阴影的概率更高。几何函数使用由GGX和Schlick-Beckmann组合而成的模拟函数Schlick-GGX：

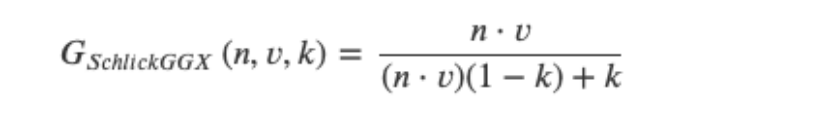
这里的𝑘是使用粗糙度𝛼计算而来的，用于直接光照和IBL光照的几何函数的参数：

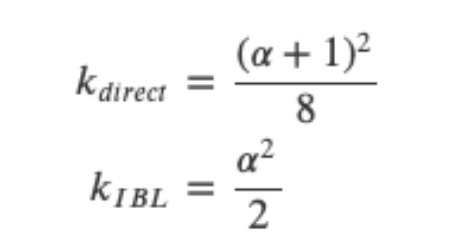
需要注意的是这里𝛼的值取决于你的引擎怎么将粗糙度转化成𝛼，在接下来的教程中我们将会进一步讨论如何和在什么地方进行这个转换。
为了有效地模拟几何体，我们需要同时考虑两个视角，视线方向（几何遮挡）跟光线方向（几何阴影），我们可以用Smith函数将两部分放到一起：

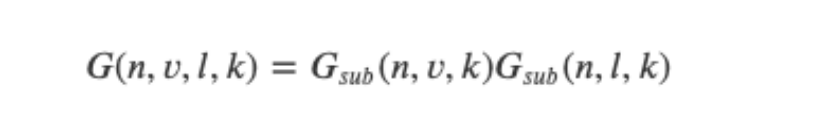
其中𝑣表示视线向量，𝐺𝑠𝑢𝑏(𝑛,𝑣,𝑘)表示视线方向的几何遮挡；𝑙表示光线向量，𝐺𝑠𝑢𝑏(𝑛,𝑙,𝑘)表示光线方向的几何阴影。使用Smith函数与Schlick-GGX作为𝐺𝑠𝑢𝑏Gsub可以得到如下所示不同粗糙度R的视觉效果：

几何函数是一个值域为[0.0, 1.0]的乘数，其中白色(1.0)表示没有微平面阴影，而黑色(0.0)则表示微平面彻底被遮蔽。
使用GLSL编写的几何函数代码如下：

float GeometrySchlickGGX(float NdotV, float k)
{
   
   
    float nom   = NdotV;
    float denom = NdotV * (1.0 - k) + k;
	
    return nom / denom;
}
  
float GeometrySmith(vec3 N, vec3 V, vec3 L, float k)
{
   
   
    float NdotV = max(dot(N, V), 0.0);
    float NdotL = max(dot(N, L), 0.0);
    float ggx1 = GeometrySchlickGGX(NdotV, k); // 视线方向的几何遮挡
    float ggx2 = GeometrySchlickGGX(NdotL, k); // 光线方向的几何阴影
	
    return ggx1 * ggx2;
}

菲涅尔方程（Fresnel Rquation）的近似

菲涅尔方程描述了光线被反射部分的比率，因而会受到观察方向的影响，结合能量守恒，我们可以得出剩下的漫反射的比率。而要计算出菲涅尔方程，我们需要一个基础反射率（F0）的参数，描述的是在表面的掠射角方向望过去（此时表面法线跟视线方向成90度），不同材料的表面反射率都不太一样：

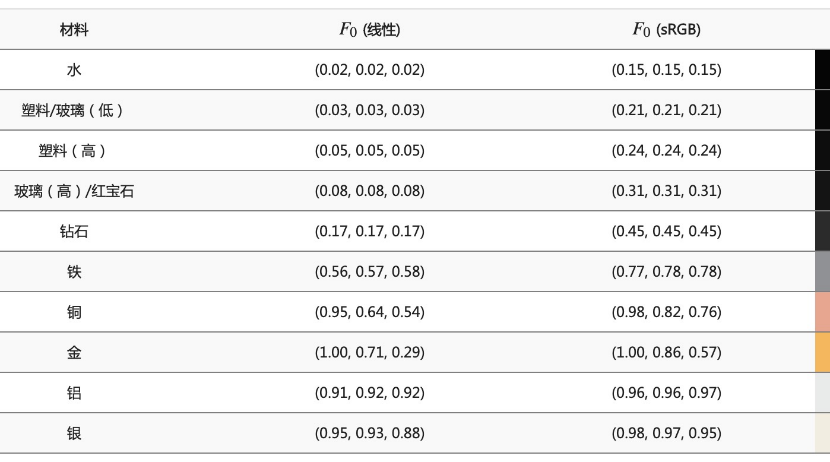
我们这里取0.04作为近似的基础反射率，另外，这里我们还需要额外引入一个叫做金属度（Metallic）的参数，结合F0，一般我们这样子来计算出材质的真实F0：

vec3 F0 = vec3(0.04);
F0 = mix(F0, albedo, metallic);

有了F0之后，我们使用Fresnel-Schlick近似来计算菲涅尔方程的近似：

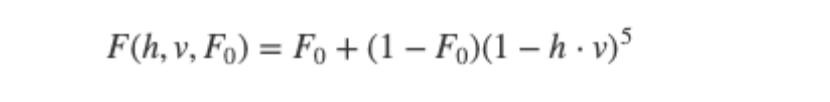
Fresnel Schlick近似可以用GLSL代码实现：

vec3 fresnelSchlick(float cosTheta, vec3 F0)
{
   
   
    return F0 + (1.0 - F0) * pow(1.0 - cosTheta, 5.0)