【数据结构】 图的邻接矩阵

在图的存储方法中，邻接矩阵通过数组对图的信息进行存储。

基本思路

使用邻接矩阵前，需要开一个一维数组数组，以存储各个顶点的数据（数组的编号与邻接矩阵中顶点的编号一一对应）；同时，还需要一个标记顶点是否被访问的一维数组，用来表示图中顶点是否被访问。【其中，标记顶点是否被访问的数组使用全局变量】

邻接矩阵为n*n方阵（二维数组），用来表示图中顶点间的连通关系（两顶点连通，数组值为1；两顶点不连通，数组值为0）。因此邻接矩阵edge数组的大小取决于图中顶点的数量。

邻接矩阵构造前，需要对标记数组、邻接矩阵edge数组分别进行初始化（赋值为0）。

构造邻接矩阵时，需要对应图中每条边的两端点，对邻接矩阵edge进行赋值（循环实现edge赋值时，循环变量的终止条件为边长）。

代码实现

本文邻接矩阵存储使用C++面向对象的方法实现。邻接矩阵本质上是数组，为静态存储，所以类中无需手动写析构函数，使用默认析构函数即可！

在类定义前，需要对数组长度进行统一分配

const int MaxSize=100;

类的声明

class MGraph{
public:
	MGraph(char a[],int n,int e);
	~MGraph(){};
	void dfs(int v);
	void bfs(int v);
private:
	char vertx[MaxSize];						//数组存储顶点数据
	int edge[MaxSize][MaxSize];					//邻接矩阵 
	int vertxNum,EdgeNum;		 				//记录顶点和边的数量 
};

类功能的实现

构造函数

以无向图为例，建立邻接矩阵。

构造函数所需参数分别为：顶点数据、定点数、边数。

构造过程及代码如下：

MGraph::MGraph(char a[],int n,int e){
	vertxNum=n,EdgeNum=e;						//1.顶点数、边数传入 
	int i,j,k;		
	for(i=0;i<vertxNum;i++) vertx[i]=a[i];		//2.顶点数组录入数据
				
	for(i=0;i<vertxNum;i++)						//3.初始化邻接矩阵 
		for(j=0;j<vertxNum;j++)
			edge[i][j]=0; 
	for(k=0;k<EdgeNum;k++){
        cout<<"输入相互邻接的顶点：";
		cin>>i>>j;								//4.输入邻接点编号，建图
		edge[i][j]=1;edge[j][i]=1; 
	}
}

图的遍历

图的遍历方式有两种，分别是DFS（深度优先）和BFS（广度优先），详情可以看笔者曾经发布的文章。在此不再赘述。

DFS算法过程及代码

void MGraph::dfs(int v){

	cout<<vertx[v];vis[v]=1;					//1.访问起点，并标记 
	for(int i=0;i<vertxNum;i++)			
	{
		if(edge[v][i]==1 && vis[i]==0) dfs(i);	
        					//2.从起点开始遍历未被访问的邻接点，直到将所有点遍历一遍为止
	}
} 

BFS算法过程及代码

void MGraph::bfs(int v){
	//bfs功能需要队列实现
	int rear,front,Q[MaxSize];
	front=rear=-1;								//1.建队列 
	int i,k;
	cout<<vertx[v];vis[v]=1;Q[++rear]=v;		//2.访问起点，顶点下标入队 
	while( rear != front ){
		k=Q[++front];							//3.队头出队，接下来遍历对头的邻接点 
		for(i=0;i<vertxNum;i++){
			if( edge[k][i]==1 && vis[i]==0 ) {
				cout<<vertx[i];vis[i]=1;Q[++rear]=i;
			} 
		}
	} 
} 

完整代码

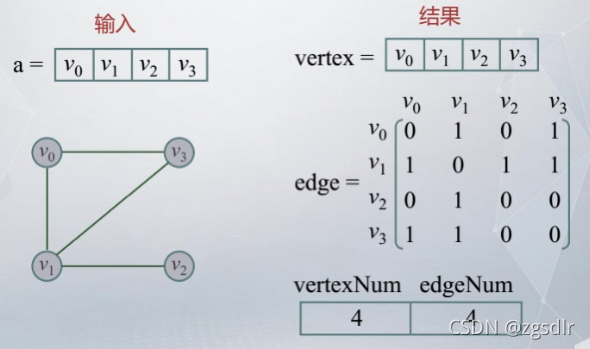
以无向图为例，测试的边为：(0 1) (0 2) (0 3) (0 4) (1 2) (2 4) 。

#include<iostream>
using namespace std;
const int MaxSize=100;
int vis[MaxSize];
class MGraph{
public:
	MGraph(char a[],int n,int e);
	~MGraph(){};
	void dfs(int v);
	void bfs(int v);
private:
	char vertx[MaxSize];						//数组存储顶点数据
	int edge[MaxSize][MaxSize];					//邻接矩阵 
	int vertxNum,EdgeNum;		 				//记录顶点和边的数量 
};

MGraph::MGraph(char a[],int n,int e){
	vertxNum=n,EdgeNum=e;						//顶点数、边数传入 
	int i,j,k;		
	for(i=0;i<vertxNum;i++) vertx[i]=a[i];		//顶点数组录入数据
				
	for(i=0;i<vertxNum;i++)						//初始化邻接矩阵 
		for(j=0;j<vertxNum;j++)
			edge[i][j]=0; 
	for(k=0;k<EdgeNum;k++){
        cout<<"输入相互邻接的顶点：";
		cin>>i>>j;		//输入邻接点编号，更新邻接矩阵
		edge[i][j]=1;edge[j][i]=1; 
	}
}

void MGraph::dfs(int v){

	cout<<vertx[v];vis[v]=1;					//访问起点，并标记 
	for(int i=0;i<vertxNum;i++)			
	{
		if(edge[v][i]==1 && vis[i]==0) dfs(i);	//从当前点开始遍历未被访问的邻接点 
	}
} 

void MGraph::bfs(int v){
	//bfs功能需要队列实现
	int rear,front,Q[MaxSize];
	front=rear=-1;								//1.建队列 
	int i,k;
	cout<<vertx[v];vis[v]=1;Q[++rear]=v;		//2.访问起点，顶点下标入队 
	while( rear != front ){
		k=Q[++front];							//3.队头出队，接下来遍历对头的邻接点 
		for(i=0;i<vertxNum;i++){
			if( edge[k][i]==1 && vis[i]==0 ) {
				cout<<vertx[i];vis[i]=1;Q[++rear]=i;
			} 
		}
	} 
} 


int main(){
	int n,e;
	cout<<"输入顶点数和边数：";
	cin>>n>>e;
	cout<<"输入顶点数据："; 
	char vt[MaxSize];
	for(int i=0;i<n;i++) cin>>vt[i];
	MGraph Gra(vt,n,e);			//建图
	
	cout<<"DFS:";
	for(int j=0;j<n;j++) vis[j]=0;	//初始化标记数组 
	Gra.dfs(0);						//dfs
	cout<<endl;
	
	cout<<"BFS:";
	for(int j=0;j<n;j++) vis[j]=0;	//初始化标记数组 
	Gra.bfs(0);								//bfs 
	cout<<endl;
	return 0;
}