堆（python实现，伪代码）

最新推荐文章于 2025-05-03 23:55:02 发布

zeronose

最新推荐文章于 2025-05-03 23:55:02 发布

阅读量616

点赞数

CC 4.0 BY-SA版权

分类专栏：算法与数据结构文章标签：数据结构算法 python

本文链接：https://blog.youkuaiyun.com/zeronose/article/details/123342561

算法与数据结构专栏收录该内容

23 篇文章

订阅专栏

这篇博客介绍了如何使用数组实现完全二叉树，并构建大根堆。内容包括堆的插入操作、最大值删除以及堆的下沉过程。通过`heapInsert`、`pop`和`heapify`等方法，确保了堆的性质得以维持。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

在这里插入图片描述
完全二叉树，上面层都是满的，不满的层也是从左到右要变满的
结点计算:

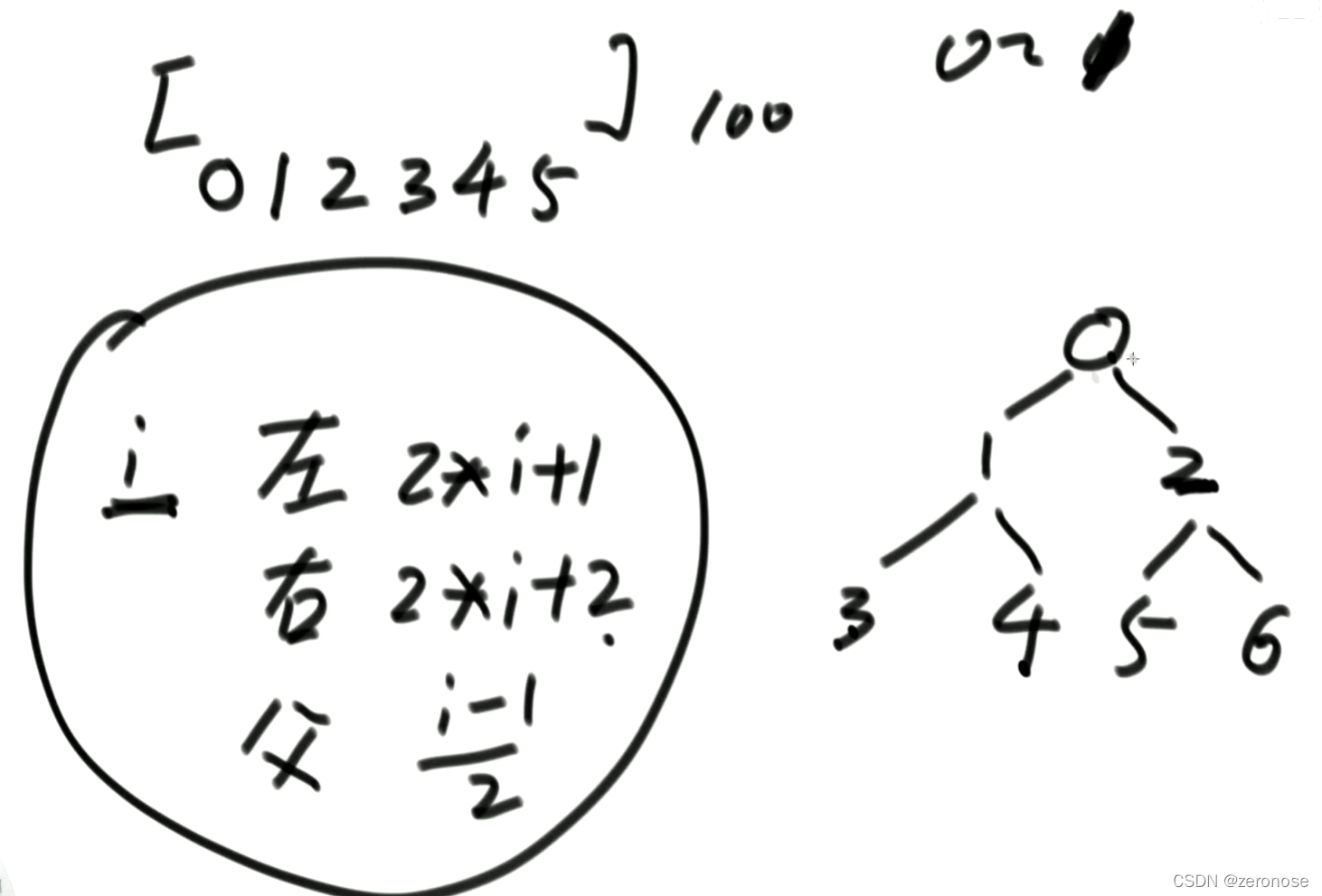
1.计算结点时是向下取整
2.只有头结点的父结点是自己

class Heap:
    # 堆就是用数组实现完全二叉树
    # 1.大根堆
    def put(self,arr, value, limit, heap_size=0):
        if heap_size == limit:
            print('堆满了')
        heap = arr
        heap[heap_size] = value
        heap_size += 1
        self.heapInsert(heap, heap_size)

    def heapInsert(self, arr, index):
        while arr[index] > arr[(index-1) /2]:
            self.swap(arr, index, (index-1)/2)
            index = (index-1)/2

    # 用户让你返回最大值，并且在大根堆中，把最大值删掉
    # 剩下的数，依然保持大根堆组织
    def pop(self, heap_size):
        ans = help[0]
        heap_size -= 1
        self.swap(help, 0, heap_size)
        self.heapify(heap, 0, heap_size)
        return ans

    # 从index位置往下看，不断的下沉
    # 停：我的孩子都不再比我大；已经没孩子了
    def heapify(self, arr, index, heap_size):
        left = index * 2 + 1
        while left < heap_size:
            # 左右两个孩子中，谁大，谁把自己的下标给largest
            # 右 -> 1)有右孩子 && 2）右孩子的值比左孩子大才行
            # 否则，左
            largest = left + 1 < heap_size and left + 1 if arr[left + 1]>arr[left] else left
            largest = largest if arr[largest] > arr[index] else index
            if largest == index:
                break
            self.swap(arr, largest, index)
            index = largest
            left = index * 2 + 1

    def swap(self, arr, i, j):
        temp = arr[i]
        arr[i] = arr[j]
        arr[j] = temp