最小二乘法构建线性回归方程

一、线性回归的意义

线性回归是利用数理统计中回归分析，来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法，运用十分广泛。在线性回归中，数据使用线性预测函数来建模，并且未知的模型参数也是通过数据来估计。由于市场现象一般是受多种因素的影响，而并不是仅仅受一个因素的影响。所以应用一元线性回归分析预测法，必须对影响市场现象的多种因素做全面分析。只有当诸多的影响因素中，确实存在一个对因变量影响作用明显高于其他因素的变量，才能将它作为自变量，应用一元相关回归分析市场预测法进行预测。
一元线性回归分析法的预测模型如下：

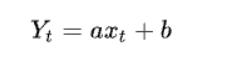
式中，x_t代表t期自变量的值；
Y_t代表t期因变量的值；
a、b代表一元线性回归方程的参数。
a、b参数由下列公式求得：

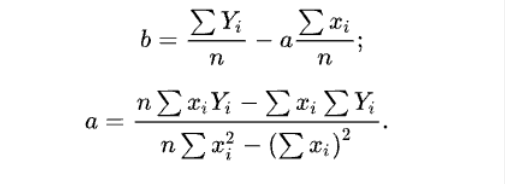
相关系数R²是用以反映变量之间相关关系密切程度的统计指标。我们可以用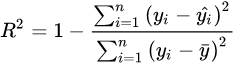
来刻画回归的效果。对于已经获取的样本数据，R²表达式中的总体平方和

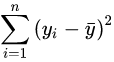
为确定的数。因此R²越大，意味着残差平方和