一、位图
问题:现有40亿无符号整数,需要从中查找一个指定的无符号整数是否存在,你要怎么解决?
解法一:遍历这些数据(效率低O(N));
解法二:先排序再二分查找(O(N*logN)+O(logN)),看似可行,实则不然:首先先要存放这些整数,一个整数4个字节,总共160亿字节,约为16G的内存,显然不行;
解法三:使用位图
###位图的原理:
将数据映射到bit位,这个bit位为1表示存在反之不存在;
template<size_t N>//非类型模板参数
class bitset
{
public:
bitset()
{
//给出整形空间,例如N=100,给出4个整形空间
_bs.resize(N / 32 + 1);
}
void set(size_t num)//将数据的存放的位置的比特位数值置为1,表示存在这个数据
{
int i = num / 32;
int j = num % 32;
_bs[i] |= (1 << j);
}
void reset(size_t num)//将数据存放的位置的那个比特位置为0,表示数值不存在
{
int i = num / 32;
int j = num % 32;
_bs[i] &= (~(1 << j));//逻辑:首先将1左移j位让表示 num 这个数据的比特位为1,再取反这个比特位为0,表示数据不存在
}
bool test(size_t num)//检测数据映射的比特位的数值来判断这个数据存在与否
{
int i = num / 32;
int j = num % 32;
return _bs[i] & (1 << j);
}
private:
vector<int> _bs;
};
就算是40亿个不重复的无符号整数,只需要40亿个比特位来映射,也就是4G左右;
###测试
void test1()
{
bitset<100> bs;//开了四个整形
bs.set(32);//映射到第一个整形空间中
cout << bs.test(32) << endl;
bs.reset(32);
cout << bs.test(32) << endl;
bs.set(122);
cout << bs.test(122) << endl;
bs.reset(122);
cout << bs.test(122) << endl;
bitset<-1> bs2;//开最大的即2^32-1
bs2.set(10000);
cout << bs2.test(10000) << endl;
}

使用库中的位图并不能开2^32个字节,因为库中底层是一个静态数组;而这里底层是vector存放的空间在堆区,空间很大。
问题二:要100亿个无符号整数,要从中选出只出现一次的数字;
解决方案:用两个比特位来表示一个数存在几次,00表示不存在,01表示出现1次,,10表示出现2次,11表示出现3次及其以上;为了有两个比特位,这里用一个类封装两个位图类;
template<size_t N>
class twobitset
{
public:
void set(size_t num)
{
bool bit1 = _bs1.test(num);
bool bit2 = _bs2.test(num);
if (!bit1 && !bit2)//00->01
{
_bs2.set(num);
}
else if (!bit1 && bit2)//01->10
{
_bs1.set(num);
_bs2.reset(num);
}
else if (bit1 && !bit2)//10->11
{
_bs2.set(num);
}
}
int get_count(size_t num)
{
bool bit1 = _bs1.test(num);
bool bit2 = _bs2.test(num);
if (!bit1 && !bit2)
{
return 0;
}
else if (!bit1 && bit2)
{
return 1;
}
else if (bit1 && !bit2)
{
return 2;
}
else
{
return 3;
}
}
private:
bitset<N> _bs1;
bitset<N> _bs2;
};
测试:
void test2()
{
twobitset<100> tbs;
int arr[] = { 1,1,1,2,2,3,4,4,4,5,5,6,7,7,7,8,8,9,98,99,100 };
for (auto i : arr)
{
tbs.set(i);
}
for (int i=0;i<100;i++)
{
if(tbs.get_count(i))
cout << i << "->" << tbs.get_count(i) << endl;
}
}

二、布隆过滤器
布隆过滤器的作用和位图一样,但是作用对象不同,布隆过滤器可以作用于字符串等等;这就需要我们提供哈希函数,将字符串转为无符号整型;
但是从哈希封装部分得知,不同的字符串可能对应的无符号整数值是一样的,这个时候就会出现哈希冲突;为了尽量减少哈希冲突,我们将一个字符串分别用多个不同的哈希函数映射多个不同的无符号值,再用这些无符号值映射到位图中,标记这个字符串存在与否;这种操作只能降低哈希冲突,但是不能完全避免;
哈希冲突会造成误判:就比在这里用三个哈希函数给每个字符串三个值,那么不同的两个字符串分别占有三个不同的位置,假设字符串1占有0、1、2,字符串2占有3、4、5,这个时候有另外一个字符串3要来映射,这个字符串会占有2,3,4;但是实际是就算没有set这个字符串3,在test检测有无字符串3时也会显示有,因为哈希冲突,字符串1、2已经将字符串3的位置占了;
所以只能用没有来判断不存在,不能用有判断存在(可能误判);
布隆过滤器没有支持reset,这也是会改变其他字符传的占位的情况造成的;
#include<iostream>
#include<vector>
using namespace std;
template<size_t N>//非类型模板参数
class bitset
{
public:
bitset()
{
//给出整形空间,例如N=100,给出4个整形空间
_bs.resize(N / 32 + 1);
}
void set(size_t num)//将数据的存放的位置的比特位数值置为1,表示存在这个数据
{
int i = num / 32;
int j = num % 32;
_bs[i] |= (1 << j);
}
void reset(size_t num)//将数据存放的位置的那个比特位置为0,表示数值不存在
{
int i = num / 32;
int j = num % 32;
_bs[i] &= (~(1 << j));//逻辑:首先将1左移j位让表示 num 这个数据的比特位为1,再取反这个比特位为0,表示数据不存在
}
bool test(size_t num)//检测数据映射的比特位的数值来判断这个数据存在与否
{
int i = num / 32;
int j = num % 32;
return _bs[i] & (1 << j);
}
private:
vector<int> _bs;
};
//哈希转整形的函数
// BKDR 哈希类模板
template<typename K >
class BKDRHash {
public:
size_t operator()(const K& str) const {
size_t seed = 131; // 31 131 1313 13131 131313 etc..
size_t hash = 0;
for (char c : str) {
hash = (hash * seed) + c;
}
return hash;
}
};
// DJB2 哈希类模板
template<typename K >
class DJB2Hash {
public:
size_t operator()(const K& str) const {
size_t hash = 5381;
for (char c : str) {
hash = ((hash << 5) + hash) + c; // 等价于 hash * 33 + c
}
return hash;
}
};
// AP Hash Function
#include <string>
// APHash 类模板
template<typename K >
class APHash {
public:
size_t operator()(const K& str) const {
size_t hash = 0xAAAAAAAA;
for (size_t i = 0; i < str.length(); ++i) {
if ((i & 1) == 0) {
hash ^= ((hash << 7) ^ str[i] * (hash >> 3));
}
else {
hash ^= (~((hash << 11) + (str[i] ^ (hash >> 5))));
}
}
return hash;
}
};
template<size_t N, size_t X=5, class K=std::string ,
class Hash1= BKDRHash<K>,class Hash2= DJB2Hash<K>,class Hash3= APHash<K>>
class bloomfliter
{
public:
void Set(const K& key)
{
unsigned int hash1 = Hash1()(key) % M;
unsigned int hash2 = Hash2()(key) % M;
unsigned int hash3 = Hash3()(key) % M;
_bs.set(hash1);
_bs.set(hash2);
_bs.set(hash3);
}
bool Test(const K& key)
{
unsigned int hash1 = Hash1()(key) % M;
unsigned int hash2 = Hash2()(key) % M;
unsigned int hash3 = Hash3()(key) % M;
if (!_bs.test(hash1) || !_bs.test(hash2) || !_bs.test(hash3))
return false;//有一个映射的位置为0就说明没有这个值
return true;
}
private:
static const int M = N * X;//哈希表的长度
bitset<N * X> _bs;
};
#include"BloomFliter.h"
int main()
{
bloomfliter<10> _bf;
_bf.Set("孙悟空");
_bf.Set("猪八戒");
_bf.Set("唐僧");
cout << _bf.Test("孙悟空") << endl;
cout << _bf.Test("猪八戒") << endl;
cout << _bf.Test("唐僧") << endl;
cout << _bf.Test("白龙马") << endl;
cout << _bf.Test("沙僧") << endl;
return 0;
}

M是哈希表的长度,X是一个定值,N是数据个数 ;当N增大时,,M减少,此时误判率会增加,反之减少。
三、海量数据处理
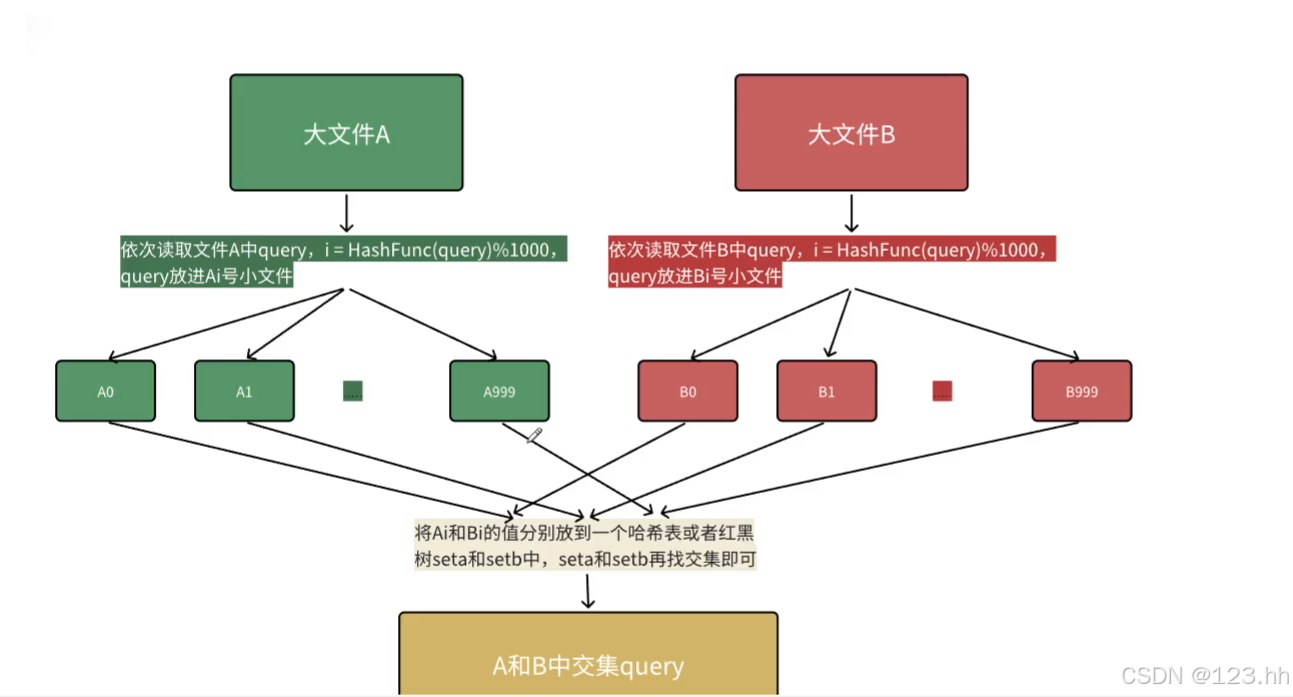
问题一:先有两个个500G的大文件,要寻找这两个文件之间相同的部分;我们知道文件中是以字符串的形式存储的,所以使用位图肯定不行,布隆过滤器可以;
这里有一种新的解决方案:将文件中所有query查询语句利用哈希函数将转为整形值再模上1000得到每个query语句的映射值;再给出000个小文件并且每个小文件依次编号,将query放进其映射值与文件编号相同的小文件;最后再将这些小文件的值依次放到set中,然后再对两个大文件的编号相同的小文件的set进行对比就能找到相同的部分;
由于只有相同的query才会放到相同编号的小文件,所以两个大文件在进行比较时,只需要比较两者编号相同的小文件;
当一个小文件太大时有两种情况:一是这个小文件中有许多相同的query,这种情况不需要处理,因为插入到set中会去重,最后得到的不会占用很多内存;第二种情况就是哈希冲突很多,有很多不同的query语句放到了相同的小文件中,此时放入set中内存会不够出现抛异常的情况,针对于这种情况,需要对这个小文件进行相同的映射分组比较操作;
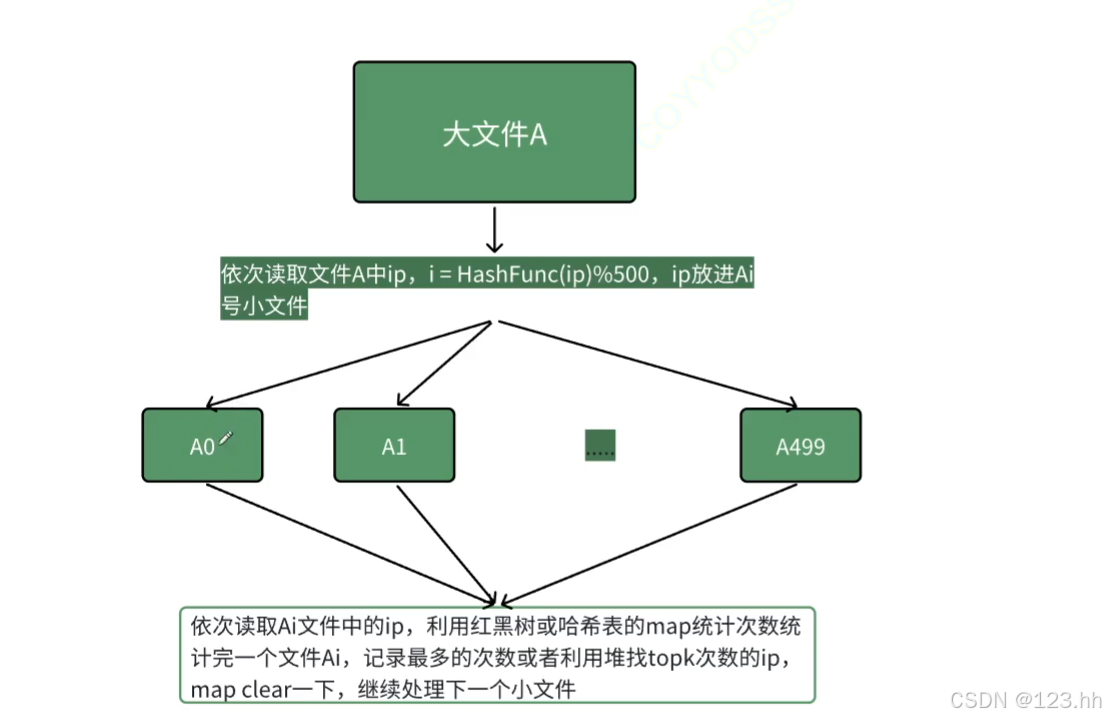
问题二:有100G的一个log file,如何寻找其中出现次数最多的ip地址?
解决方案:依次读取大文件中的ip值并转为整形模上分为的小文件个数,将相同的ip放到相同编号的小文件中;之后再读取小文件中的ip放到一个map<string,int>中int统计相同ip出现的个数,最后统计出现次数最多的ip就能找出了;
分为小文件的目的是因为大文件的体积太大无法放入内存中进行读取;
也会出现像问题一中出现的问题即小文件体积过大,对应的解决方式相同





















 1122
1122

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








