Guava包中的BloomFilter_guava bloomfilter-优快云博客

本文链接：https://blog.youkuaiyun.com/zc19921215/article/details/91047708

如果要判断某个元素是否存在的话，首先想到的都是将数据放入到一个HashSet中，然后判断元素是否存在。但是这个方法有一个缺点，即当数据量很大时，比如1亿个整数，所耗费的内存空间也很大。

优化方案一：使用BitSet

可以初始化一个很长的一个Bit数组，将数值对应的Bit位置为true，然后根据是true还是false判断对应位置的数值是否存在。例如现在有数值0、3、63，我们可以初始化一个长度为64的Bit数组，将0、3、63置为true，然后通过get()方法查看对应位置的数值是否存在：

代码Demo如下：

但是BitSet有两个比较局限的地方：

第一是当样本分布极度不均匀的时候，BitSet会造成很大空间上的浪费。举个例子，比如你有5个数，分别是1、2、3、4、999，那么这个BitSet至少得有1000位，中间的位置很多就被浪费掉了。

第二是BitSet只面向数字比较，并且还得是正数，其他类型需要先转换成int类型，但是转换过程中难免会出现重复，BitSet的准确性就会降低。

针对以上两个问题，解决思路就是：

分布不均匀的情况可以通过hash函数，将元素都映射到一个区间范围内，减少大段区间闲置造成的浪费。然后可以把其他类型映射成整数，映射时可以多hash几次同时扩大数组的范围，减少hash冲突的概率。

基于这种思想，Bloom Filter(布隆过滤器)诞生了，个人感觉Bloom Filter就是加强版的BitSet。

什么是Bloom Filter(布隆过滤器)？

Bloom Filter可以理解为是一个m位的数组，它有k个相互独立的哈希函数。每当新来一个元素时，会使用这些哈希函数分别计算，将对应位置置为1。查询时也要进行k次哈希运算，如果对应的k个位置都为1，则表明元素可能存在。代码Demo如下：

Bloom Filter示意图：

那么，m和k分别取多少比较合适呢？

这两个数值是通过公式推导出来的，具体推导过程可以看《数学之美》或者是本文参考中给出的链接，这边直接贴一下结论：

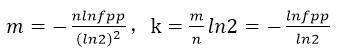
然后论文《Less Hashing, Same Performance: Building a Better Bloom Filter》又提出的一个技巧，可以用2个哈希函数来模拟k个哈希函数，即gi(x) = h1(x) + ih2(x) ，其中0<=i<=k-1；

我们分析下guava18.0包中提供的布隆过滤器的源码，大概了解下布隆过滤器内部的运行原理。

Guava包中的布隆过滤器分析：

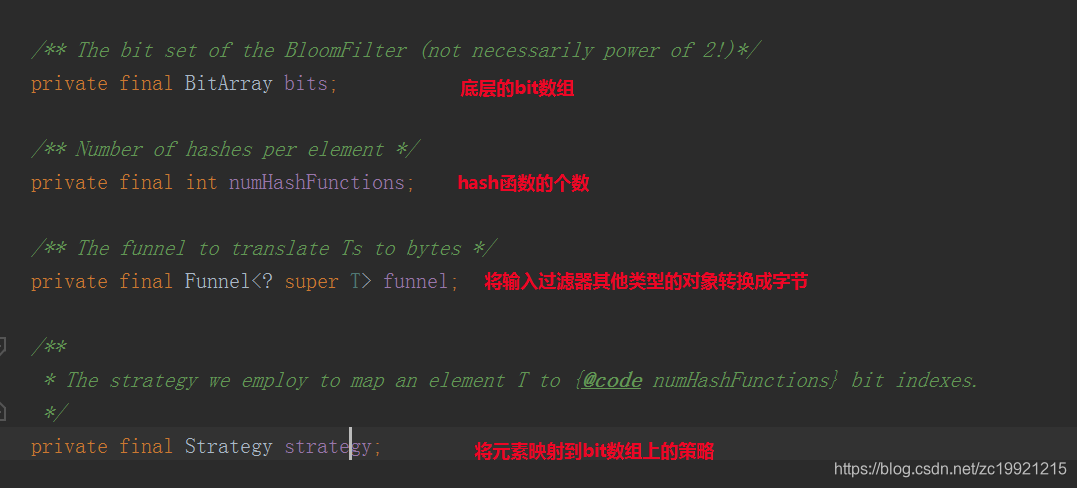
Funnel：

Funnel是Guava中定义的一个接口，它和PrimitiveSink配套使用，主要是把任意类型的数据转化成HashCode (byte数组)。Guava预定义了一些原生类型的Funnel，如String、Long、Integer等等。

Strategy：

它是一个内部接口，主要有put()和mightContain()两个方法，它们的作用分别是将元素放入布隆过滤器和判断元素在布隆过滤器中是否存在。

目前有两种策略：MURMUR128_MITZ_32 和 MURMUR128_MITZ_64，两者使用的都是MurmurHash3算法，个人理解两者的区别在于使用hash值的位数不同，前者使用了64位，后者是使用全部的128位，默认情况下使用的是后者。本文这里选取默认的Strategy进行分析。

put():

mightContain():

布隆过滤器无法支持元素的删除操作,但是Counting BloomFilter通过存储位元素每一位的置为1的数量，使得布隆过滤器可以支持删除操作，但是这样会数倍地增加布隆过滤器的存储空间。

参考：

《数学之美》

https://zh.wikipedia.org/zh-hans/Murmur%E5%93%88%E5%B8%8C(MurmurHash算法)