实数信号和复数信号的信噪比分析

一、电压电流信号与功率的转换

电压信号

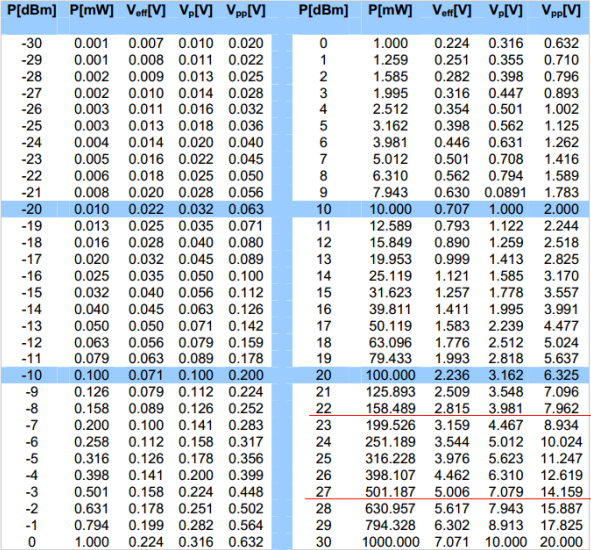
电压功率的换算关系式：

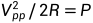
其中R为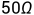的匹配阻抗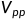，为峰值电流。

以1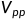的电压为例：

，

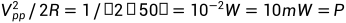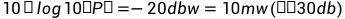
电流信号

电流功率的换算关系式：

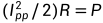
其中R为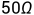的匹配阻抗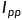，为峰值电流。

以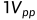即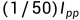的电压为例：

，

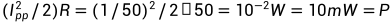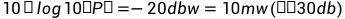
二、复信号的信噪比分析

对于复信号而言（假设噪声也是复数），信号频谱为单边谱，经过FFT之后，信号幅度增加N倍，噪声幅度增加倍，信噪比增加N倍。

clear all;
clc;
close all;
f = 10;
Fs = 40;
L = 1000;
t = (0:L-1)/Fs;
f_1 = Fs*(0:(L-1))/L;
index = find(abs(f-f_1) == min(abs(f-f_1)));
amp_signal_db = (10 - 30 - 14)/2 ;                              % 10dbm

signal = (10.^(amp_signal_db/10))*exp(1j*2*pi*f*t);             % 电流

noise_R_db = (-20 - 30 - 14 + 10*log10(Fs/2))/2;                % -20dbm

noise_R = 10.^(noise_R_db/10);
noise = ((noise_R + 1j*noise_R)*(randn(1,L)));

SNR_INITIAL = 10 - (-20 + 10*log10(Fs/2));

figure;
Xresum =  signal + noise;
n1=length(Xresum);
FFTXresum = fft(Xresum,n1)/(n1);
PowXresum2 = abs(FFTXresum);

PowXresum_one_r = PowXresum2(1:n1/2+1);

PowXresum_one = (PowXresum_one_r(2:end));
PowXresum_one = 20*log10(PowXresum_one) + 14 + 30;
f1 = Fs*(1:(n1/2))/n1;
noise_floor_plot1 = round((mean(PowXresum_one(50:200)))*10)/10;
signal_power = PowXresum_one(index-1);

SNR_end = signal_power - (noise_floor_plot1);

plot(f1,PowXresum_one);
title('单路接收信号频谱图','FontSize',13);
xlabel('频率/GHz','FontSize',13);
ylabel('功率/dBm','FontSize',13);

假设信号的功率谱密度为10dbm，因为是单音信号所以信号功率也为10dbm。对于电流信号，已知功率P(mw)，则电流，换算成db为单位

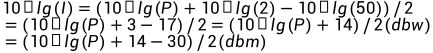
理论分析：

因为噪声增加了倍(N为采样点个数)。而我们做完FFT之后除了N，所以噪声功率降低了N倍，信号功率不变，所以信噪比增加N倍。实际上，FFT之后的噪声功率 = 噪声的功率谱密度*RBW。其中。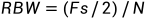

实验分析：

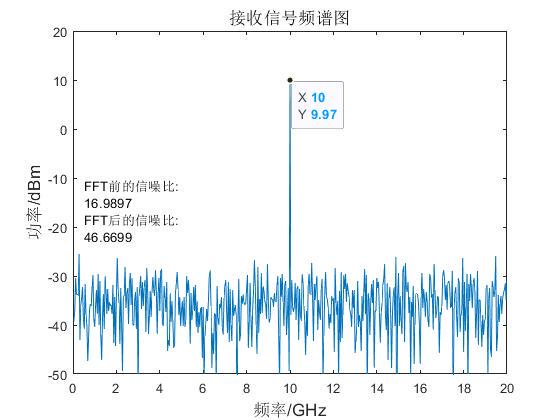
实验中设置信号的幅度为10dbm，与FFT之后的功率谱相对应。而FFT前后的信噪比增加了约30db。30db = 10*log10(N) = 10*log10(1000)，与理论分析一致。

三、实信号的信噪比分析

对于实信号而言，因为经过FFT之后频谱为双边谱，单音实信号的幅度为单音复信号的1/2。要恢复原来信号的幅度应该除以(N/2)。对于噪声来说，情况就比较复杂。以高斯随机噪声为例，因为噪声的幅度是一个随机值，所以一般是功率除以(N/2)。可通过matlab进行验证。

clear all;
clc;
close all;
f = 10;
Fs = 40;
L = 1000;
t = (0:L-1)/Fs;
% noise_R = 1;
noise_R = 1 + 1j;
noise = ((noise_R)*(randn(1,L)));
figure;
Xresum = noise;
n1=length(Xresum);
FFTXresum = fft(Xresum,n1)/(sqrt(n1));
PowXresum_one = abs(FFTXresum);

f1 = Fs*(0:(n1-1))/n1;
noise_floor_plot1 = round((mean(PowXresum_one(50:200)))*10)/10;

plot(f1,PowXresum_one);
title('接收信号频谱图','FontSize',13);
xlabel('频率/GHz','FontSize',13);
ylabel('功率/dBm','FontSize',13);
ylim([-50,20]);

对于复数噪声，其幅值为实数噪声的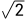倍。因此要和复数噪声一样保持其FFT之后的幅度不变就需要除以。

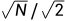复信号噪声功率：

实信号噪声功率：

基于以上分析，我们对fft之后实信号的信噪比进行分析。

clear all;
clc;
close all;
f = 10;
Fs = 40;
L = 1000;
t = (0:L-1)/Fs;
f_1 = Fs*(0:(L-1))/L;
index = find(abs(f-f_1) == min(abs(f-f_1)));
amp_signal_db = (10 - 30 - 14)/2 + 3;                             % 10dbm，除2之后加3db，是因为幅度加3db

signal = (10.^(amp_signal_db/10))*sin(2*pi*f*t);
noise_R_db = (-20 - 30 - 14 + 3 + 10*log10(Fs/2))/2;             % -20dbm, 因为是双边谱，所以加了3db，功率加3db相当于幅度乘以根号2
noise_R = 10.^(noise_R_db/10);
noise = ((noise_R)*(randn(1,L)));
SNR_INITIAL = 10 - (-20 + 10*log10(Fs/2));

figure;
Xresum =  signal + noise;
n1=length(Xresum);
FFTXresum = fft(Xresum,n1)/(n1);
PowXresum2 = abs(FFTXresum);

PowXresum_one_r = PowXresum2(1:n1/2+1);

PowXresum_one = (PowXresum_one_r(2:end));
PowXresum_one = 20*log10(PowXresum_one) + 14 + 30;
f1 = Fs*(1:(n1/2))/n1;
noise_floor_plot1 = round((mean(PowXresum_one(50:200)))*10)/10;
signal_power = PowXresum_one(index-1);

SNR_end = signal_power - (noise_floor_plot1);

plot(f1,PowXresum_one);
title('接收信号功率谱','FontSize',13);
xlabel('频率/GHz','FontSize',13);
ylabel('功率/dBm','FontSize',13);
ylim([-50,20]);

str1 = 'FFT前的信噪比: ';
str2 = [num2str(SNR_INITIAL)];
str3 = 'FFT后的信噪比: ';
str4 = [num2str(SNR_end)];
str_SNR={str1,str2,str3,str4};
text(0.5,noise_floor_plot1+20,str_SNR);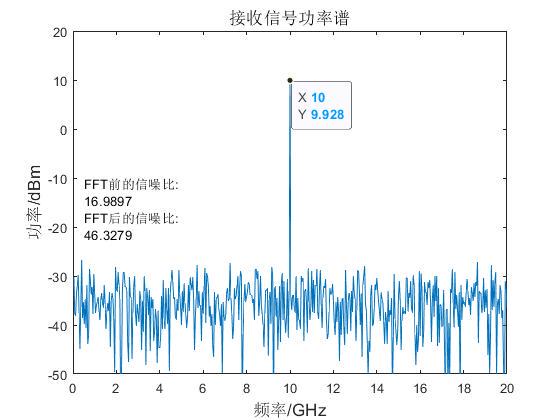

仿真结果如图，可以看到信号幅度保持不变，信噪比增加30db，和复信号的信噪比分析一致。

结论

针对上面的实验结果，可以得出以下几条结论：

1. 对于单音复信号，FFT之后除以N(采样点数)可以还原信号幅度，对于单音实信号，信号幅度*2（实信号幅度为复信号的一半），再经过FFT之后除以N也可以还原信号幅度。

2. 对于噪声信号，因为复信号的幅度是实信号幅度的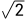倍，因此要还原噪声的幅度，需要在实信号的基础上乘以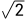，经过FFT之后除以。

3. 信号加上噪声之后经过FFT变化，信噪比提高N倍。