AVL二叉树

原创 已于 2025-11-26 23:05:02 修改 · 573 阅读 · 12 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#c++ #c语言 #后端

于 2025-11-26 22:18:26 首次发布

AVL二叉树

一. AVL树的概念

二叉树搜索的数据有序或接近有序时，搜索效率就会接近于n，效率低下。当向二叉搜索树中插入新结点后，如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整)，即可降低树的高度，从而减少平均搜索长度。
一棵AVL树或者是空树，或者是具有以下性质的二叉搜索树：

  1. 它的左右子树都是AVL树
  2. 左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1)
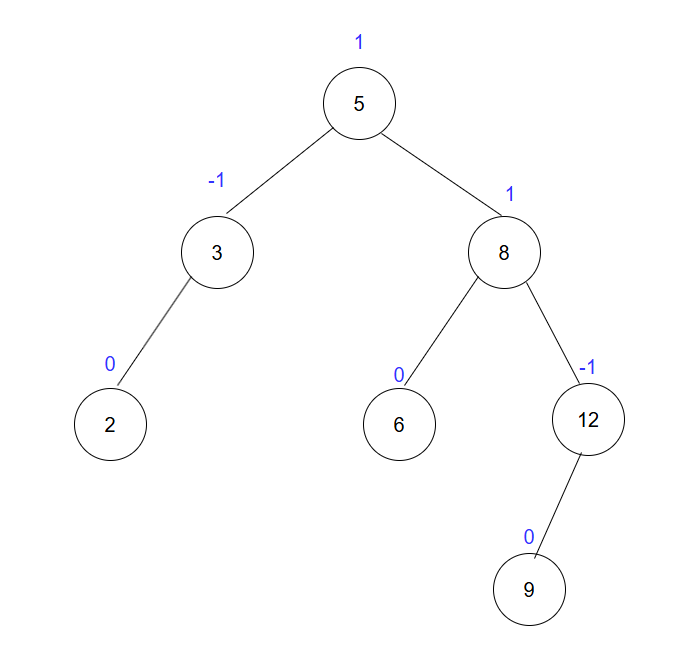
    在这里插入图片描述
    平衡因子规定左子树高度减右子树高度。

二. AVL树模拟实现

1. AVL树节点

template <class T ,class V>
struct AvlNode
{
	AvlNode<T,V>* _right;
	AvlNode<T,V>* _left;
	AvlNode<T,V>* _parent;//该节点的父节点
	std::pair<T, V> _kv;//kv形式存储数据
	int _bf;//平衡因子

	AvlNode(const std::pair<T,V>& kv)
		:_right(nullptr)
		,_left(nullptr)
		,_parent(nullptr)
		,_kv(kv)//自定义参数拷贝构造，调用它自己的拷贝函数。
		,_bf(0)
		{
		}
};

2. AVL树的整体

template <class T, class V>
class AVLStree
{
	typedef AvlNode<T, V> node;

public:


private:

	node* root = nullptr;
};

3. AVL树的插入

  1. 首先AVL树插入满足二叉搜索树：
    从根开始，根为空，直接在根上插入；根不为空，小于根节点的k值，往右寻找，大于往左找，按照该规则，直到找到一个为空的节点，在该位置插入。

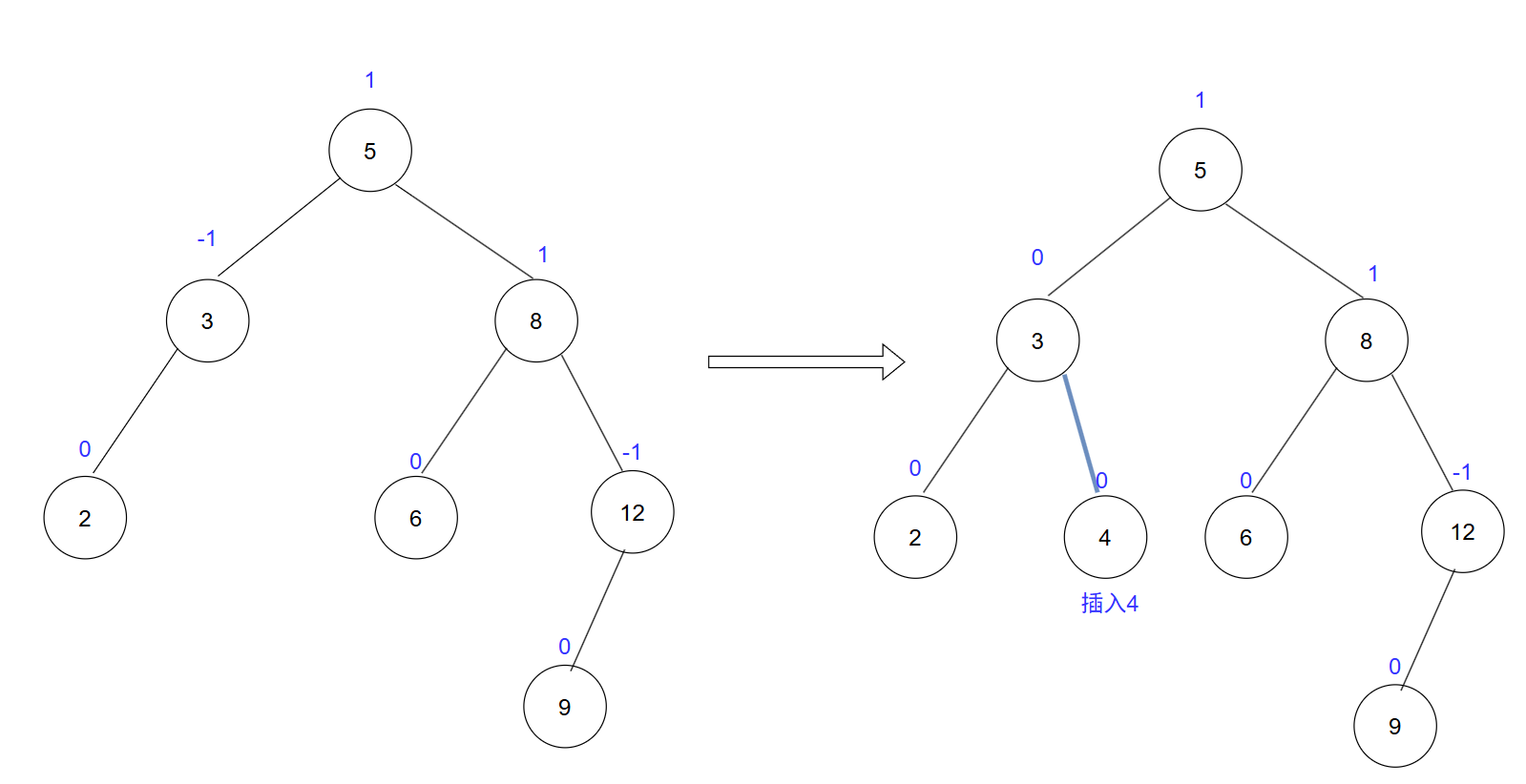
在这里插入图片描述

bool insert(const pair<T, V>& kv)
{
	if (_root == nullptr)//根为空，在根上插入
	{
		_root = new node(kv);
		return true;
	}
	
	node* cur = _root;
	node* parent = nullptr;
	while (cur)
	{
		if (cur->_kv.first == kv.first)
		{
			return false;
		}
		else if (kv.first < cur->_kv.first)
		{
			parent = cur;
			cur = cur->_left;
		}
		else if (kv.first > cur->_kv.first)
		{
			parent = cur;
			cur = cur->_right;
		}
	}//寻找插入位置
	if (kv.first<parent->_kv.first)
	{
		parent->_left = new node(kv);
	}
	else if (kv.first > parent->_kv.first)
	{
		parent->_right = new node(kv);
	}

}
  1. 插入后调整每个节点的平衡因子
while (parent)
{
	if (cur==parent->_right)//当该节点右子树高度增加了，平衡因子加一。
	{
		parent->_bf++;
	}
	else if (cur == parent->_left)//当该节点左子树高度增加了，平衡因子减一。
	{
		parent->_bf--;
	}

	if (parent->_bf == 0)//平衡因子为0，不用继续向上调节了。
		break;
	else if (parent->_bf == 1 || parent->_bf == -1)//平衡因子为1或-1，继续向上调整。
	{
		cur = parent;
		parent = parent->_parent;
	}
	else//平衡因子为2或-2，需要调节二叉树。
	{
		
	}

};

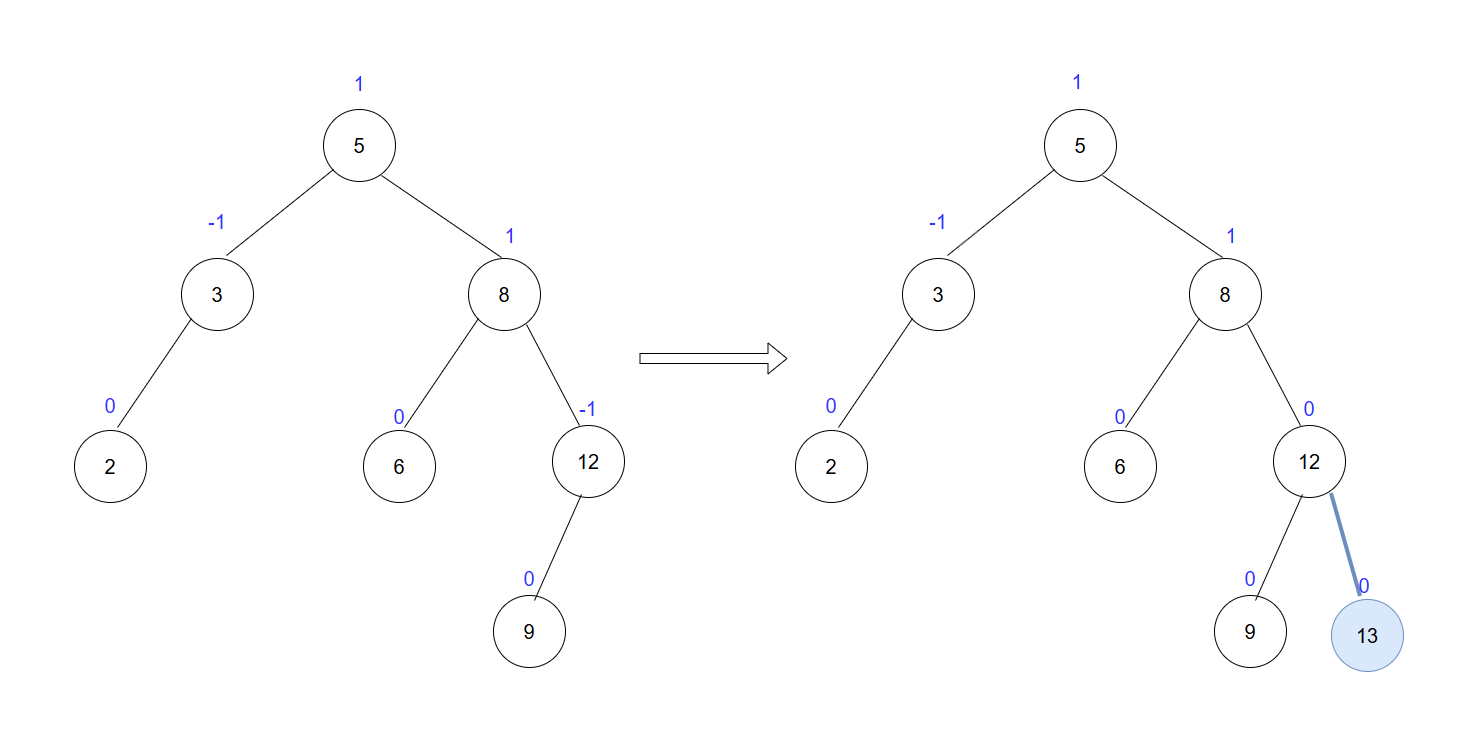
在这里插入图片描述
当该节点平衡因子为0，就不需要往上修改了，说明以该节点为根的子树，高度没有改变，为1或-1时，就继续向上修改。

  1. 旋转AVL树
    当二叉树的某节点平衡因子为2或-2时，需要旋转二叉树。
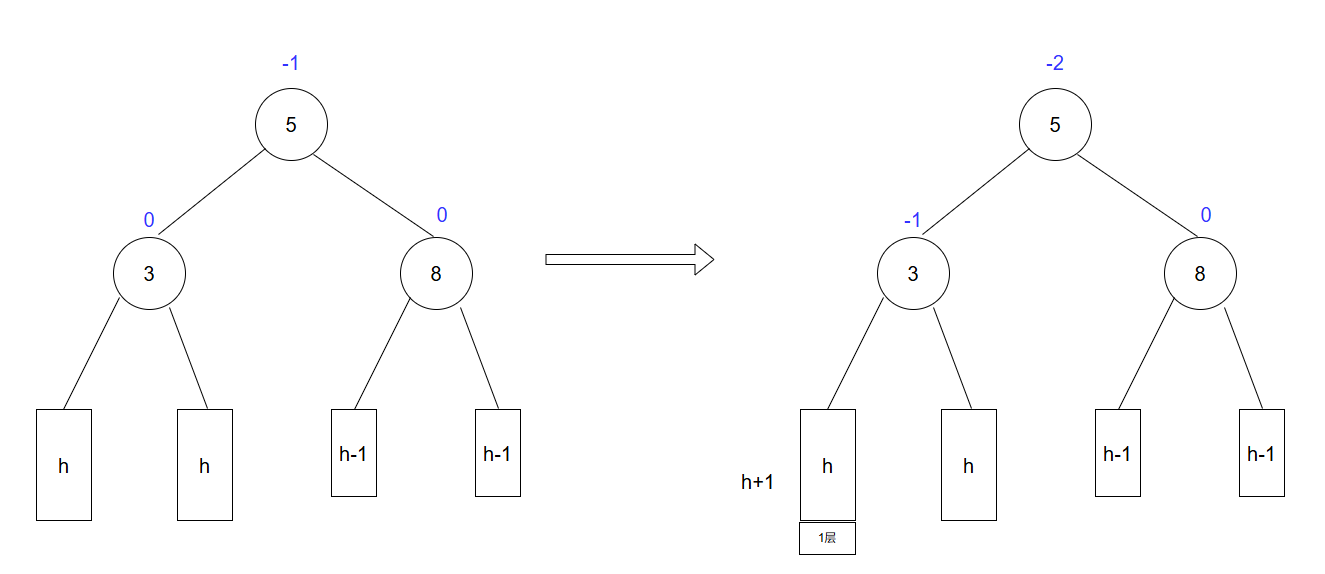
    在这里插入图片描述
    如图上这种情况，5节点的左孩子的左子树上插入1层，导致平衡因子变成了-2，可以采取右旋转。
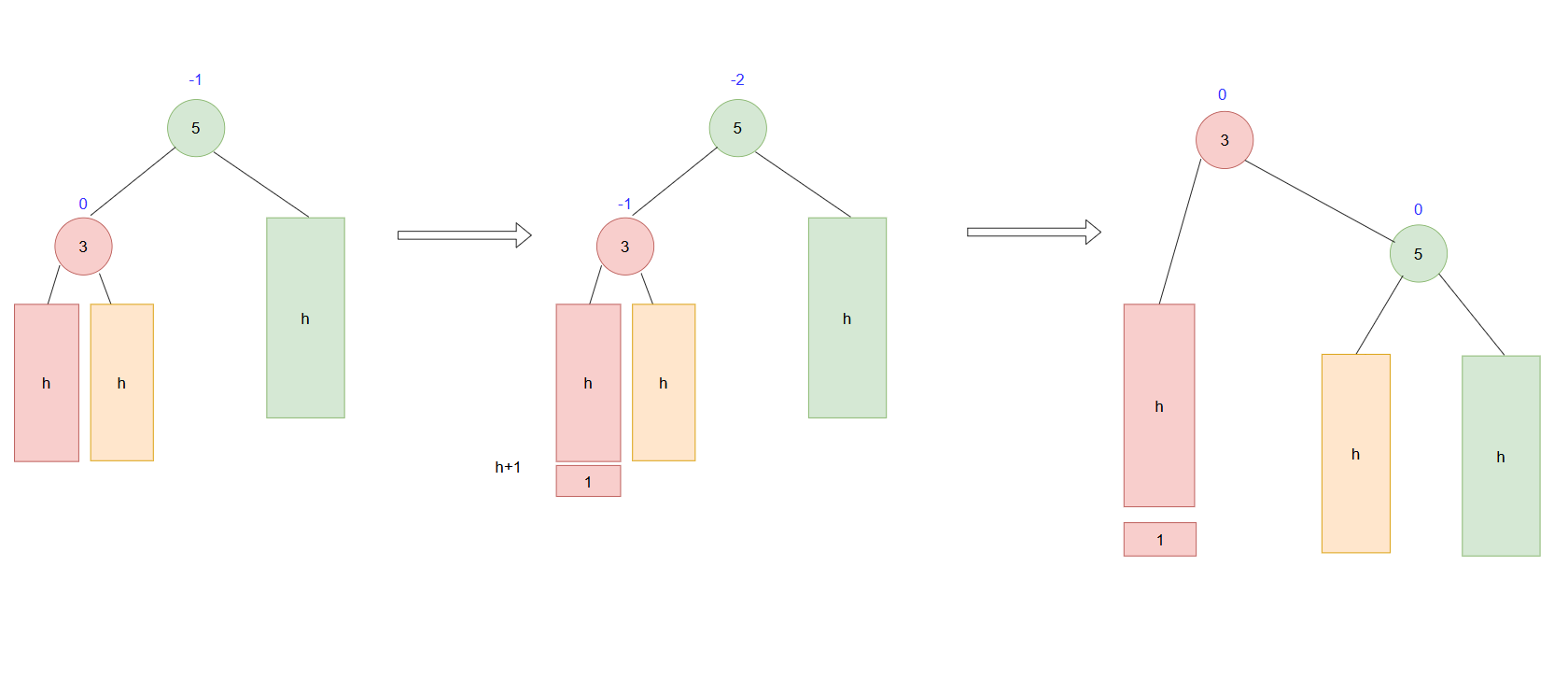
    在这里插入图片描述
    右旋就是将平衡因子为-2节点的左子树的右子树，成为-2节点的左子树，然后使-2节点，成为它原理左子节点的，右子树。（该旋转符合搜索二叉树排序规则）
    我们发现旋转后平衡因子改变的只有根和左子节点的，且都变成了0，其他子树的形状保持不变因此平衡因子未改变，且树的高度也未改变，都是h+2，因此该旋转数上面的节点的平衡因子不受影响。
void RotateR(node* root)
{
	node* cur = root->_left;//先拿到-2节点的左子节点
	root->_left = cur->_right;//根的左子树成为左子节点的右子树
	if(cur->_right)
	cur->_right->_parent = root;//左子节点的右子树的父亲改为根
	cur->_right = root;//让根成为左子树的右节点
	cur->_parent = root->_parent;//让左子树成为新的根节点
	if (root->_parent == nullptr)//判断该节点是否为_root
	{
		_root = cur;			//_root为原来的左子节点
		root->_parent = cur;
		root->_bf = 0;
		cur->_bf = 0;
		return;
	}
	else if (root->_parent->_left == root)
	{
		root->_parent->_left = cur;
	}
	else
	{
		root->_parent->_right = cur;
	}
	root->_parent = cur;//原来的根的父亲改为原来的左子节点
	root->_bf = 0;//将两个改变的平衡因子修改
	cur->_bf = 0;

}
  1. AVL树左旋
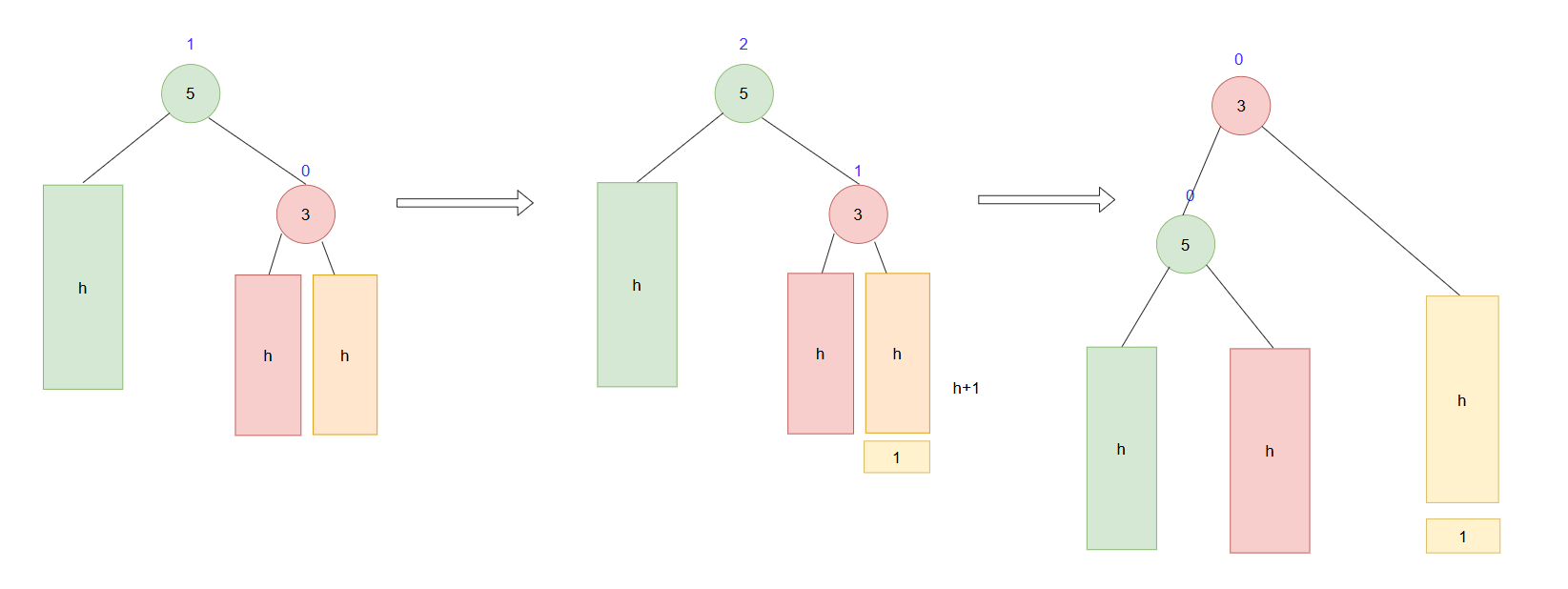
    上面讲了右旋，再来看左旋，左旋顾名思义，就是当树的右边插入数据导致平衡因子，超过了1或-1，从而向左边旋转的操作。
    左旋满足根平衡因子为2，右子节点平衡因子为1。
    在这里插入图片描述
void RotateL(node* root)
{
	node* cur = root->_right;//先拿到-2节点的右子节点
	root->_right = cur->_left;//
	if (cur->_left)
		cur->_left->_parent = root;//右子节点的右子树的父亲改为根
	cur->_left = root;//让根成为右子树的左节点
	cur->_parent = root->_parent;//让右子树成为新的根节点
	if (root->_parent == nullptr)//判断该节点是否为_root
	{
		_root = cur;			//_root改为原来的右子节点
		root->_parent = cur;
		root->_bf = 0;
		cur->_bf = 0;
		return;
	}
	else if (root->_parent->_left == root)
	{
		root->_parent->_left = cur;
	}
	else
	{
		root->_parent->_right = cur;
	}
	root->_parent = cur;//原来的根的父亲改为原来的右子节点
	root->_bf = 0;//将两个改变的平衡因子修改
	cur->_bf = 0;

}
  1. AVL树的左右旋转
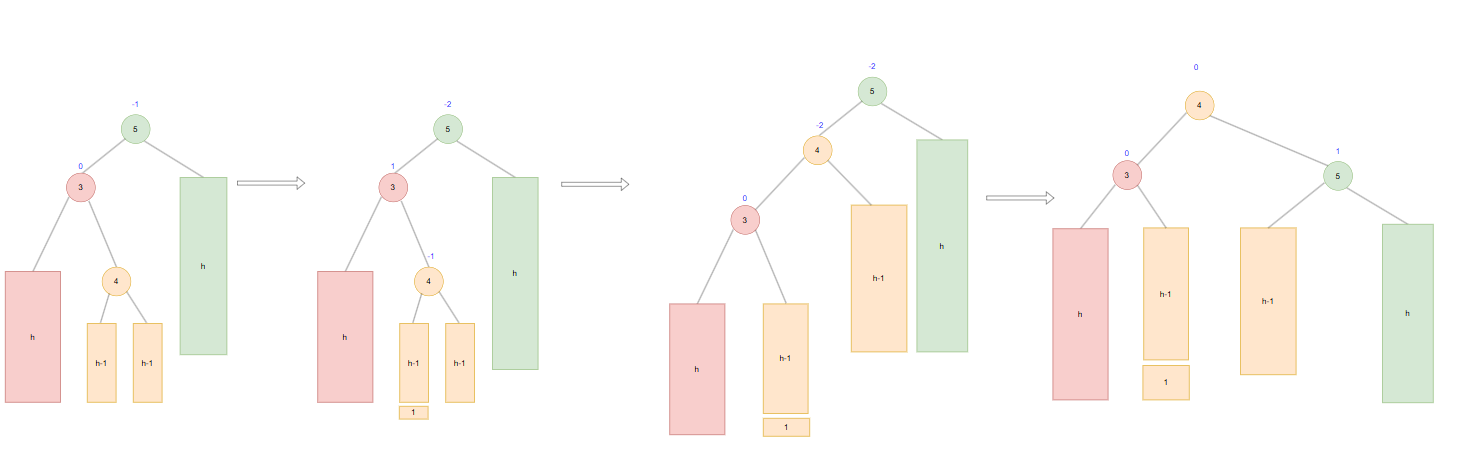
    在这里插入图片描述
    如图某节点平衡因子为-2时，它的左子树平衡因子为1，这说明左子树的右子树高度是高于左子树的，这时需要以图中3节点，先进行左旋，最后在一5节点进行右旋。
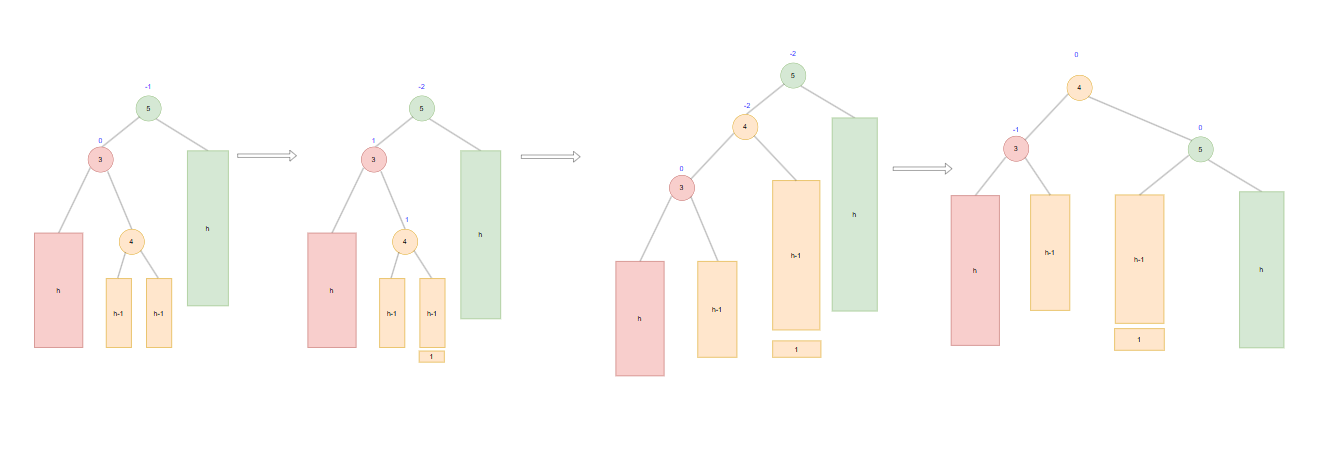
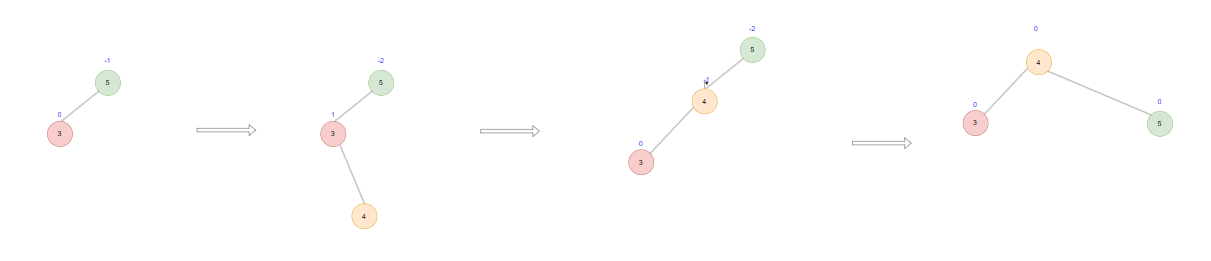
    在这里插入图片描述
    在这里插入图片描述

左右旋分为三种情况，1是给-2节点左子树的右子树的左子树高度加一。如第一个图上，导致4节点平衡因子为-1，这种，经过旋转后新的树的左子树平衡因子为0，右子树平衡因子为1，根的平衡因子为0.
2是给-2节点左子树的右子树的有子树高度加一。如第二个图上，导致4节点平衡因子为1，这种，经过旋转后新的树的左子树平衡因子为-1，右子树平衡因子为0，根的平衡因子为0.
3是图3这种情况，根的左子树的右子节点就是新插入的，此时4节点平衡因子为0。这种经过旋转后，根和左子树，右子树平衡因子都为0.

void RotateLR(node* root)
{
		int bf = root->_left->_right->_bf;//将-2节点左子树的右子树节点记下来
	node* SubL = root->_left;
	node* SubLR = root->_left->_right;//将平衡因子会改变的节点记下来。
	RotateL(SubL);
	RotateR(root);
	if (bf == 1)//
	{
		SubL->_bf = -1;
		SubLR->_bf = 0;
		root->_bf = 0;
	}
	else if (bf == -1)
	{
		SubL->_bf = 0;
		SubLR->_bf = 0;
		root->_bf = 1;
	}
	else if (bf == 0)
	{
		SubL->_bf = 0;
		SubLR->_bf = 0;
		root->_bf = 0;
	}
	else
	{
		assert("bf erron");
	}

}
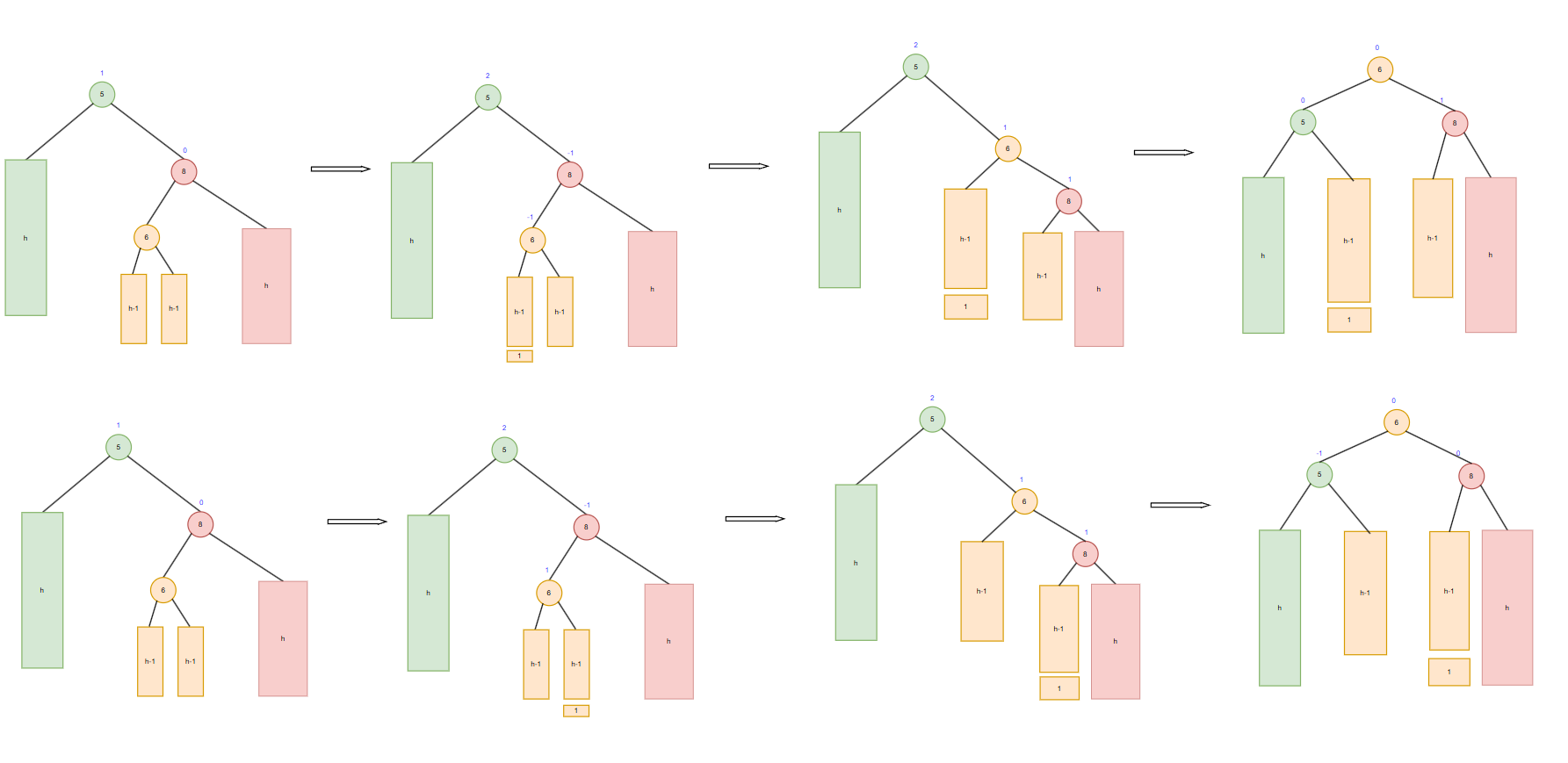
  1. AVL树的右左旋转

右左旋转是，根节点为2时，它的右子树平衡因子为-1时，进行的旋转。先对右子树进行右旋转，再对根进行左旋转。

右左旋转同样分为3种情况：

  1. 右子树的左子树平衡因子为1，旋转后右子树平衡因子为0，左子树平衡因子为-1，根平衡因子为0.
  2. 右子树的左子树平衡因子为-1，旋转后右子树平衡因子为1，左子树平衡因子为0，根平衡因子为0.
  3. 右子树的左子树平衡因子为0，旋转后右子树平衡因子为0，左子树平衡因子为0，根平衡因子为0.

在这里插入图片描述
在这里插入图片描述

void RotateRL(node* root)
{
	int bf = root->_right->_left->_bf;//将-2节点左子树的右子树节点记下来
	node* SubR = root->_right;
	node* SubRL = root->_right->_left;//将平衡因子会改变的节点记下来。
	RotateR(SubR);
	RotateL(root);
	if (bf == 1)//
	{
		SubR->_bf = 0;//旋转后原来的根右子节点成为了新树根的右子节点。
		SubRL->_bf = 0;//旋转后原来的根右子节点的左子节点成为了新的根。
		root->_bf = -1;//旋转后原来的根成为了新树根的左子节点。
	}
	else if (bf == -1)
	{
		SubR->_bf = 1;
		SubRL->_bf = 0;
		root->_bf = 0;
	}
	else if (bf == 0)
	{
		SubR->_bf = 0;
		SubRL->_bf = 0;
		root->_bf = 0;
	}
	else
	{
		assert("bf erron");
	}

}

总结：无论是左右双旋还是右左双旋，影响最后根，左子节点和右子节点平衡因子的因素是，高度改变的子树的平衡因子。若为-1，则旋转后的新树，左子节点平衡因子为0，右为1.若为1，则旋转后的新树，左子节点平衡因子为-1，右为0。若为0，则旋转后的新树，左右子节点平衡因子都为0.

  1. 二叉树高度和节点数量查询
{
	publi： 
	void Inoder()
	{
		_Inoder(_root);
	}
	int hight()
	{
		return _hight(_root);
	}
	int size()
	{

		return _size(_root);
	}
private:
	void _Inoder(node* root)
	{
		if (root == nullptr)
			return;
		_Inoder(root->_left);
		cout << "K: " << root->_kv.first << ";" << "V: " << root->_kv.second << ";" << "bf: " << root->_bf << endl;
		_Inoder(root->_right);
	}

	int _hight(node* root)
	{
		if (root == nullptr)
			return 0;


		return max(_hight(root->_left), _hight(root->_right)) + 1;
	}

	int _size(node* root)
	{
		if (root == nullptr)
			return 0;


		return _size(root->_left) + _size(root->_right) + 1;
	}
  1. 判断二叉树是否为AVL平衡
bool _isblance(node* root)
{
	if (root == nullptr)
		return true;

	int lefthight = _hight(root->_left);
	int righthight = _hight(root->_right);
	if (lefthight - righthight >= 2 || lefthight - righthight <= -2)
	{
		return false;
	}


	return _isblance(root->_left)&&_isblance(root->_right);
}

三. 整体代码

#pragma once
#include<iostream>
#include<vector>
#include<assert.h>
using namespace std;

template <class T ,class V>
struct AvlNode
{
	AvlNode<T,V>* _right;
	AvlNode<T,V>* _left;
	AvlNode<T,V>* _parent;
	std::pair<T, V> _kv;
	int _bf;

	AvlNode(const std::pair<T,V>& kv)
		:_right(nullptr)
		,_left(nullptr)
		,_parent(nullptr)
		,_kv(kv)
		,_bf(0)
		{

		}
	
};
template <class T, class V>
class AVLStree
{
	typedef AvlNode<T, V> node;

public:
	bool insert(const pair<T, V>& kv)
	{
		if (_root == nullptr)
		{
			_root = new node(kv);
			return true;
		}
		
		node* cur = _root;
		node* parent = nullptr;
		while (cur)
		{
			if (cur->_kv.first == kv.first)
			{
				return false;
			}
			else if (kv.first < cur->_kv.first)
			{
				parent = cur;
				cur = cur->_left;
			}
			else if (kv.first > cur->_kv.first)
			{
				parent = cur;
				cur = cur->_right;
			}
		}
		if (kv.first<parent->_kv.first)
		{
			parent->_left = new node(kv);
			cur = parent->_left;
			cur->_parent = parent;
			
		}
		else if (kv.first > parent->_kv.first)
		{	
			parent->_right = new node(kv);
			cur = parent->_right;
			cur->_parent = parent;
			
		}
		while (parent)
		{
			if (cur==parent->_right)
			{
				parent->_bf++;
			}
			else if (cur == parent->_left)
			{
				parent->_bf--;
			}

			if (parent->_bf == 0)
				break;
			else if (parent->_bf == 1 || parent->_bf == -1)
			{
				cur = parent;
				parent = parent->_parent;
			}
			else
			{
				if (parent->_bf == -2 && parent->_left->_bf==-1)//-2的左子节点，的左子树高度加1，右旋
				{
					RotateR(parent);
					return true;
				}
				else if (parent->_bf == 2 && parent->_right->_bf == 1)//-2的左子节点，的左子树高度加1，右旋
				{
					RotateL(parent);
					return true;
				}
				else if (parent->_bf == -2 && parent->_left->_bf == 1)
				{
					RotateLR(parent);
					return true;
				}
				else if (parent->_bf == 2 && parent->_right->_bf == -1)
				{
					RotateRL(parent);
					return true;
				}
			}

     		};



	}
	void RotateR(node* root)
	{
		node* cur = root->_left;//先拿到-2节点的左子节点
		root->_left = cur->_right;//根的左子树成为左子节点的右子树
		if(cur->_right)
		cur->_right->_parent = root;//左子节点的右子树的父亲改为根
		cur->_right = root;//让根成为左子树的右节点
		cur->_parent = root->_parent;//让左子树成为新的根节点
		if (root->_parent == nullptr)//判断该节点是否为_root
		{
			_root = cur;			//_root为原来的左子节点
			root->_parent = cur;
			root->_bf = 0;
			cur->_bf = 0;
			return;
			

		}
		else if (root->_parent->_left == root)
		{
			root->_parent->_left = cur;
		}
		else
		{
			root->_parent->_right = cur;
		}
		root->_parent = cur;//原来的根的父亲改为原来的左子节点
		root->_bf = 0;//将两个改变的平衡因子修改
		cur->_bf = 0;

	}

	void RotateL(node* root)
	{
		node* cur = root->_right;//先拿到-2节点的右子节点
		root->_right = cur->_left;//
		if (cur->_left)
			cur->_left->_parent = root;//右子节点的右子树的父亲改为根
		cur->_left = root;//让根成为右子树的左节点
		cur->_parent = root->_parent;//让右子树成为新的根节点
		if (root->_parent == nullptr)//判断该节点是否为_root
		{
			_root = cur;			//_root为原来的左子节点
			root->_parent = cur;
			root->_bf = 0;
			cur->_bf = 0;
			return;
		}
		else if (root->_parent->_left == root)
		{
			root->_parent->_left = cur;
		}
		else
		{
			root->_parent->_right = cur;
		}
		root->_parent = cur;//原来的根的父亲改为原来的右子节点
		root->_bf = 0;//将两个改变的平衡因子修改
		cur->_bf = 0;

	}
	void RotateLR(node* root)
	{
 		int bf = root->_left->_right->_bf;//将-2节点左子树的右子树节点记下来
		node* SubL = root->_left;
		node* SubLR = root->_left->_right;//将平衡因子会改变的节点记下来。
		RotateL(SubL);
		RotateR(root);
		if (bf == 1)//
		{
			SubL->_bf = -1;
			SubLR->_bf = 0;
			root->_bf = 0;
		}
		else if (bf == -1)
		{
			SubL->_bf = 0;
			SubLR->_bf = 0;
			root->_bf = 1;
		}
		else if (bf == 0)
		{
			SubL->_bf = 0;
			SubLR->_bf = 0;
			root->_bf = 0;
		}
		else
		{
			assert("bf erron");
		}

	}

	void RotateRL(node* root)
	{
		int bf = root->_right->_left->_bf;//将-2节点左子树的右子树节点记下来
		node* SubR = root->_right;
		node* SubRL = root->_right->_left;//将平衡因子会改变的节点记下来。
		RotateR(SubR);
		RotateL(root);
		if (bf == 1)//
		{
			SubR->_bf = 0;//旋转后原来的根右子节点成为了新树根的右子节点。
			SubRL->_bf = 0;//旋转后原来的根右子节点的左子节点成为了新的根。
			root->_bf = -1;//旋转后原来的根成为了新树根的左子节点。
		}
		else if (bf == -1)
		{
			SubR->_bf = 1;
			SubRL->_bf = 0;
			root->_bf = 0;
		}
		else if (bf == 0)
		{
			SubR->_bf = 0;
			SubRL->_bf = 0;
			root->_bf = 0;
		}
		else
		{
			assert("bf erron");
		}

	}
	void Inoder()
	{
		_Inoder(_root);
	}
	int hight()
	{
		return _hight(_root);
	}
	int size()
	{

		return _size(_root);
	}
	bool isblance()
	{
		
		return _isblance(_root);
	}
private:
	void _Inoder(node* root)
	{
		if (root == nullptr)
			return;
		_Inoder(root->_left);
		cout << "K: " << root->_kv.first << ";" << "V: " << root->_kv.second << ";" << "bf: " << root->_bf << endl;
		_Inoder(root->_right);
	}

	int _hight(node* root)
	{
		if (root == nullptr)
			return 0;


		return max(_hight(root->_left), _hight(root->_right)) + 1;
	}

	int _size(node* root)
	{
		if (root == nullptr)
			return 0;


		return _size(root->_left) + _size(root->_right) + 1;
	}

	bool _isblance(node* root)
	{
		if (root == nullptr)
			return true;

		int lefthight = _hight(root->_left);
		int righthight = _hight(root->_right);
		if (lefthight - righthight >= 2 || lefthight - righthight <= -2)
		{
			return false;
		}


		return _isblance(root->_left)&&_isblance(root->_right);
	}
private:

	node* _root = nullptr;
};
线索二叉树，搜索二叉树，AVL二叉树，满二叉树，完全二叉树，平衡二叉树，最优二叉树
ZJQ的博客
10-15 858
二叉树的遍历本质上是将一个复杂的非线性结构转换为线性结构，使每个结点都有了唯一前驱和后继（第一个结点无前驱，最后一个结点无后继）。对于二叉树的一个结点，查找其左右子女是方便的，其前驱后继只有在遍历中得到。为了容易找到前驱和后继，有两种方法。一是在结点结构中增加向前和向后的指针fwd和bkd，这种方法增加了存储开销，不可取；二是利用二叉树的空链指针。 二叉查找树（又：二叉搜索树，二叉排...
二叉树之AVL树
mrbone9的博客
03-09 840
今天来细说下 AVL 树，并结合图示代码来认识并掌握 AVL 树的创建，删除，体会下 AVL 特有的自平衡性。 本文涉及比较多的内容，鉴于时间关系，当你看到时可能是未完结章节，尽情期待 目录： AVL 概念 AVL 的旋转 AVL 树代码实现（C语言） 测试实例 AVL 概念 AVL 也是二叉树的一种，所以符合所有二叉树应有的特性，以及遍历方法 与二叉树不同的是，AVL树是一颗平衡树： 节点 root，左子节点的高度 与 右子节点的高度，最大差值 = 1 下面看看 AV
AVL(平衡二叉树)
qq_43701330的博客
07-26 555
AVL平衡树 最早的平衡二叉树之一。应用相对其他数据结构比较少。windows对进程地址空间的管理用到了AVL树。 定义 左右子树均为AVL树 左右子树的高度差的绝对值不超过1 平衡二叉树 满二叉树一定是平衡二叉树，高度最低 完全二叉树也是平衡二叉树，叶子节点深度相差不为1 线段树也是平衡二叉树，叶子节点深度相差不为1 下图中看起来比较偏斜，但是符合定义 平衡二叉树的高...
平衡二叉树AVL
冯Jungle的个人博客
07-12 430
对于有N个节点的二叉排序树，我们期望其高度是LogN，但实际情况往往事与愿违。在极端情况下，比如在生成二叉排序树时，其插入的序列是个有序数列，此时的二叉树结构类似于一个链表，各个操作的时间与链表的操作无异。因此，通过某种方法使得二叉树左右子树深度一样或者相差不大是有意义和必要的。这就是平衡二叉树，也叫AVL树。 1.AVL树定义 平衡二叉树要么是空树，要么满足以下性质 左右子树的高度之差的...
详解AVL树（平衡二叉树）
热门推荐
水澹澹兮生烟
09-20 2万+
插入节点后对树进行旋转调整，分为四种情况。 1.右单旋 当一个平衡二叉树满足具有较高左子树时（如下图A），且要插入的节点插入到了较高左子树的左侧，此时进行右单旋。
AVL二叉树的左旋和右旋保持平衡
wang20010104的博客
05-30 335
AVL二叉树的左旋和右旋保持平衡
数据结构-AVL树（图解+全面分析平衡二叉树）
2302_77620024的博客
04-09 4606
K _key;int _bf;,_key(key),_bf(0){}之所以使用三叉链结构，是因为AVL树的核心是通过平衡因子（BF）调整树的平衡性。当插入或删除节点时，需要沿着路径向上回溯到根节点，逐层更新祖先节点的平衡因子。通过_parent指针可以直接访问父节点，代码更简洁高效AVL树的旋转（左旋、右旋、双旋）需要调整父子节点的指向关系，涉及多个节点的指针修改。通过_parent指针，可以直接修改父节点对子节点的引用，无需从根节点重新定位父节点，减少指针操作的复杂度。
平衡搜索二叉树（AVL树）
m0_69323023的博客
01-09 2791
AVL树详解
AVL平衡二叉树
百味皆苦的博客
02-15 897
目录 什么是平衡二叉树，平衡因子  实现AVL树  基于AVL的映射map（接口在以前博客中） 基于AVL的集合set（接口在以前博客中）   什么是平衡二叉树，平衡因子          实现AVL树 package com.suanfa.AVLTree; import java.util.ArrayList; /** * AVL树，平衡二叉树，优化二分搜...
AVL平衡二叉树的插入与删除
Mr_1024的博客
12-07 391
什么是平衡二叉树 首先我们需要知道什么是平衡二叉树： 平衡二叉树又称为AVL树，它具有以下的性质： 1.它是一颗空树或它的左右两个子树的高度差绝对值不超过1； 2.左右子数都是一颗平衡二叉树； 我们今天的增加与删除是在二叉搜索树的情况下进行 那么什么是二叉搜索树呢？ 若二叉搜索树的左子树不空，则左子树上的所有节点的值均小于它的根节点的值； 若它的右子树不空，则右子树上所有节点的值均大于...
AVL树（平衡二叉搜索树）
2301_81265915的博客
08-16 3360
int _bf;, _bf(0), _kv(kv){}某节点的左子树与右子树的高度(深度)差即为该节点的平衡因子（BF,Balance Factor），平衡二叉树中不存在平衡因子大于 1或小于-1的节点。在一棵平衡二叉树中，节点的平衡因子只能取 0 、1 或者 -1 ，分别对应着左右子树等高，左子树比较高，右子树比较高。
AVL搜索二叉树C语言源代码
12-07
AVL搜索二叉树是一种自平衡的二叉搜索树，由G. M. Adelson-Velsky和E. M. Landis在1962年提出，因此得名AVL树。这种数据结构的主要特点是其左右子树的高度差不超过1，从而确保了搜索、插入和删除操作的高效性。下面...
AVL.rar_二叉树 控制台_基于avl
09-21
这个"AVL.rar_二叉树 控制台_基于avl"项目显然是一个用纯C语言编写的，用于在控制台环境下演示AVL树操作的程序，适用于Visual Studio 2008开发环境。 首先，我们要理解什么是AVL树。AVL树是由G. M. Adelson-Velsky...
C++模板实现的AVL二叉树统一在AVLTree.h文件中
资源摘要信息: "AVL树...因此，在某些情况下，如果数据的插入和删除操作非常频繁，而查询操作不那么频繁，可能会考虑使用其他类型的平衡二叉树，如红黑树，其调整平衡的操作比AVL树来得少，可能会有更高的整体性能。
C++在高性能互联网服务开发与系统优化中的应用与实战经验解析
2501_94180432的博客
11-23 860
虽然 Go、Python 等语言因开发效率而广受欢迎，但在需要极致性能、内存控制和高并发处理的场景中，C++ 的优势不可替代。：C++ 适合实现高并发的消息网关、缓存服务和负载均衡模块，通过 epoll、libevent 等技术实现事件驱动模型，提高处理效率。：在云原生架构下，C++ 负责关键性能模块，如实时数据处理、流量调度或算法计算，而高层业务逻辑可结合其他语言实现，形成多语言混合架构。：在实时数据处理、推荐系统或搜索引擎中，C++ 的高效计算能力和模板库支持，可显著提高数据处理速度和算法执行效率。
中国计算机学会（CCF）推荐学术会议-A（人工智能）：ACL 2026
iaast的博客
11-24 569
大会官网：https://2026.aclweb.org/录用率：20.3%（1699/8360，2025年）时间地点：2026年7月2日-加州·美国。截稿时间：2026年1月5日。CCF推荐：A（人工智能）
SystemC：sc_spawn
数字IC那些事儿的博客
11-24 88
下面给你 最清晰、最系统 的 讲解，包含概念、用法、典型例子、同步方式以及为什么它比 SC_THREAD 更强。 是 SystemC 动态创建进程（process）的机制，可在 运行时 创建线程或方法进程。普通 SystemC 写法：是 静态创建进程（在 elaboration 阶段创建）。但 可以在程序运行中创建进程：这是 动态进程（dynamic process）。类似于操作系统的： 动态创建线程Verilog 的 对应线程函数：函数：可以：你可以指定：它是 METHOD 还是 THREAD初始敏感
C 风格时间获取方式详解
LXdian_LX的博客
11-24 249
简单直接，性能较好广泛兼容各种 C/C++ 编译器不需要复杂的 C++ 标准库支持不是标准 C++ 函数（是 POSIX 标准）缓冲区大小需要手动管理时区处理相对基础对于跨平台代码，使用条件编译处理考虑使用strftime进行更安全的格式化在新项目中可以考虑使用 C++11 的<chrono>库嵌入式系统或资源受限环境需要与 C 代码交互的项目简单的日志记录和时间戳功能对性能要求较高的场景这种方法虽然"传统"，但在很多场景下仍然非常实用和高效。
C语言内存学习
最新发布
ysazt的博客
11-24 589
c语言中变量得内存存放及生命周期
C语言实现基于AVL二叉树的优先队列算法
资源摘要信息:"AVL树是一种自平衡二叉搜索树，由Adelson-Velsky和Landis于1962年提出，故称AVL树。在AVL树中任何节点的两个子树的高度最大差别为1，这使得AVL树在增加和删除节点时，通过旋转操作来维持这种平衡，...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

aaa最北边

你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值