LOF算法和NOF算法

LOF（局部离群因子，Local Outlier Factor）算法

原理是基于密度的异常检测方法，其核心思想是通过比较数据点与其邻域的密度差异来识别异常点。以下是LOF算法原理的详细阐述：

---

1. 局部性与密度差异

LOF算法的核心在于“局部性”和“密度差异”。它认为，如果一个点的局部密度显著低于其邻域点的密度，那么这个点很可能是异常点。这种局部性使得LOF能够有效处理数据集中不同密度区域的异常检测问题，而不会被全局密度所误导。

---

2. 关键概念

为了实现上述思想，LOF算法引入了几个关键概念：

(1) k距离（k-distance）

对于数据点 p ，其 k距离 是指点 p 到其第 k 个最近邻的距离。这里 k 是一个用户定义的参数，通常选择较小的整数（如10或20）。

(2) k距离邻域（k-distance neighborhood）

点 p 的 k距离邻域 是指包含 p 以及所有距离小于或等于 k 距离的点的集合。这个集合通常包含 k 个或更多点。

(3) 可达距离（Reachability Distance）

可达距离是LOF算法中一个重要的概念。对于点 p 和点 o ，从 p 到 o 的 可达距离 定义为：

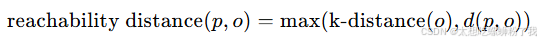
其中 d(p, o) 是点 p 和点 o 之间的实际欧氏距离。

解释：可达距离的目的是避免由于某个点 o 接近其他点而低估其邻域的密度。通过取 k 距离和实际距离的最大值，可以更公平地衡量点 o 的邻域密度。

(4) 局部可达密度（Local Reachability Density, LRD）

局部可达密度是衡量点 p 的邻域密度的指标。它定义为点 p 的 k 距离邻域内所有点的可达距离的倒数平均值：

解释：局部可达密度越高，说明点 p 的邻域越密集；反之，密度越低。

(5) 局部离群因子（LOF值）

局部离群因子（LOF值）是衡量点 p 是否为异常点的关键指标。它定义为点 p 的局部可达密度与其 k 距离邻域内所有点的局部可达密度的比值的平均值：

解释：

• 如果 LOF(p)≈1，说明点 p 的密度与邻域点的密度相近，不是异常点。
• 如果 LOF(p)>>1，说明点 ( p ) 的密度远低于其邻域点的密度，很可能是异常点。
• 如果 LOF(p)<1，说明点 ( p ) 的密度高于其邻域点的密度，但这种情况较少见。

---

3. 原理总结

LOF算法通过以下步骤实现异常检测：

1. 计算每个点的 k 距离和 k 距离邻域：确定每个点的局部邻域。
2. 计算可达距离：避免由于某个点过于接近其他点而低估其邻域密度。
3. 计算局部可达密度（LRD）：衡量每个点的邻域密度。
4. 计算LOF值：通过比较点的密度与其邻域点的密度，判断该点是否为异常点。

LOF值越高，说明点的局部密度与邻域密度的差异越大，越可能是异常点。

---

4. LOF原理的优势

• 局部性：LOF关注局部密度差异，能够有效处理数据集中不同密度区域的异常点。
• 无监督：不需要预先标注的正常或异常数据，适用于无标签数据集。
• 可解释性：通过LOF值可以直观地解释每个点的异常程度。

---

5. LOF原理的局限性

• 计算复杂度高：需要计算每个点的邻域和可达距离，时间复杂度较高，尤其在大规模数据集上效率较低。
• 参数选择敏感：( k ) 值的选择对结果影响较大，需要根据数据集进行调整。
• 对高维数据的适应性较差：在高维空间中，距离度量的效果会下降，可能导致性能下降。

---

6. 总结

LOF算法的原理基于密度的局部差异，通过计算可达距离、局部可达密度和LOF值，能够有效识别数据中的异常点。它特别适合于处理局部异常检测问题，但在大规模数据集或高维数据中可能需要进一步优化或调整参数。

---

源自kimi

---

NOF（自然离群因子 Natural Outlier Factor）算法

LOF算法引入自然邻域概念，自适应地获取邻域参数k。
NOF的优点在于去掉的邻域参数k，可以同时检测局部离群点和离群点簇。
自然离群因子（NOF值）

其中NIS为