全排列（递归做法）

排列：从n个元素中任取m个元素，并按照一定的顺序进行排列，称为排列；

全排列：当n==m时，称为全排列；

比如：集合{ 1,2,3}的全排列为：

{ 1 2 3}  { 1 3 2 }  { 2 1 3 }  { 2 3 1 }  { 3 2 1 }  { 3 1 2 }

排序思路：（递归）

 (1)n个元素的全排列=（n-1个元素的全排列）+（另一个元素作为前缀）；

(2)出口：如果只有一个元素的全排列，则说明已经排完，则输出数组；

(3)不断将每个元素放作第一个元素，然后将这个元素作为前缀，并将其余元素继续全排列，等到出口，出口出去后还需要还原数组；

用图形表示为：

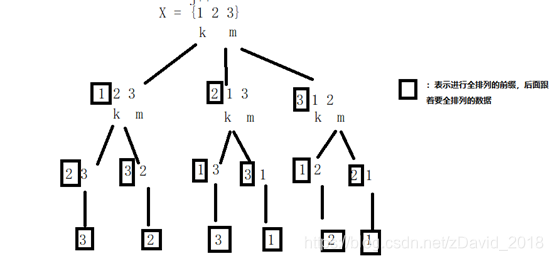
 黑色方框表示：选取每一个元素作为前缀，后面的数据再进行全排列，直到待排序队列只有一个元素，这时这一趟排列结束，打印出。

伪代码分析：

函数：Void Perm(int *arr,int head,int tail);

//参数说明：arr 数组地址，

//head:进行排列的第一个元素下标

//tail:进行排列最后一个元素下标

 

因为Perm(n) = arr[0]Perm（n-1）+arr[1] Perm（n-1）+……+arr[n-1] Perm（n-1）

所以这里用递归的做法，递归结束条件是Perm(1) = arr[x];

伪代码说明：

void Perm(int *arr,int head,int tail)
{
	if(head == tail)//如果相等 说明遍历到最后，没有元素能当前缀，所以这一趟全排列结束
	{
		ShowArray();//打印这一次排列的结果
	}
	else
	{
		For(int j = head ; j <= tail;j++)//j表示的每一个元素一次做前缀
		{
			Swap（arr[head],j）; //交换j到最前面 
			Perm(arr,head+1,tail); //全排列后面的所有元素（这里是head+1，而不是head++）
			Swap（arr[head],j）; //还需要将之前交换的再换回 否则整个数组顺序全被打乱
		}
	}
}
////全排列后面的所有元素（这里是head+1，而不是head++，head++代表参数++，递归的下一个head和上一个head不相同，所以要head+1计算）

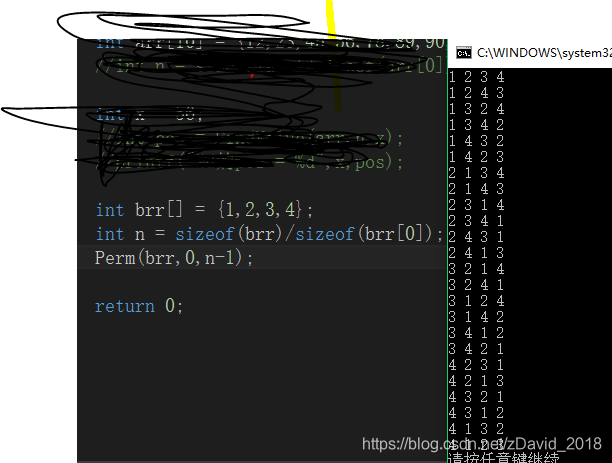
完整代码以及程序运行结果：

void ShowArray(int *arr,int len)
{
	for(int i = 0;i<len;i++)
	{
		cout<<arr[i]<<" ";
	}
	cout<<endl;
}
void Swap(int &a,int &b)
{
	int c= b;
	b= a;
	a = c;
}
void Perm(int *arr,int k,int m)
{
	if(k == m)//打印
	{
		ShowArray(arr,m+1);
	}
	else
	{
		for(int j = k;j<= m;j++)
		{
			Swap(arr[j],arr[k]);//j k 交换
			Perm(arr,k+1,m);
			Swap(arr[j],arr[k]);
		}
	}
}

 4个元素的全排列：