二叉树相关练习--2

目录

1、二叉树的层次遍历

2、判断是不是完全二叉树 

3、两个结点的最近公共祖先

4、根据前序与中序构造二叉树

5、根据后序与中序构造二叉树 

6、根据二叉树创建字符串

7、二叉树前序非递归遍历实现

8、二叉树中序非递归遍历实现 

9、二叉树后序非递归遍历实现

---

1、二叉树的层次遍历

oj：102. 二叉树的层序遍历 - 力扣（LeetCode）

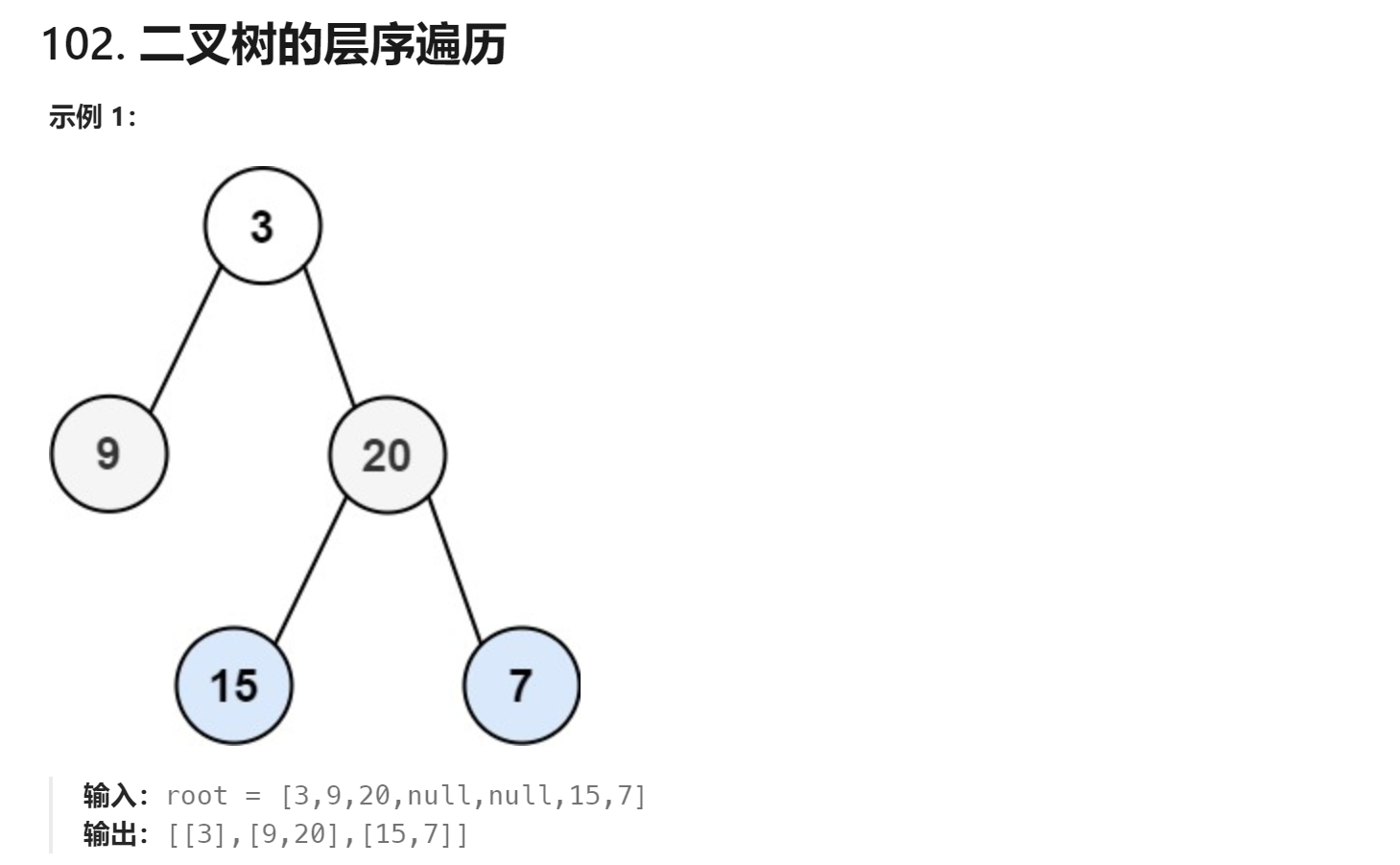
    // 标准层次遍历
    void levelOrder(TreeNode root) {
        if(root == null) {
            return;
        }
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        while (!queue.isEmpty()) {
            TreeNode cur = queue.poll();
            System.out.print(cur.val+" ");

            if(cur.left != null) {
                queue.offer(cur.left);
            }
            if(cur.right != null) {
                queue.offer(cur.right);
            }
        }
    }

    // 符合力扣题目的层次遍历
    public List<List<Integer>> levelOrder2(TreeNode root) {
        List<List<Integer>> ret = new ArrayList<>();
        if(root == null) {
            return ret;
        }
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);//A

        while (!queue.isEmpty()) {
            int size = queue.size();//1
            List<Integer> tmp = new ArrayList<>();
            while (size != 0) {
                TreeNode cur = queue.poll();
                //System.out.print(cur.val + " ");
                tmp.add(cur.val);
                size--;//0
                if (cur.left != null) {
                    queue.offer(cur.left);
                }
                if (cur.right != null) {
                    queue.offer(cur.right);
                }
            }
            ret.add(tmp);
        }
        return ret;
    }

2、判断是不是完全二叉树 

思路：

1. 与层次遍历不同的是，结点的左右子树为null，null也有入队

2. 出队时若遇到null，则跳出循环

3. 再判断队列中是否还有不为空的元素，有则不是完全二叉树，全为空则是

注：队列中的元素全为空，队列不为空，有几个元素 大小就是几

    // 判断一棵树是不是完全二叉树
    boolean isCompleteTree(TreeNode root) {
        if(root == null) {
            return true;
        }
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);

        while (!queue.isEmpty()) {
            TreeNode cur = queue.poll();
            if(cur != null) {
                queue.offer(cur.left);
                queue.offer(cur.right);
            }else {
                break;//结束这个循环
            }
        }
        //需要判断队列当中 是否有非空的元素
        while (!queue.isEmpty()) {
            //一个元素 一个元素 出队来判断 是不是空
            TreeNode tmp = queue.peek();
            if(tmp == null) {
                queue.poll();
            }else {
                return false;
            }
        }
        return true;
    }

3、两个结点的最近公共祖先

oj：236. 二叉树的最近公共祖先 - 力扣（LeetCode）

思路：

1. 如果root是p或q中的一个，那么root就是最近公共祖先

2. 如果p和q分布在root的左右两侧，那么root就是最近公共祖先

3. p和q在root的同一侧，递归左右子树，遇到p或q就返回，左边为空右边不为空，最近公共祖先就是右边这个不为空的值，反之亦然

4. p和q在root的同一侧，在下图的这种情况，返回的右边不为空的值是root

    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if(root == null) return null;
        if(root == p || root == q) {
            return root;
        }
        TreeNode leftTree = lowestCommonAncestor(root.left,p,q);
        TreeNode rightTree = lowestCommonAncestor(root.right,p,q);
        if(leftTree != null && rightTree != null) {
            return root;
        }else if(leftTree != null) {
            return leftTree;
        }else {
            return rightTree;
        }
    }

思路2：

1. 把根节点到p和q路径上的所有节点使用栈保存下来

2. 比较两个栈的大小，大的出栈两个栈的差值次

3. 然后依次对两个栈的栈顶元素比较，不相同则一起出栈，相同则是公共祖先

    public TreeNode lowestCommonAncestor2(TreeNode root, TreeNode p, TreeNode q) {

        if(root == null) return null;

        Stack<TreeNode> stackP = new Stack<>();
        Stack<TreeNode> stackQ = new Stack<>();

        getPath(root,p,stackP);
        getPath(root,q,stackQ);

        int sizeP = stackP.size();
        int sizeQ = stackQ.size();

        if(sizeP > sizeQ) {
            int size = sizeP - sizeQ;
            while(size != 0) {
                stackP.pop();
                size--;
            }

        }else {
            int size = sizeQ - sizeP;
            while(size != 0) {
                stackQ.pop();
                size--;
            }
        }
        //两个栈当中的元素是一样多
        while(!stackP.isEmpty() && !stackQ.isEmpty()) {
            if(stackP.peek() == stackQ.peek()) {
                return stackP.peek();
            }else{
                stackP.pop();
                stackQ.pop();
            }
        }

        return null;
    }

    private boolean getPath(TreeNode root,TreeNode node,Stack<TreeNode> stack) {
        if(root == null || node == null) {
            return false;
        }
        stack.push(root);
        if(root == node) {
            return true;
        }
        boolean flg = getPath(root.left,node,stack);
        if(flg) {
            return true;
        }
        boolean flg2 = getPath(root.right,node,stack);
        if(flg2) {
            return true;
        }

        stack.pop();

        return false;
    }

4、根据前序与中序构造二叉树

oj：105. 从前序与中序遍历序列构造二叉树 - 力扣（LeetCode）

下方代码中成员变量 preIndex 之所以不用static修饰，是因为被static修饰的成员变量 只有一份，他是和很多对象共享的。如果题目只有一个测试用例可以用static修饰

class SolutionCreateTree {

    static class TreeNode {
        public int val;
        public TreeNode left;
        public TreeNode right;

        public TreeNode(int val) {
            this.val = val;
        }
    }

    public int preIndex ;
    public TreeNode buildTree(int[] preorder, int[] inorder) {

        return buildTreeChilde(preorder,inorder,0,inorder.length-1);

    }

    private TreeNode buildTreeChilde(int[] preorder,int[] inorder,int inbegin,int inend) {

        if(inbegin > inend) {
            return null;//没有 左树 或者 没有 右树 
        }

        TreeNode root = new TreeNode(preorder[preIndex]);

        int rootIndex = findIndexRoot(inorder,inbegin,inend,preorder[preIndex]);
        if(rootIndex == -1) {
            return null;
        }

        preIndex++;

        root.left = buildTreeChilde(preorder,inorder,inbegin,rootIndex-1);

        root.right = buildTreeChilde(preorder,inorder,rootIndex+1,inend);
        
        return root;

    }

    private int findIndexRoot(int[] inorder,int inbegin, int inend,int key) {

        for(int i = inbegin; i <= inend;i++) {
            if(inorder[i] == key) {
                return i;
            }
        }
        return -1;
    }
}

5、根据后序与中序构造二叉树 

oj：106. 从中序与后序遍历序列构造二叉树 - 力扣（LeetCode）

class SolutionCreateTree2 {
    public int postIndex;
    public TreeNode buildTree(int[] inorder, int[] postorder) {

        postIndex = postorder.length-1;
        return buildTreeChilde(postorder,inorder,0,inorder.length-1);
    }


    private TreeNode buildTreeChilde(int[] postorder,int[] inorder,int inbegin,int inend) {
        if(inbegin > inend) {
            return null;//没有 左树 或者 没有 右树 
        }
        TreeNode root = new TreeNode(postorder[postIndex]);

        int rootIndex = findIndexRoot(inorder,inbegin,inend,postorder[postIndex]);
        if(rootIndex == -1) {
            return null;
        }
        postIndex--;

        root.right = buildTreeChilde(postorder,inorder,rootIndex+1,inend);

        root.left = buildTreeChilde(postorder,inorder,inbegin,rootIndex-1);
        
        return root;
    }

    private int findIndexRoot(int[] inorder,int inbegin, int inend,int key) {

        for(int i = inbegin; i <= inend;i++) {
            if(inorder[i] == key) {
                return i;
            }
        }
        return -1;
    }
}

6、根据二叉树创建字符串

oj：606. 根据二叉树创建字符串 - 力扣（LeetCode）

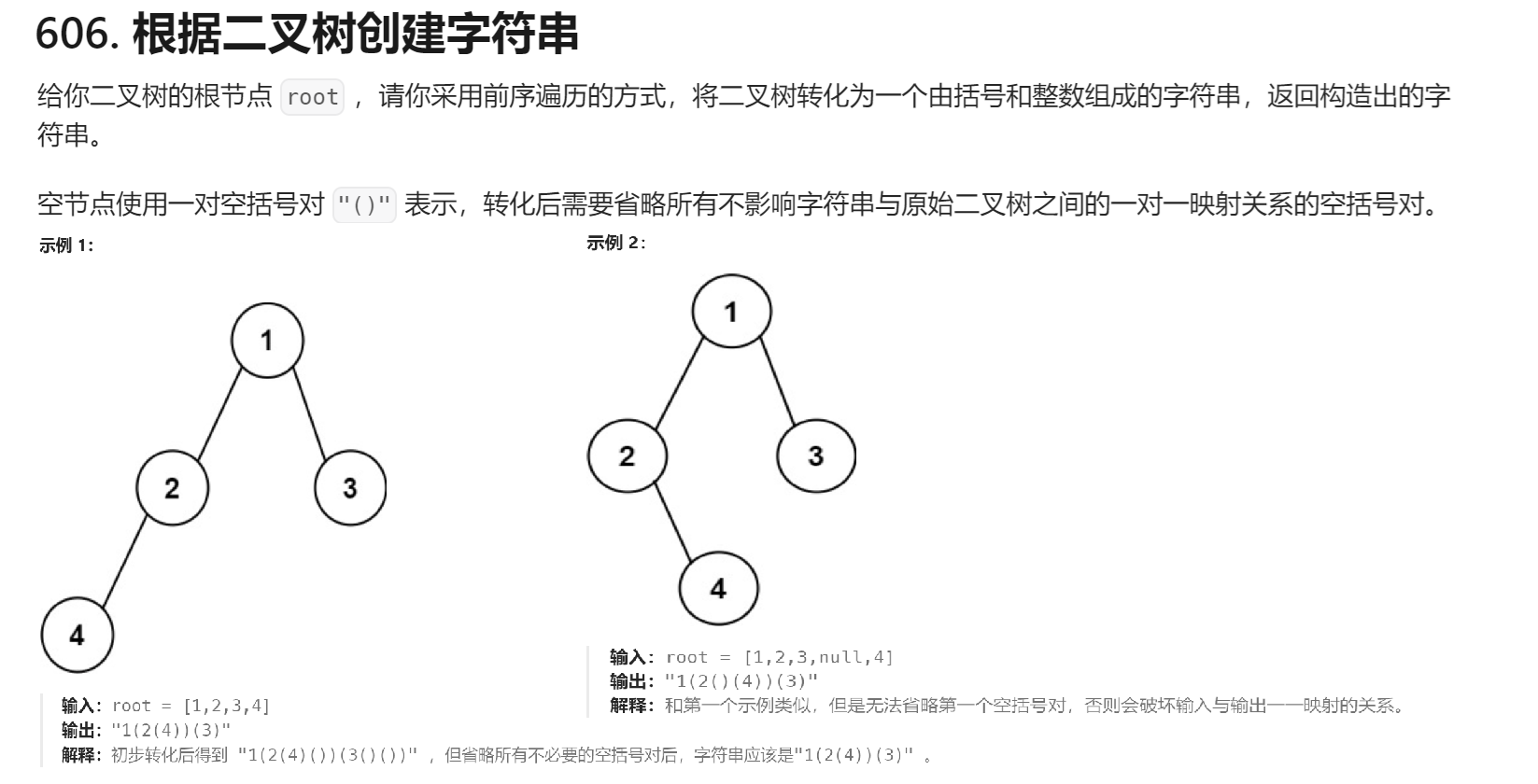
思路：

大方向：采用前序遍历的方式进行遍历

1. 根节点直接拼接

2. 左边为空&&右边为空的时候什么都不做

3. 左边不为空 右边为空，对左边递归

4. 左边为空 右边不为空，对左边加一对括号，对右边递归

    public String tree2str(TreeNode root) {
        StringBuilder stringBuilder = new StringBuilder();
        tree2strChild(root,stringBuilder);
        return stringBuilder.toString();
    }

    private void tree2strChild(TreeNode t,StringBuilder stringBuilder) {
        if(t == null) {
            return ;
        }
        stringBuilder.append(t.val);
        if(t.left != null) {
            stringBuilder.append("(");
            tree2strChild(t.left,stringBuilder);
            stringBuilder.append(")");
        }else {
            if(t.right == null) {
                return;
            }else {
                stringBuilder.append("()");
            }
        }
        //判断右树
        if(t.right != null) {
            stringBuilder.append("(");
            tree2strChild(t.right,stringBuilder);
            stringBuilder.append(")");
        }else {
            return;
        }
    }

7、二叉树前序非递归遍历实现

oj：144. 二叉树的前序遍历 - 力扣（LeetCode）

    void preOrderNor(TreeNode root){
        if(root == null) {
            return;
        }
        Stack<TreeNode> stack = new Stack<>();
        TreeNode cur = root;
        while (cur != null || !stack.isEmpty()) {
            while (cur != null) {
                stack.push(cur);
                System.out.print(cur.val + " ");
                cur = cur.left;
            }
            TreeNode top = stack.pop();
            cur = top.right;
        }
    }

8、二叉树中序非递归遍历实现 

oj：94. 二叉树的中序遍历 - 力扣（LeetCode）

1. 一直往左走遇到空停止，左树走完了弹出栈顶元素、并且打印

2. 遍历弹出节点的右子树

    void inOrderNor(TreeNode root){
        if(root == null) {
            return;
        }
        Stack<TreeNode> stack = new Stack<>();
        TreeNode cur = root;
        while (cur != null || !stack.isEmpty()) {
            while (cur != null) {
                stack.push(cur);
                cur = cur.left;
            }
            TreeNode top = stack.pop();
            System.out.print(top.val + " ");
            cur = top.right;
        }
    }

9、二叉树后序非递归遍历实现

oj：145. 二叉树的后序遍历 - 力扣（LeetCode）

    void postOrderNor(TreeNode root){
        if(root == null) {
            return;
        }
        Stack<TreeNode> stack = new Stack<>();
        TreeNode cur = root;

        // prev用于记录最新被打印的节点
        TreeNode prev = null;
        while (cur != null || !stack.isEmpty()) {
            while (cur != null) {
                stack.push(cur);
                cur = cur.left;
            }
            TreeNode top = stack.peek();

            if(top.right == null || top.right == prev) {
                System.out.print(top.val+" ");
                stack.pop();
                prev = top;
            }else {
                cur = top.right;
            }
        }
    }