红黑树与2-3树的等价性->深入理解红黑树

2-3树定义

• 节点可以存放一个或者两个元素,称为2节点和3节点(这也是2-3树名称的由来),如下图
  
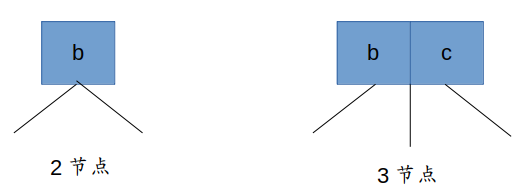
• 是一棵绝对平衡的二插树,下图示例就是一个2-3树
  • 任意一个节点到叶子节点的深度是一致的
• 满足二分搜索树的基本性质,即 中序遍历的结果是有序
  • 二节点 -> 左节点<中间节点<右节点,如图中的以52为根节点的子树
  • 三节点 -> 左节点<中左节点<中间节点<中右节点,小于右节点,如图中以19\32为根节点的子树
    

2-3树的绝对平衡性-添加节点

• 二节点中添加一个元素,形成一个新的三节点
  
• 三节点中添加一个元素(三节点为根节点)
  • 临时形成一个四节点
  • 再拆分成一棵由三个二节点组成的平衡的子树
    
• 三节点添加一个元素(三节点不为根节点,父节点为二节点)
  • 临时形成一个四节点
  • 再拆分成一个由三个二节点组成的子树
  • 子树的根向上融合成为3节点
    
• 三节点添加一个元素(三节点不为根节点,父节点为三节点)
  • 临时形成一个四节点
  • 再拆分成一个由三个二节点组成的子树
  • 子树的根节点像上融合成四节点
  • 父节点再拆分一个由三个二节点组成的子树
    
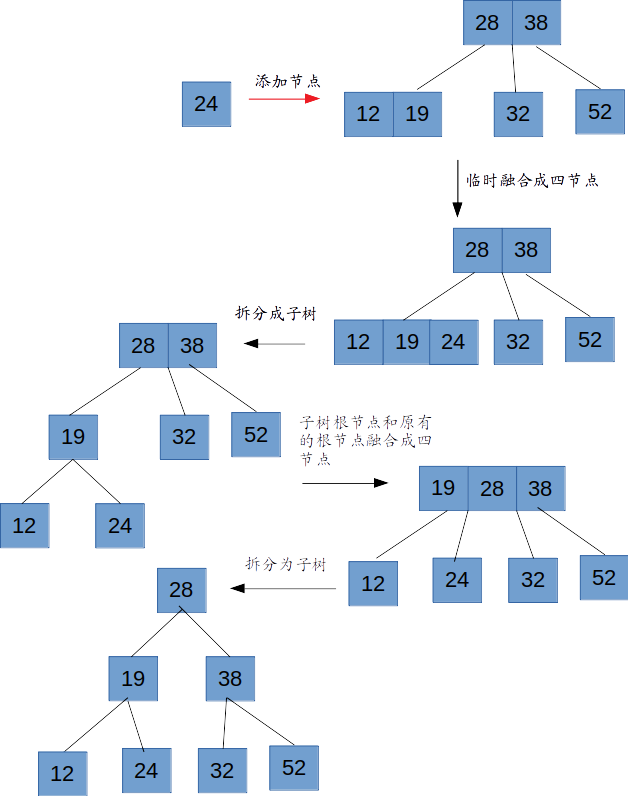
    综上,举了几种新增节点的栗子(没有列举到的,请自行类比),保证了2-3树的绝对平衡性,即根节点到叶子节点的深度都是一致的

红黑树与2-3树的等价性

2-3树中存在3节点,如果类比到二叉树,则需要引入一个同层的概念,在红黑树中,则以红色节点作为同层的存在,将红色节点置为左节点则称为左倾红黑树,以下所有的讨论都是基于左倾红黑树,如图

红黑树的性质

于此,我相信读者应该可以理解红黑树的基本性质了

• 每个节点或者是红色,或者是黑色
• 根节点是黑色的
• 每一个叶子节点(最后的空节点)是黑色的
  • 这条与其说是性质,不如说是定义,叶子节点=最后的空节点,并且叶子节点都是黑色的
• 如果一个节点是红色的,那么他的其他孩子节点都是黑色的
  • 红黑树本身就是2-3树在二叉树上的类比,假设有两个连续的红色节点,则类比成2-3树,如图所示(并不是一棵完整的红黑树),而2-3树本身仅支持2\3节点,所以该性质得证
    
  • 从任意一个节点到叶子节点,经过的黑色节点数是一样的.该性质其实就是2-3树的绝对平衡性,任意一个节点到叶子节点的深度是一致的,红色节点仅是引入的同层概念,所以该性质成立.也可以称红黑树是一棵黑平衡的树

红黑树添加新节点

基本原理

• 类比于向2-3树中添加一个新元素
• 永远添加红节点

举例说明

• 插入根节点
  • 新节点放置在根节点的位置
  • 将根节点置为黑色
    
• 插入非根节点,图图所示,共有3种情况
  

1. 新节点放置在父节点的右节点,则经过一次颜色翻转(如下图)即可
   

伪代码如下

node.color = RED;
node.left.color = BLACK;
node.right.color = BLACK;

2. 新节点放置在红色节点的左节点

• 对父节点进行右旋转(如图,其中:node为根节点,x为红节点,N为新节点,T1为node的右节点,T2为x的右节点)
  1. 断开x和node,将T2置为node的左节点
  2. 将node置为x的右节点
  3. x置为node的颜色,node的颜色置为红
     

伪代码如下

node.left = T1;
x.right = node;
x.color = node.color;
node.color = RED;

• 再进行颜色翻转

3. 新节点放置在红色节点的右节点

• 红节点进行左旋转(如图,x为红节点,N为新节点,T1为x的左节点,T2为N的左节点,T3为N的右节点,此处设置了T2\T3是为了保证一般性,事实上,在新增节点时,T2\T3均为空)
  1. 断开x和N,T2置为x的右节点
  2. x置为N的左节点
     

伪代码如下

x.right = N.left;
N.left = x;

• 黑节点进行右旋转
• 最后进行颜色翻转

红黑树优化拓展

以上笔者所有的讨论都是基于左倾红黑树,为了保证左倾的性质,做了一些额外的处理(删除节点时会有区别,笔者本文中没有讨论),而在红黑树的定义中并没有规定要左倾,即以下两种形式的节点,依旧是满足红黑树性质的

除了以上5条性质外,更优化的红黑树还包含了另一条性质

• 任何不平衡都会在三次旋转内解决(新增节点->2次旋转,删除节点->3次旋转)