（四）搜索

DFS（深度优先搜索）

DFS的框架

 DFS模板题：搜索和输出所有路径

 

 第44行使用了 “输出最短路径的简单方法”，path[][]记录路径，path[x][y]记录了从起点到点(x,y)的完整路径。这种方法浪费空间，适用于小图。

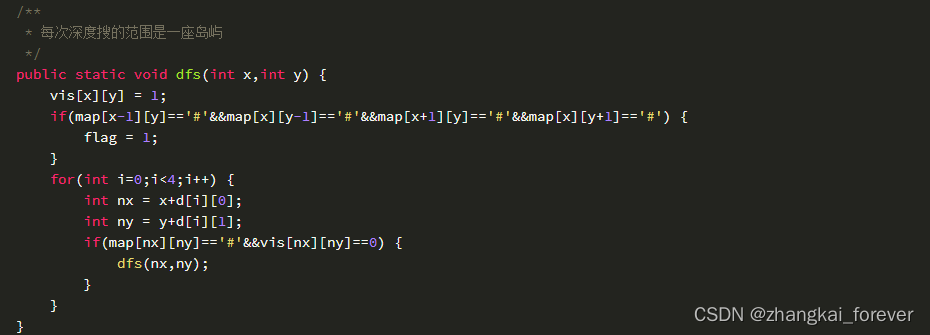
例题：全球变暖（DFS实现）

 DFS连通性判断：图论的一个简单问题，给定一张图，图由点和连接点的边组成，找到图中互相连通的部分。

连通性问题，计算步骤：

 

 

剪枝是指把不会产生答案的，不必要的枝条剪掉，是搜索常用的优化手段，降低计算量和复杂度

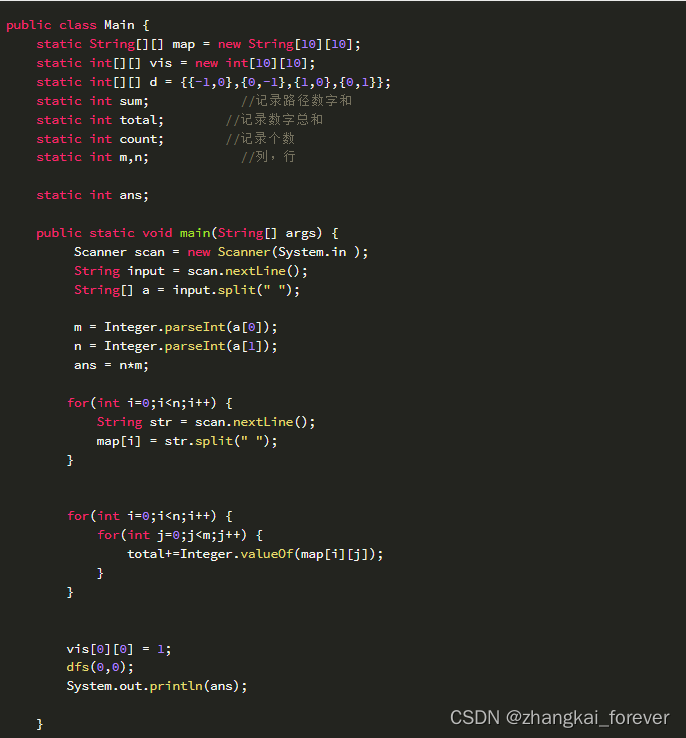
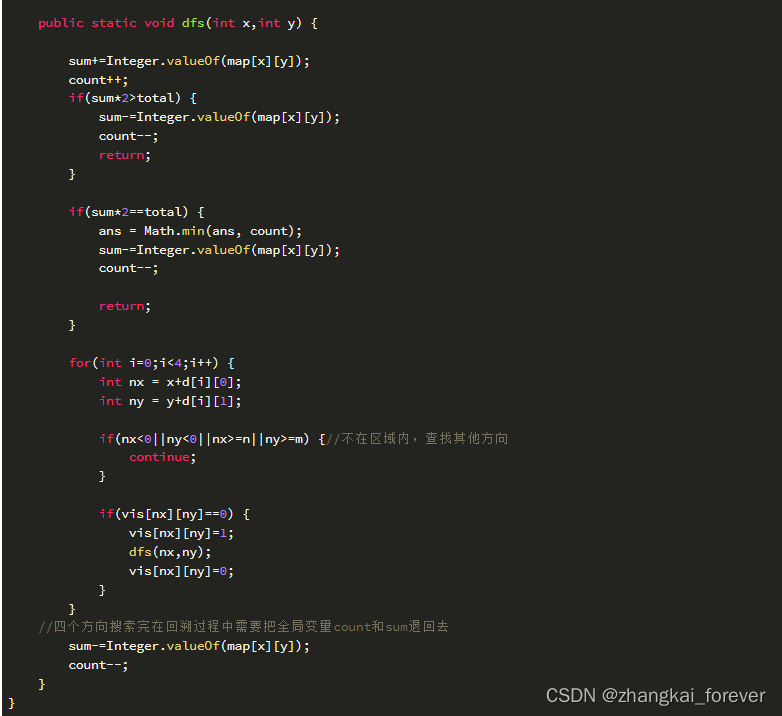
剪格子

 思路：先计算所有格子的和sum，再找一个连通区域，看区域的和是否为sum/2。

 剪枝：如果连通区域的和超过sum/2，就不需要再dfs了。

 

 

 路径问题：DFS和BFS

BFS（广度优先搜索）

应用：一般用于求最短路径问题，点和点的直接距离是1，即边长是1

用队列实现，从起点出发，按层次从近到远，逐层先后搜索，先搜到的层离起点更近。

 

 

 迷宫

 

输出路径：简单方法、标准方法

 

搜索范围较大时，用标准方法

 

 

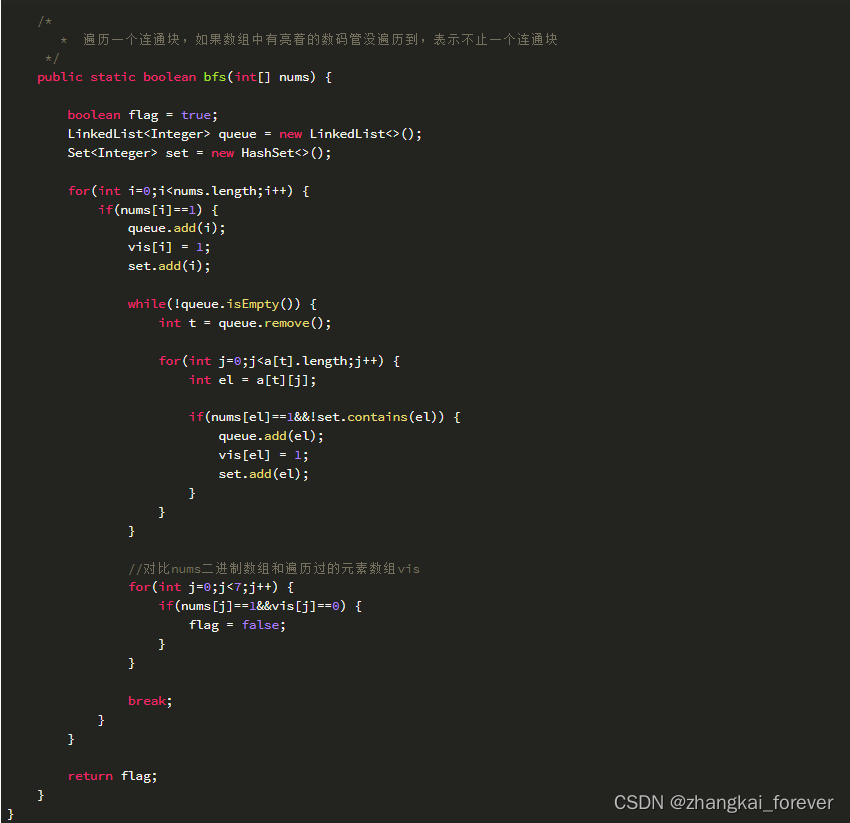
 BFS:连通性判断

 以全球变暖为例

 

练习：

跳蚱蜢

如果用DFS搜索，路径太多，

求最少跳跃，也是最短路径问题，这是一道典型的 BFS 题。

直接让蚱蜢跳到空盘有点麻烦，因为有很多蚱蜢在跳，跳晕了。如果反过来看，让空盘跳，跳到蚱蜢的位置，就简单多了，只有一个空盘在跳。

题目给的是一个圆，不好处理，用一个建模技巧“化圆为线”，把圆形转换为线形。把空盘看成 0，那么一个圆圈上有 9 个数字 {0,1,2,3,4,5,6,7,8}，拉直成了一条线上的 9 个数字，这条线的首尾两个数字处理成相连的。

这一题是八数码问题，八数码是经典的 BFS 问题。八数码问题有 9 个数字{0, 1, 2, 3, 4, 5, 6, 7, 8}，共有 9！= 362880 种排列，不算多。

此时初始状态是“012345678”，目标状态是“087654321”。

从初始状态“012345678”跳一次，有 4 种情况：

“102345678”、 “210345678”、 “812345670”、 “712345608”。

然后从这 4 种状态继续跳到下一种状态，一直跳到目标状态为止。

用BFS逐层搜索，当队列弹出终点“087654321”时，此时的深度就是跳跃的最小次数。

这里我们需要封装一个Node类，记录跳跃的深度和当前状态，

另外，如果不去重需要跳4^20次，因此需要做去重，如果跳到曾经出现过的状态，就不再继续搜索，一共有9!种状态。利用hashset对重复的跳跃做去重，代码如下

 七段码

本题最快的办法是手动数，比编码快一些。