给出两个字符串text和pattern,其中pattern为text的子串,求出pattern在text中所有出现的位置。
为了减少骗分的情况,接下来还要输出子串的前缀数组next。
输入格式:
第一行为一个字符串,即为text。
第二行为一个字符串,即为pattern。
输出格式:
若干行,每行包含一个整数,表示pattern在text中出现的位置。
接下来1行,包括length(pattern)个整数,表示前缀数组next[i]的值,数据间以一个空格分隔,行尾无多余空格。
输入样例:
ABABABC
ABA
输出样例:
1
3
0 0 1
样例说明:
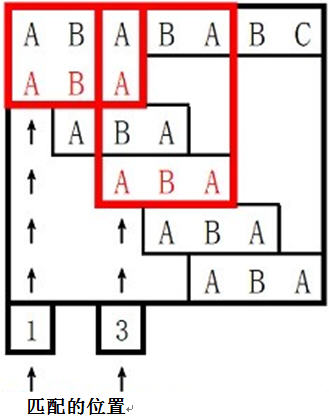
/*
#include<stdio.h>
#define MaxSize 500000
int nextval[MaxSize];
void GetNextval(char p[], int lp)
{
int j = 0, k = -1;
nextval[0] = -1;
while (j < lp)
{
if (k == -1 || p[j] == p[k])
{
j++;
k++;
nextval[j] = k;
}
else
k = nextval[k];
}
}
void KMPIndexl(char t[], char p[], int lt, int lp)
{
int i = 0, j = 0;
while (i < lt)
{
if (j == -1 || t[i] == p[j])
{
i++;
j++;
}
else
j = nextval[j];
if (j == lp)
{
printf(" %d\n", i - j+1);
j=nextval[j];
}
}
}
int main()
{
char t[MaxSize], p[MaxSize];
int lt = 0, lp = 0;
while ((t[lt] = getchar()) != '\n')
lt++;
while ((p[lp] = getchar()) != '\n')
lp++;
GetNextval(p, lp);
KMPIndexl(t, p, lt, lp);
for(int i=1;i<lp;i++)
printf("%d ",nextval[i]);
printf("%d\n",nextval[lp]);
return 0;
}
*/
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
char s[1000001],t[100001];
int next[1000001];
int lens,lent;
void GetNext()
{
int i=0,j=-1;
next[i]=j;
while(i<lent)
{
if(j==-1||t[j]==t[i])
{
i++;
j++;
next[i]=j;
}
else
j=next[j];
}
}
int KMP()
{
int i=0,j=0;
while(i<lens)
{
if(j==-1||s[i]==t[j])
{
i++;
j++;
}
else
{
j=next[j];
}
if(j==lent)
{
printf("%d\n",i-j+1);
j=next[j];
}
}
}
int main()
{
int i;
gets(s);
gets(t);
lens=strlen(s);
lent=strlen(t);
GetNext();
KMP();
for(i=1;i<lent;i++)
printf("%d ",next[i]);
printf("%d\n",next[lent]);
return 0;
}




 博客围绕给定两个字符串text和pattern,求pattern在text中所有出现位置及子串的前缀数组next展开。介绍了输入输出格式、样例,还给出了使用KMP算法实现该功能的C语言代码。
博客围绕给定两个字符串text和pattern,求pattern在text中所有出现位置及子串的前缀数组next展开。介绍了输入输出格式、样例,还给出了使用KMP算法实现该功能的C语言代码。
















 2269
2269

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








