java实现二叉树创建删除以及递归非递归遍历demo示例

基本概念

二叉树：每个节点最多有两颗子树，即左子树和右子树，次序不可以颠倒（即先有左才能有右）

满二叉树：除最后一层无任何子节点外，每一层上的所有节点都有两个子节点二叉树。即如果一个二叉树的层数为k，且节点总数是2^k-1，则它就是满二叉树。

平衡二叉树：它是一颗空树或者它的左右两个子树的高度差的绝对值不能超过1，并且左右两个子树都是一颗平衡二叉树。平衡二叉树的常用实现方法有红黑树（非严格平衡的二叉查找树）、AVL（平衡二叉搜索树）、替罪羊树、Treap、伸展树等。

二叉树高度：顾名思义就是二叉树的层数

广度优先遍历：即是层次遍历，从上往下对每一层依次访问，在每一层中，从左往右（也可以从右往左）访问结点，访问完一层就进入下一层，直到没有结点可以访问为止。

深度优先遍历：对每一个可能的分支路径深入到不能再深入为止，而且每个结点只能访问一次。要特别注意的是，二叉树的深度优先遍历比较特殊，可以细分为前（先）序遍历、中序遍历、后序遍历。前中后序遍历主要针对的是根节点访问的具体时机，具体说明如下：

1）前（先）序遍历：对任一子树，先访问根，然后遍历其左子树，最后遍历其右子树，即 中->左->右

2）中序遍历：对任一子树，先遍历其左子树，然后访问根，最后遍历其右子树，即 左->中->右

3）后序遍历：对任一子树，先遍历其左子树，然后遍历其右子树，最后访问根，即 左->右->中

二叉树的深度优先遍历的非递归的通用做法是采用栈（先进后出），而广度优先遍历的非递归的通用做法是采用队列（先进先出）

二叉树操作

二叉树对象

/**
 * 二叉树
 **/
public class BinaryTree<T extends Comparable<T>> {
    //根节点
    private Node root;

    class Node {
        //节点数据
        private T data;
        //父节点
        private Node parent;
        //左子节点
        private Node leftChild;
        //右子节点
        private Node rightChild;

        // 构造方法
        public Node(T data) {
            this.data = data;
        }
    }

    public Node root() {
        return root;
    }

}

二叉树创建、删除

 /**
     * 增加节点
     *
     * @param data
     * @return
     */
    public boolean add(T data) {
        boolean flag = false;
        if (!exist(data)) {
            Node newNode = new Node(data);
            if (root == null) {
                root = newNode;
            } else {
                // 找到父节点
                Node parent = findParent(data);
                if (parent != null) {
                    if (parent.data.compareTo(data) > 0) {
                        parent.leftChild = newNode;
                    } else {
                        parent.rightChild = newNode;
                    }
                    //新建节点的parent指向父节点
                    newNode.parent = parent;
                }
            }
            flag = true;
        }
        return flag;
    }

    /**
     * 删除节点
     *
     * @param data
     * @return
     */
    public boolean remove(T data) {
        boolean flag = false;
        Node node = getNode(data);
        if (node != null) {
            if (node == root) {
                // 删除的是根节点
                if (node.leftChild == null && node.rightChild == null) {
                    root = null;
                } else if (node.leftChild != null && node.rightChild == null) {
                    node.leftChild.parent = null;
                    root = node.leftChild;
                } else if (node.leftChild == null && node.rightChild != null) {
                    node.rightChild.parent = null;
                    root = node.rightChild;
                } else {
                    //找到要删节点的左节点
                    Node leftChild = split(data);
                    root = leftChild;
                    leftChild.parent = null;
                }
            } else {
                // 删除的是根节点
                if (node.leftChild == null && node.rightChild == null) {
                    if (node.data.compareTo(node.parent.data) < 0) {
                        node.parent.leftChild = null;
                    } else {
                        node.parent.rightChild = null;
                    }
                } else if (node.leftChild != null && node.rightChild == null) {
                    node.leftChild.parent = node.parent;
                    node.parent.rightChild = node.leftChild;
                } else if (node.leftChild == null && node.rightChild != null) {
                    node.rightChild.parent = node.parent;
                    node.parent.rightChild = node.rightChild;
                } else {
                    //找到要删节点的左节点
                    Node leftChild = split(data);
                    node.parent.leftChild = node.leftChild;
                    leftChild.parent = node.parent;
                }
            }
            flag = true;
        }
        return flag;
    }

    /**
     * 节点是否存在
     *
     * @param data
     * @return
     */
    public boolean exist(T data) {
        boolean flag = false;
        //从根节点开始遍历
        Node temp = root;
        while (temp != null) {
            if (temp.data.compareTo(data) == 0) {
                flag = true;
            } else if (temp.data.compareTo(data) > 0) {
                temp = temp.leftChild;
            } else {
                temp = temp.rightChild;
            }
        }
        return flag;
    }

    /**
     * 获取节点
     *
     * @param data
     * @return
     */
    public Node getNode(T data) {
        //从根节点开始遍历
        Node temp = root;
        while (temp != null) {
            if (temp.data.compareTo(data) == 0) {
                return temp;
            } else if (temp.data.compareTo(data) > 0) {
                temp = temp.leftChild;
            } else {
                temp = temp.rightChild;
            }
        }
        return null;
    }

    /**
     * 查找节点的父节点
     *
     * @param data
     * @return
     */
    public Node findParent(T data) {
        //从根节点开始遍历
        Node temp = root;
        Node prev = temp;
        while (temp != null) {
            //跳出循环时，temp 为 null，prev记录上一个节点，即为parent
            prev = temp;
            if (temp.data.compareTo(data) > 0) {
                temp = temp.leftChild;
            } else {
                temp = temp.rightChild;
            }
        }
        return prev;
    }

    /**
     * 左右分隔节点
     *
     * @param data
     * @return
     */
    public Node split(T data) {
        //找到节点
        Node node = getNode(data);
        //找到左节点的最大数节点
        Node big = getBig(node.leftChild);
        //将要分割节点的右节点的parent指向big
        node.rightChild.parent = big;
        //将big的右节点指向node的右节点
        big.rightChild = node.rightChild;
        return node.leftChild;
    }

    /**
     * 获取最大节点
     *
     * @param node
     * @return
     */
    public Node getBig(Node node) {
        Node temp = node;
        while (temp != null) {
            if (temp.rightChild != null) {
                temp = temp.rightChild;
            } else {
                return temp;
            }
        }
        return null;
    }

    /**
     * 创建二叉树
     * 
     * @param list
     * @return
     */
    public static BinaryTree createBinaryTree(List<Integer> list) {
        BinaryTree<Integer> binaryTree = new BinaryTree();
        for (Integer integer : list) {
            binaryTree.add(integer);
        }
        return binaryTree;
    }

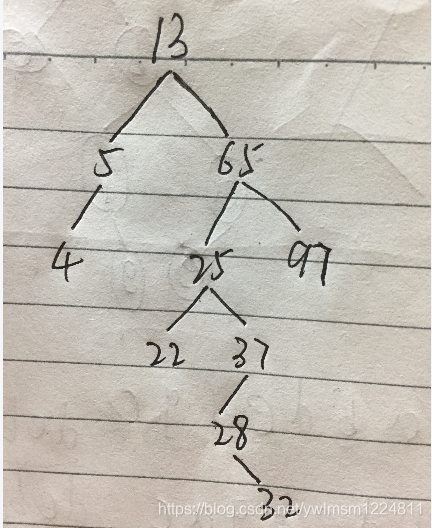
创建二叉树测试代码：

/**
 * 二叉树测试
 **/
public class BinaryTreeTest {
    private BinaryTree createBinaryTree() {
        List<Integer> list = Arrays.asList(13, 65, 5, 97, 25, 37, 22, 4, 28, 32);
        return BinaryTree.createBinaryTree(list);
    }

    @Test
    public void createBinaryTreeTest() {
        BinaryTree binaryTree = createBinaryTree();
    }

}

生成的二叉树如下图所示：

递归和非递归查询二叉树高度（深度）

 /**
     * 递归获取二叉树深度
     *
     * @return
     */
    public int recursiveGetTreeHight(Node root) {
        if (root == null) {
            return 0;
        }
        int leftHight = recursiveGetTreeHight(root.leftChild);
        int rightHight = recursiveGetTreeHight(root.rightChild);
        return leftHight >= rightHight ? leftHight + 1 : rightHight + 1;
    }

    /**
     * 非递归获取二叉树深度(广度遍历)
     * <p>
     * 思想：从根节点开始逐层遍历，每遍历完一层，层数+1
     *
     * @return
     */
    public int normalGetTreeHight(Node root) {
        if (root == null) {
            return 0;
        }
        // levelCount 每层节点总数，cursorIndex 当前层访问到的节点个数
        int levelCount, cursorIndex;
        Queue<Node> queue = new LinkedList<>();
        // 先将根节点放入链表list中
        queue.offer(root);
        // 二叉树高度
        int hight = 0;
        // 遍历的当前节点
        Node currentNode;
        while (!queue.isEmpty()) {
            cursorIndex = 0;
            levelCount = queue.size();
            while (cursorIndex < levelCount) {
                cursorIndex++;
                currentNode = queue.poll();
                if (currentNode.leftChild != null) {
                    queue.offer(currentNode.leftChild);
                }
                if (currentNode.rightChild != null) {
                    queue.offer(currentNode.rightChild);
                }
            }
            // 遍历完一层，层数+1
            hight++;
        }
        return hight;
    }

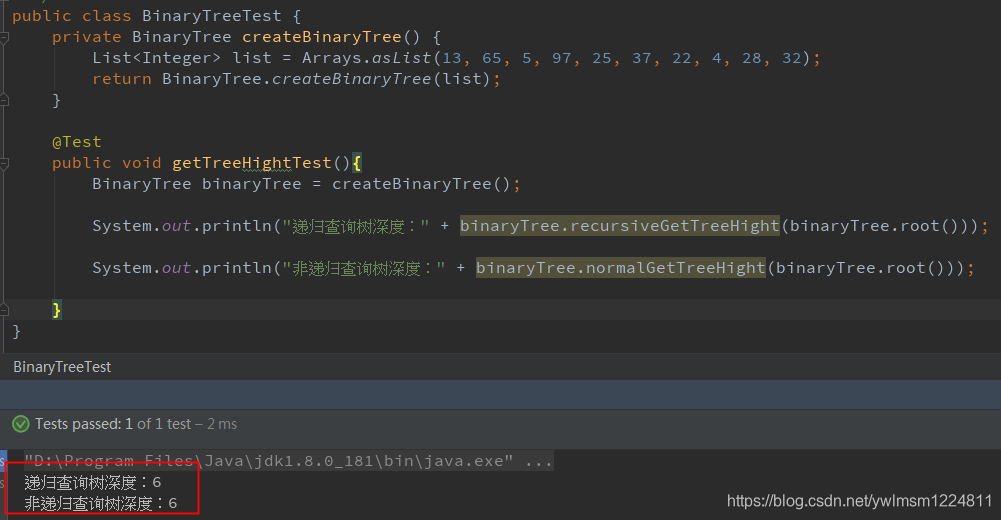
查询二叉树高度（深度）测试代码：

/**
 * 二叉树测试
 **/
public class BinaryTreeTest {
    private BinaryTree createBinaryTree() {
        List<Integer> list = Arrays.asList(13, 65, 5, 97, 25, 37, 22, 4, 28, 32);
        return BinaryTree.createBinaryTree(list);
    }

    @Test
    public void getTreeHightTest(){
        BinaryTree binaryTree = createBinaryTree();

        System.out.println("递归查询树深度：" + binaryTree.recursiveGetTreeHight(binaryTree.root()));

        System.out.println("非递归查询树深度：" + binaryTree.normalGetTreeHight(binaryTree.root()));

    }
}

运行结果：

二叉树的前中后序遍历

/**
     * 前序遍历（即深度遍历）（中->左->右）
     *
     * @param node
     */
    public void preOrder(Node node) {
        if (node != null) {
            System.out.print(node.data + ",");
            preOrder(node.leftChild);
            preOrder(node.rightChild);
        }
    }

    /**
     * 中序遍历（即深度遍历）（左->中->右）
     *
     * @param node
     */
    public void middleOrder(Node node) {
        if (node != null) {
            middleOrder(node.leftChild);
            System.out.print(node.data + ",");
            middleOrder(node.rightChild);
        }
    }

    /**
     * 后序遍历（即深度遍历）（左->右->中）
     *
     * @param node
     */
    public void afterOrder(Node node) {
        if (node != null) {
            afterOrder(node.leftChild);
            afterOrder(node.rightChild);
            System.out.print(node.data + ",");
        }
    }

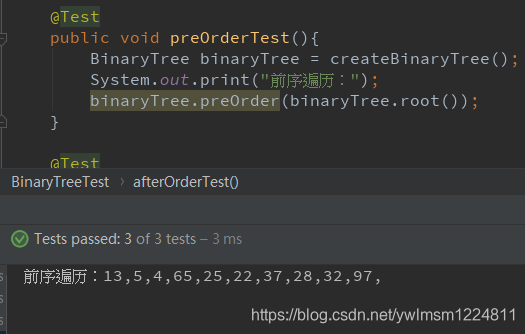
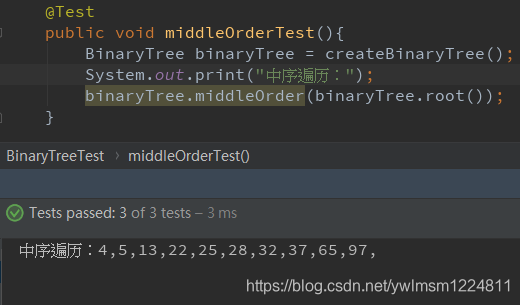
二叉树的前中后序遍历测试代码：

/**
 * 二叉树测试
 **/
public class BinaryTreeTest {
    private BinaryTree createBinaryTree() {
        List<Integer> list = Arrays.asList(13, 65, 5, 97, 25, 37, 22, 4, 28, 32);
        return BinaryTree.createBinaryTree(list);
    }

    @Test
    public void preOrderTest(){
        BinaryTree binaryTree = createBinaryTree();
        System.out.print("前序遍历：");
        binaryTree.preOrder(binaryTree.root());
    }

    @Test
    public void middleOrderTest(){
        BinaryTree binaryTree = createBinaryTree();
        System.out.print("中序遍历：");
        binaryTree.middleOrder(binaryTree.root());
    }

    @Test
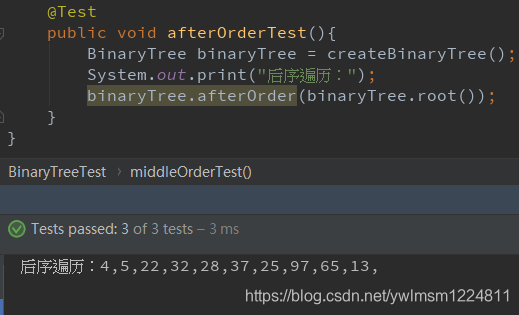
    public void afterOrderTest(){
        BinaryTree binaryTree = createBinaryTree();
        System.out.print("后序遍历：");
        binaryTree.afterOrder(binaryTree.root());
    }
}

运行结果：

前序遍历：13,5,4,65,25,22,37,28,32,97,

中序遍历：4,5,13,22,25,28,32,37,65,97,

后序遍历：4,5,22,32,28,37,25,97,65,13,

如下图所示：

递归和非递归深度优先遍历

/**
     * 非递归深度优先遍历，采用栈实现（先进后出）
     * <p>
     * 思想：沿着某一个分支一直遍历到底，利用此特点可以使用栈，先将右节点入栈、然后再左节点入栈，这样子出栈就是先左节点然后右节点
     *
     * @param root
     */
    public void depthFirstSearch(Node root) {
        if (root == null) {
            return;
        }
        Stack<Node> stack = new Stack<>();
        stack.push(root);
        Node currentNode;
        while (!stack.empty()) {
            currentNode = stack.pop();
            System.out.print(currentNode.data + ",");
            if (currentNode.rightChild != null) {
                stack.push(currentNode.rightChild);
            }
            if (currentNode.leftChild != null) {
                stack.push(currentNode.leftChild);
            }
        }
    }

    /**
     * 递归深度优先遍历，采用栈实现（先进后出）
     * <p>
     * 思想：沿着某一个分支一直遍历到底，利用此特点可以使用栈，先将右节点入栈、然后再左节点入栈，这样子出栈就是先左节点然后右节点
     *
     * @param root
     */
    public void recursionDepthFirstSearch(Node root) {
        if (root == null) {
            return;
        }
        System.out.print(root.data + ",");
        recursionDepthFirstSearch(root.leftChild);
        recursionDepthFirstSearch(root.rightChild);
    }

深度优先遍历测试代码：

/**
 * 二叉树测试
 **/
public class BinaryTreeTest {
    private BinaryTree createBinaryTree() {
        List<Integer> list = Arrays.asList(13, 65, 5, 97, 25, 37, 22, 4, 28, 32);
        return BinaryTree.createBinaryTree(list);
    }

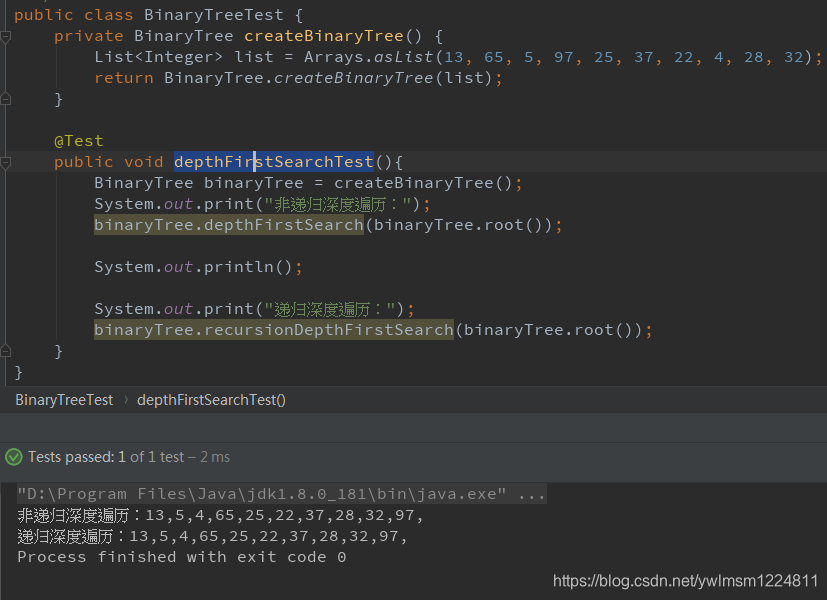
    @Test
    public void depthFirstSearchTest(){
        BinaryTree binaryTree = createBinaryTree();
        System.out.print("非递归深度遍历：");
        binaryTree.depthFirstSearch(binaryTree.root());

        System.out.println();

        System.out.print("递归深度遍历：");
        binaryTree.recursionDepthFirstSearch(binaryTree.root());
    }
}

运行结果：

广度优先遍历

/**
     * 广度优先遍历，采用队列实现（先进先出）
     * <p>
     * 思想：从左到右一层层的遍历,先往队列中插入左节点，再插右节点，这样出队就是先左后右了
     *
     * @param root
     */
    public void breadthFirstSearch(Node root) {
        if (root == null) {
            return;
        }

        Queue<Node> queue = new LinkedList<>();
        queue.offer(root);
        Node currentNode;
        while (!queue.isEmpty()) {
            currentNode = queue.poll();
            System.out.print(currentNode.data + ",");
            if (currentNode.leftChild != null) {
                queue.offer(currentNode.leftChild);
            }
            if (currentNode.rightChild != null) {
                queue.offer(currentNode.rightChild);
            }
        }
    }

广度优先遍历测试代码：

/**
 * 二叉树测试
 **/
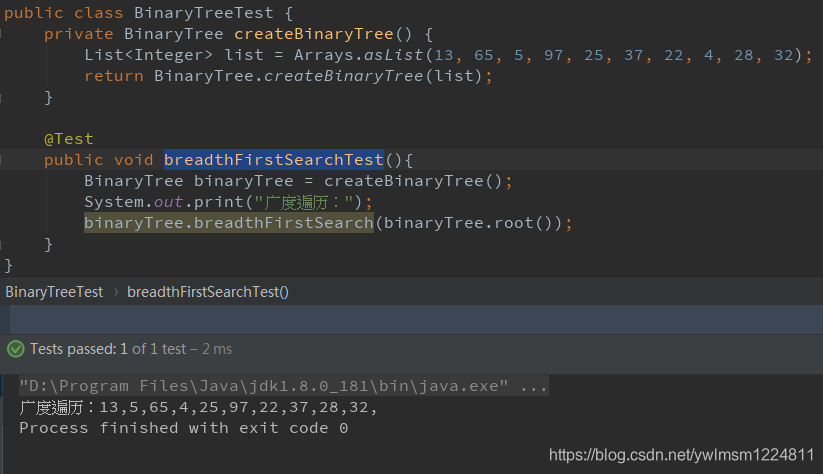
public class BinaryTreeTest {
    private BinaryTree createBinaryTree() {
        List<Integer> list = Arrays.asList(13, 65, 5, 97, 25, 37, 22, 4, 28, 32);
        return BinaryTree.createBinaryTree(list);
    }

    @Test
    public void breadthFirstSearchTest(){
        BinaryTree binaryTree = createBinaryTree();
        System.out.print("广度遍历：");
        binaryTree.breadthFirstSearch(binaryTree.root());
    }
}

运行结果：