冒(冒泡)择(选择)路(入:插入)兮(希尔)快(快速)归(归并)堆
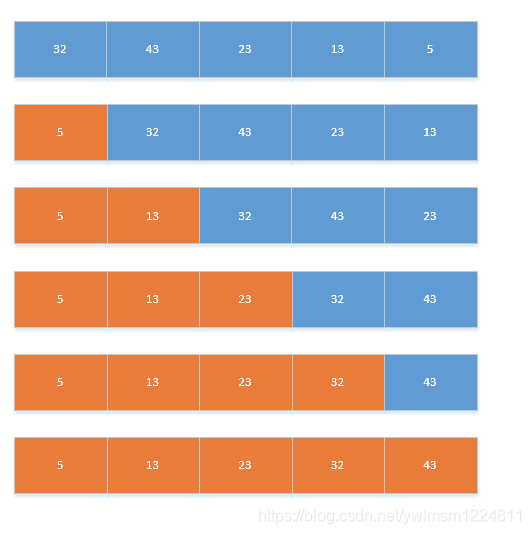
一、直接插入排序
经常碰到这样一类排序问题:把新的数据插入到已经排好的数据列中
1、首先设定插入次数,即循环次数,for(int i=1;i < length;i++),1个数的那次不用插入
2、设定插入数和已经得到排好序列的最后一位数的位置,即insertNum 和 j = i -1
3、从最后一个数开始向前循环,如果插入数小于当前数,就将当前数向后移动一位
// 直接插入排序
public void insertSort(int a[]){
// 数组长度,将这个提取出来是为了提高速度
int length = a.length;
// 要插入的数
int insertNum;
// 要插入的次数
for (int i =1; i < length; i++){
// 要插入的数
insertNum = a[i];
// 已经排好序的元素个数
int j = i - 1;
while (j >= 0 && a[j] > insertNum){
// 从后往前循环,将大于insertNum的数向后移动一位
a[j+1] = a[j];
j--;
}
//将需要插入的数放在要插入的位置
a[j+1] = insertNum;
}
}
二、希尔排序
1、将数的个数设为n,取奇数k=n/2,将下标差值为k的数分为一组,构成有序序列。
2、再取k=k/2 ,将下标差值为k的数分为一组,构成有序序列。
3、然后将 length / 2,重复1、2步骤,直到 length = 0 为止
// 希尔排序
public void sheelSort(int a[]){
int d = a.length;
while(d != 0){
d = d / 2;
// 分的组数
for(int x = 0; x < d; x++){
// 组中的元素,从第二个数开始算起
for(int i = x + d; i < a.length; i += d){
// j 为有序序列最后一位的位置
int j = i - d;
// 要插入的元素
int temp = a[i];
while( j >= 0 && a[j] > temp){
// 向后移动d位
a[j+d] = a[j];
j -= d;
}
a[j+d] = temp;
}
}
}
}
三、简单选择排序
(如果每次比较都交换,那么就是交换排序(冒泡排序);如果每次比较完一个循环再交换,就是简单选择排序。)
2、将当前位置后面所有的数与当前位置数比较,较小数赋值给 key,并记住较小数的位置
// 简单选择排序
public void selectSort(int a[]){
int length = a.length;
// 循环次数
for(int i = 0; i < length-1; i++){
// 记录要比较的值
int key = a[i];
// 记录比较的位置
int position = i;
for(int j = i+1; j < length; j++){
if(key > a[j]){
// 循环找出最小数以及对应的位置
key = a[j];
position = j;
}
}
// 交换位置
a[position] = a[i];
a[i] = key;
}
}
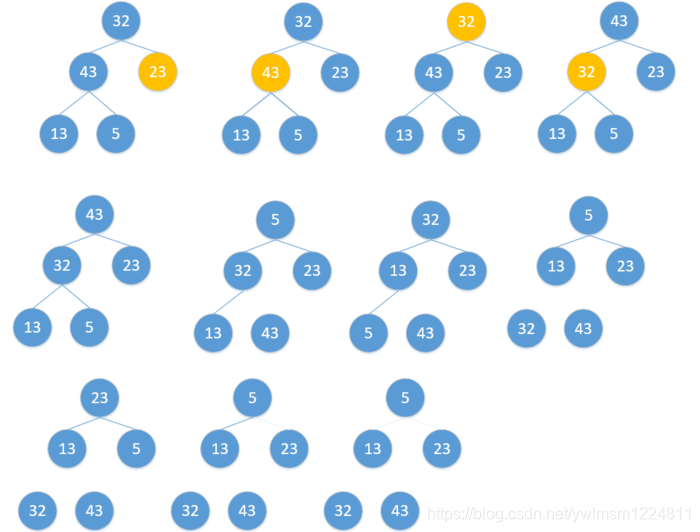
// 堆排序
public void heapSort(int[] a){
int arrayLength=a.length;
//循环建堆
for(int i=0;i<arrayLength-1;i++){
//建堆
buildMaxHeap(a,arrayLength-1-i);
//交换堆顶和最后一个元素
swap(a,0,arrayLength-1-i);
System.out.println(Arrays.toString(a));
}
}
// 交换数据
private void swap(int[] data, int i, int j) {
int tmp=data[i];
data[i]=data[j];
data[j]=tmp;
}
//对data数组从0到lastIndex建大顶堆
private void buildMaxHeap(int[] data, int lastIndex) {
//从lastIndex处节点(最后一个节点)的父节点开始
for(int i=(lastIndex-1)/2;i>=0;i--){
//k保存正在判断的节点
int k=i;
//如果当前k节点的子节点存在
while(k*2+1<=lastIndex){
//k节点的左子节点的索引
int biggerIndex=2*k+1;
//如果biggerIndex小于lastIndex,即biggerIndex+1代表的k节点的右子节点存在
if(biggerIndex<lastIndex){
//若果右子节点的值较大
if(data[biggerIndex]<data[biggerIndex+1]){
//biggerIndex总是记录较大子节点的索引
biggerIndex++;
}
}
//如果k节点的值小于其较大的子节点的值
if(data[k]<data[biggerIndex]){
//交换他们
swap(data,k,biggerIndex);
//将biggerIndex赋予k,开始while循环的下一次循环,重新保证k节点的值大于其左右子节点的值
k=biggerIndex;
}else{
break;
}
}
}
}
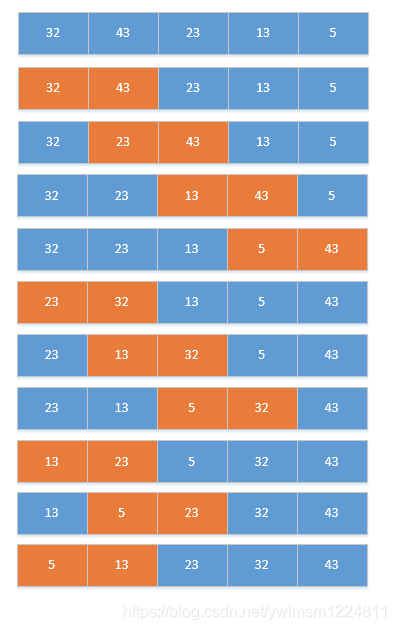
五、冒泡排序
// 冒泡排序
public void bubbleSort(int[] a){
// 按照最小的找出
int lenght = a.length;
int temp;
for(int i = 0; i < lenght-1 ; i++){
for(int j=i+1; j < lenght; j++){
if(a[i] > a[j]){
temp = a[j];
a[j] = a[i];
a[i] = temp;
}
}
}
// 按照最大的找出
int length=a.length;
int temp;
for(int i=0;i<length;i++){
for(int j=0;j<length-i-1;j++){
if(a[j]>a[j+1]){
temp=a[j];
a[j]=a[j+1];
a[j+1]=temp;
}
}
}
}
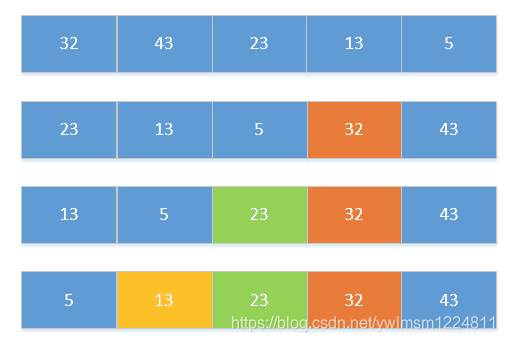
六、快速排序
1、选择第一个数为p,小于p的数放在左边,大于p的数放在右边。
2、递归的将p左边和右边的数都按照第一步进行,直到不能递归。
// 快速排序
public void quickSort(int a[], int start, int end){
if(start < end){
// 第一个数作为基准值
int base = a[start];
// 临时中间值
int temp;
int i = start, j = end;
do {
while (a[i] < base && i < end){
// 找出比基数小的数位置
i++;
}
while (a[j] > base && j > start){
// 找出比基数大的位置
j--;
}
if(i <= j){
temp = a[i];
a[i] = a[j];
a[j] = temp;
i++;
j--;
}
} while (i <= j);
if (start < j) {
quickSort(a, start, j);
}
if (end > i) {
quickSort(a, i, end);
}
}
}
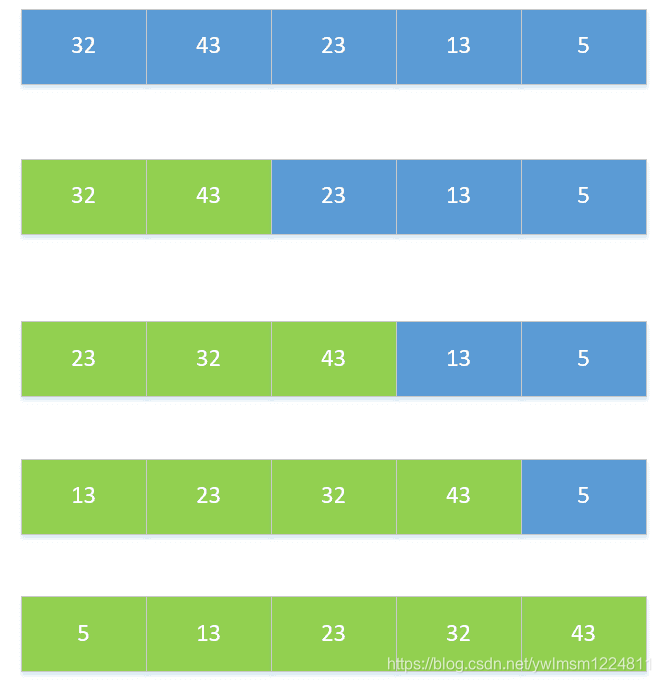
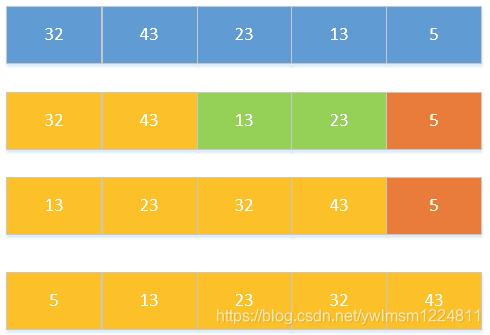
七、归并排序
速度仅次于快排,内存少的时候使用,可以进行并行计算的时候使用。
demo示例:
/**
* 归并排序
*
* <p>
* 算法思想:
* <p>
* 速度仅次于快排,内存少的时候使用,可以进行并行计算的时候使用。
* <p>
* 1、选择相邻两个数组成一个有序序列。
* <p>
* 2、选择相邻的两个有序序列组成一个有序序列。
* <p>
* 3、重复第二步,直到全部组成一个有序序列。
*
* @date 2019-12-12 17:14
**/
public class MergeSort {
public static void mergeSort(int[] a, int low, int high) {
if (low < high) {
// 防止溢出,(high + low) / 2 这种写法有溢出的漏洞
int mid = low + (high - low) / 2;
// 或者使用无符号右移方式
// int mid = (high + low) >>> 2;
// 左边
mergeSort(a, low, mid);
// 右边
mergeSort(a, mid + 1, high);
// 左右边数据排序后合并
sortMerge(a, low, mid, high);
}
}
private static void sortMerge(int[] a, int low, int mid, int high) {
// 临时存放排序后的数据
int[] temp = new int[high - low + 1];
// 临时数组temp存放数的位置
int index = 0;
// 左半边指针
int i = low;
// 右半边指针
int j = mid + 1;
while (i <= mid && j <= high) {
if (a[i] >= a[j]) {
// temp 存放右边的较小值
temp[index++] = a[j++];
} else {
// temp 存放左边的较小值
temp[index++] = a[i++];
}
}
while (i <= mid) {
// 左边剩余的数据
temp[index++] = a[i++];
}
while (j <= high) {
// 右边剩余的数据
temp[index++] = a[j++];
}
for (int x = 0; x < temp.length; x++) {
// 排好序的数组赋值给原数组a
a[low + x] = temp[x];
}
}
}
排序算法分类、稳定性以及复杂度
1)、分类
插入排序:插入排序、希尔排序
选择排序:简单选择排序、堆排序
交换排序:冒泡排序、快速排序
归并排序
基数排序
2)、稳定性:
稳定:冒泡排序、插入排序、归并排序和基数排序
不稳定:选择排序、快速排序、希尔排序、堆排序
3)、平均时间复杂度
O(n^2):直接插入排序,简单选择排序,冒泡排序。
在数据规模较小时(9W内),直接插入排序,简单选择排序差不多。当数据较大时,冒泡排序算法的时间代价最高。性能为O(n^2)的算法基本上是相邻元素进行比较,基本上都是稳定的。
O(nlogn):快速排序,归并排序,希尔排序,堆排序。
其中,快排是最好的, 其次是归并和希尔,堆排序在数据量很大时效果明显。
4)、排序算法的选择
1.数据规模较小
(1)待排序列基本序的情况下,可以选择直接插入排序;
(2)对稳定性不作要求宜用简单选择排序,对稳定性有要求宜用插入或冒泡
2.数据规模不是很大
(1)完全可以用内存空间,序列杂乱无序,对稳定性没有要求,快速排序,此时要付出log(N)的额外空间。
(2)序列本身可能有序,对稳定性有要求,空间允许下,宜用归并排序
3.数据规模很大
(1)对稳定性有求,则可考虑归并排序。
(2)对稳定性没要求,宜用堆排序
4.序列初始基本有序(正序),宜用直接插入,冒泡
各算法复杂度如下:
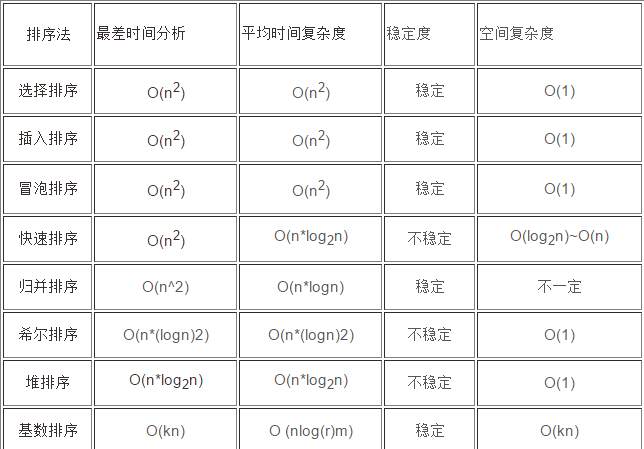








 本文介绍了多种排序算法,包括直接插入排序、希尔排序、简单选择排序、堆排序、冒泡排序、快速排序和归并排序,阐述了各算法的思想和实现步骤,还对排序算法进行了分类,分析了稳定性和平均时间复杂度,并给出了不同数据规模下排序算法的选择建议。
本文介绍了多种排序算法,包括直接插入排序、希尔排序、简单选择排序、堆排序、冒泡排序、快速排序和归并排序,阐述了各算法的思想和实现步骤,还对排序算法进行了分类,分析了稳定性和平均时间复杂度,并给出了不同数据规模下排序算法的选择建议。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








