果园里的树

最新推荐文章于 2025-12-27 16:49:17 发布

原创最新推荐文章于 2025-12-27 16:49:17 发布 · 341 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#几何学 #算法

算法专栏收录该内容

3 篇文章

订阅专栏

本文介绍了一种通过计算三角形有向面积判断点是否在三角形内的算法，用于解决果园树计数问题。该方法避免了复杂的浮点运算，提高了算法的准确性和效率。

果园里的树

——选自《算法竞赛入门经典》
最近看了点《算法竞赛入门经典》，看到数学基础这一部分，感觉果园里的树这一题挺有意思的，就想记录一下。

1.问题描述

果园里的树排列成矩阵。它们的x和y坐标均是1~99的整数。输入若干个三角形，依次统计每一个三角形内部和边界上共有多少棵树，如下图所示。
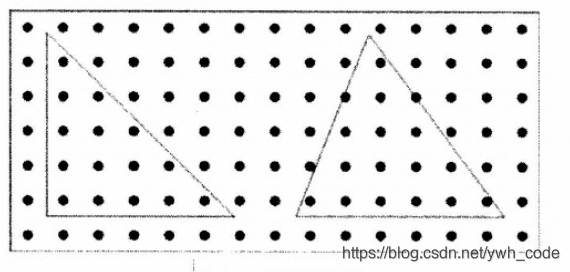
在这里插入图片描述

2.问题分析

最容易想到的一个方法就是逐一判断：对于每个点(x,y)，看看它是否在三角形内。为此，我们来看这样一个函数：

double area(double x0, double y0, double x1, double y1, double x2, double y2){
	return x0*y1+x2*y0+x1*y2-x2*y1-x0*y2-x1*y0;
}

它给出了三角形(x0,y0)—(x1,y1)—(x2,y2)的有向面积(signed area)的两倍。上面的公式可以借助行列式进行记忆：
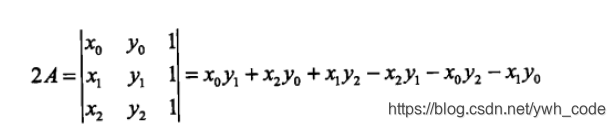
在这里插入图片描述
有了它之后，判断起来就很简单了：假设输入的三角形为ABC，待判断的点为O，则O在三角形ABC的内部或边界上当且仅当S_ABC = S_OAB + S_OBC + S_OCA。

3.注意注意注意

感觉书中的这一部分提到的才是要学习的。

在判断两个浮点数a和b是否相等时，请尽量判断fabs(a-b)是否小于一个事先给定的eps，如1e-9。
如果可能，请尽量避免浮点运算（即使输入浮点数，如果规定只保留两位小数，也可以给该浮点数乘以100，转化为整数）。
在该题中，有人可能有人会想到使用海伦公式。由于涉及到浮点的运算，因此作者建议尽量避免。