CH2 马尔科夫决策过程(Markov Decision Processes)
文章目录
1 马尔科夫过程(Markov Processes)
马尔科夫决策过程描述的是完全可知的环境。
1.1 马尔科夫的性质
1️⃣状态转移概率与状态转移矩阵
马尔科夫过程的当前状态完全可描述此过程,其满足:
P [ S t + 1 ∣ S t ] = P [ S t + 1 ∣ S 1 , . . . , S t ] P[S_{t+1}|S_{t}]=P[S_{t+1}|S_1,...,S_t] P[St+1∣St]=P[St+1∣S1,...,St]
S t S_t St:t时刻处于状态S
状态转移概率(the state transition probability):t时刻位于状态S,而(t+1)时刻位于状态s’的概率
P s s ′ = P [ S t + 1 = s ′ ∣ S t = s ] P_{ss'}=P[S_{t+1}=s'|S_t=s] Pss′=P[St+1=s′∣St=s]
状态转移矩阵(State transition matrix):

注意: ∑ j P i j = 1 \sum_{j}P_{ij}=1 ∑jPij=1
1.2 马尔科夫链(无记忆过程)
马尔科夫过程可描述为二元组<状态,状态转移矩阵>,表示为 < S , P > <S,P> <S,P>
2 马尔科夫奖励过程 (Markov Reward Processes)
2.1 MRP
马尔科夫奖励过程可表述为四元组<状态,状态转移概率矩阵,奖励函数,折扣因子>,表示为 < S , P , R , γ > <S,P,R,\gamma> <S,P,R,γ>
-
S S S:一系列状态
-
P P P:状态转移概率矩阵
-
R R R:奖励函数(reward function), R s R_s Rs表示状态为 S t S_t St时的下一时刻(t+1)的奖励 R t + 1 R_{t+1} Rt+1的期望(可由人为设定)
R s = E [ R t + 1 ∣ S t = s ] R_s=E[R_{t+1}|S_t=s] Rs=E[Rt+1∣St=s]
-
γ \gamma γ:折扣因子(discount factor) γ ∈ [ 0 , 1 ] \gamma \in[0,1] γ∈[0,1]
2.2 回报(Return)
回报 G t G_t Gt: 时刻t 往后走的总折扣奖励
G t = R t + 1 + γ R t + 2 + . . . = ∑ k = 0 ∞ γ k R t + k + 1 G_t=R_{t+1}+\gamma R_{t+2}+...=\sum_{k=0}^{\infty}\gamma^k R_{t+k+1} Gt=Rt+1+γRt+2+...=k=0∑∞γkRt+k+1
-
γ − > 0 \gamma->0 γ−>0: 短视(myopic),回报只与下一时刻的奖励有关
-
γ − > 1 \gamma->1 γ−>1: 远视(far-sighted), 回报与往后每一时刻的奖励均有关
-
折扣因子 γ \gamma γ的作用:
- 数学计算便利;避免在环形马尔科夫链中出现无限循环;
- 在经济方面,即时奖励比延时奖励更有收益
2.3 值函数(Value Function)
值函数 v ( s ) v(s) v(s): 状态s的长期价值 v ( s ) = E [ G t ∣ S t = s ] v(s)=E[G_t|S_t=s] v(s)=E[Gt∣St=s]
2.4 贝尔曼方程(Bellman equation)
贝尔曼方程:(线性方程)
v
=
R
+
γ
P
v
v
=
(
1
−
γ
P
)
−
1
R
v = R+\gamma Pv\\ v = (1-\gamma P)^{-1}R
v=R+γPvv=(1−γP)−1R
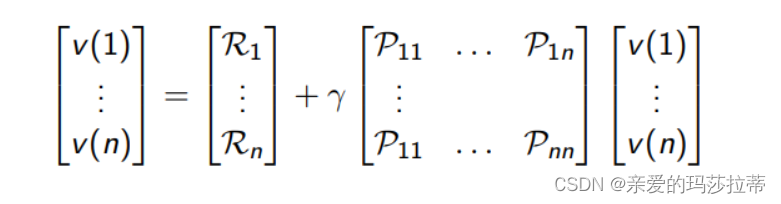
v:值函数 γ \gamma γ:折扣因子 P P P:状态转移概率矩阵 R:状态即时奖励
推导:
v
(
s
)
v(s)
v(s)可由下一状态的值函数
v
(
S
t
+
1
)
v(S_{t+1})
v(St+1)即
v
(
s
′
)
v(s')
v(s′)表示:
v
(
s
)
=
E
[
G
t
∣
S
t
=
s
]
=
E
[
R
t
+
1
+
γ
R
t
+
2
+
γ
2
R
t
+
3
.
.
.
∣
S
t
=
s
]
=
E
[
R
t
+
1
+
γ
(
R
t
+
2
+
γ
R
t
+
3
)
.
.
.
∣
S
t
=
s
]
=
E
[
R
t
+
1
+
γ
(
G
t
+
1
)
∣
S
t
=
s
]
=
E
[
R
t
+
1
+
γ
(
v
(
S
t
+
1
)
∣
S
t
=
s
]
\boldsymbol{v(s)}=E[G_t|S_t=s]\\ =E[R_{t+1}+\gamma R_{t+2}+\gamma^2 R_{t+3}...|S_t=s]\\ =E[R_{t+1}+\gamma (R_{t+2}+\gamma R_{t+3})...|S_t=s]\\ =E[R_{t+1}+\gamma (G_{t+1})|S_t=s]\\ =E[R_{t+1}+\gamma (\boldsymbol{v(S_{t+1})}|S_t=s]
v(s)=E[Gt∣St=s]=E[Rt+1+γRt+2+γ2Rt+3...∣St=s]=E[Rt+1+γ(Rt+2+γRt+3)...∣St=s]=E[Rt+1+γ(Gt+1)∣St=s]=E[Rt+1+γ(v(St+1)∣St=s]
即可得:
v
(
s
)
=
R
s
+
γ
∑
s
′
∈
S
P
s
s
′
v
(
s
′
)
\boldsymbol{v(s)=R_s+\gamma\sum_{s'\in S}P_{ss'}v(s')}
v(s)=Rs+γs′∈S∑Pss′v(s′)
即当前状态s的值函数等于该状态的即时奖励
R
s
R_s
Rs 加上下一可能状态的延时值函数的加权平均。
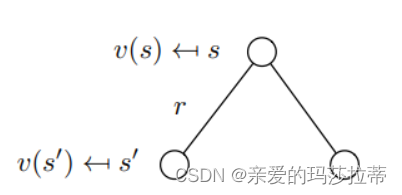
注意:s’不止一个!!!
- 贝尔曼方程求解的复杂度为 O ( n 3 ) O(n^3) O(n3),n为状态数
- 贝尔曼方程只适合小的MRP
- 大型MRP推荐方法:动态规划(模型完全已知)、蒙特卡洛估计(模型未知)、TD迭代
3 马尔科夫决策过程(Markov Decision Processes)
3.1 马尔科夫决策过程MDP
马尔科夫决策过程可表述为五元组<状态,动作,状态转移概率矩阵,奖励函数,折扣因子>,表示为 < S , A , P , R , γ > <S,A,P,R,\gamma> <S,A,P,R,γ>
-
S S S:一系列状态
-
A A A:一系列动作
-
P P P:状态转移概率矩阵 P s s ′ a P_{ss'}^a Pss′a:状态s经过动作a到达状态s’
P s s ′ a = P [ S t + 1 = s ′ ∣ S t = s , A t = a ] P_{ss'}^a=P[S_{t+1}=s'|S_t=s,A_t=a] Pss′a=P[St+1=s′∣St=s,At=a]
-
R R R:奖励函数(reward function), R s R_s Rs表示状态为 S t S_t St时的经过动作a到达下一时刻(t+1)的奖励 R t + 1 R_{t+1} Rt+1的期望(可由人为设定)
R s = E [ R t + 1 ∣ S t = s , A t = a ] R_s=E[R_{t+1}|S_t=s,A_t=a] Rs=E[Rt+1∣St=s,At=a]
-
γ \gamma γ:折扣因子(discount factor) $
3.2 策略Policy
策略是指在什么状态下执行什么动作,策略与时间无关
策略 π \pi π: π ( a ∣ s ) = P [ A t = a ∣ S t = s ] \pi(a|s)=P[A_t=a|S_t=s] π(a∣s)=P[At=a∣St=s]
3.3 加上策略的MDP
五元组 < S , A , P π , R π , γ > <S,A,P^{\pi},R^{\pi},\gamma> <S,A,Pπ,Rπ,γ>
| 表示 | 计算式 | 含义 |
|---|---|---|
| P s , s ′ π P^{\pi}_{s,s'} Ps,s′π | P s , s ′ π = ∑ a ∈ A π ( a ∣ s ) P s , s ′ a P^{\pi}_{s,s'}=\sum_{a\in A}\pi(a|s)P^{a}_{s,s'} Ps,s′π=∑a∈Aπ(a∣s)Ps,s′a | 策略π的状态转移概率为状态s做动作a的概率*做动作a到状态s’的概率 |
| R s π R^{\pi}_{s} Rsπ | R s π = ∑ a ∈ A π ( a ∣ s ) R s a R^{\pi}_{s}=\sum_{a\in A}\pi(a|s)R^{a}_{s} Rsπ=∑a∈Aπ(a∣s)Rsa | 策略π的奖励为状态s做所有动作到状态s’的奖励的加权平均 |
| v π ( s ) v_{\pi}(s) vπ(s) | v π ( s ) = E π [ G t ∣ S t = s ] v π ( s ) = E π [ R t + 1 + γ v π ( S t + 1 ) ∣ S t = s ] v_{\pi}(s)=E_{\pi}[G_t|S_t=s]\\v_{\pi}(s)=E_{\pi}[R_{t+1}+\gamma v_{\pi}(S_{t+1})|S_t=s] vπ(s)=Eπ[Gt∣St=s]vπ(s)=Eπ[Rt+1+γvπ(St+1)∣St=s] | 策略π的状态价值函数为状态s下做策略π的收益 |
| q π ( s , a ) q_{\pi}(s,a) qπ(s,a) | q π ( s , a ) = E π [ G t ∣ S t = s , A t = a ] q π ( s , a ) = E π [ R t + 1 + γ q π ( S t + 1 , A t + 1 ) ∣ S t = s , A t = a ) q_{\pi}(s,a)=E_{\pi}[G_t|S_t=s,A_t=a]\\q_{\pi}(s,a)=E_{\pi}[R_{t+1}+\gamma q_{\pi}(S_{t+1},A_{t+1})|S_t=s,A_t=a) qπ(s,a)=Eπ[Gt∣St=s,At=a]qπ(s,a)=Eπ[Rt+1+γqπ(St+1,At+1)∣St=s,At=a) | 状态动作价值函数为状态s下,执行动作a,继续遵循策略π的收益 |
注意: v π ( s ) = ∑ a ∈ A π ( a ∣ s ) q π ( s , a ) v_{\pi}(s)=\sum_{a\in A}\pi(a|s)q_{\pi}(s,a) vπ(s)=∑a∈Aπ(a∣s)qπ(s,a)

q π ( s , a ) = R s a + γ ∑ s ′ ∈ S P s s ′ a v π ( s ′ ) q_{\pi}(s,a)=R_s^a+\gamma\sum_{s'\in S}P^a_{ss'}v_{\pi}(s') qπ(s,a)=Rsa+γ∑s′∈SPss′avπ(s′)

v
π
(
s
)
=
∑
a
∈
A
π
(
a
∣
s
)
q
π
(
s
,
a
)
v
π
(
s
)
=
∑
a
∈
A
π
(
a
∣
s
)
(
R
s
a
+
γ
∑
s
′
∈
S
P
s
s
′
a
v
π
(
s
′
)
)
v_{\pi}(s)=\sum_{a\in A}\pi(a|s)q_{\pi}(s,a)\\ \boldsymbol{v_{\pi}(s)=\sum_{a\in A}\pi(a|s)(R_s^a+\gamma\sum_{s'\in S}P^a_{ss'}v_{\pi}(s'))}
vπ(s)=a∈A∑π(a∣s)qπ(s,a)vπ(s)=a∈A∑π(a∣s)(Rsa+γs′∈S∑Pss′avπ(s′))
注意:在状态s下,执行什么动作是不确定的,执行动作a后的状态s‘是不确定的。

贝尔曼方程:
v
π
=
R
π
+
γ
P
π
v
π
v
π
=
(
1
−
γ
P
π
)
−
1
R
π
v_{\pi} = R^{\pi}+\gamma P^{\pi}v_{\pi}\\ v_{\pi} = (1-\gamma P^{\pi})^{-1}R^{\pi}
vπ=Rπ+γPπvπvπ=(1−γPπ)−1Rπ








 本文深入介绍了马尔科夫过程、马尔科夫奖励过程及其在决策过程中的应用。讨论了状态转移概率、奖励函数、折扣因子的概念,并详细阐述了值函数与贝尔曼方程。最后,引入了策略在马尔科夫决策过程中的作用,探讨了带有策略的马尔科夫决策过程及其相关计算公式。
本文深入介绍了马尔科夫过程、马尔科夫奖励过程及其在决策过程中的应用。讨论了状态转移概率、奖励函数、折扣因子的概念,并详细阐述了值函数与贝尔曼方程。最后,引入了策略在马尔科夫决策过程中的作用,探讨了带有策略的马尔科夫决策过程及其相关计算公式。
















 424
424

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








