【数据结构和算法】常用基本算法汇总2 动态规划

原文参考自 头条 Java后端开发

动态规划

一、基本概念

每次决策依赖于当前状态，又随即引起状态的转移，一个决策序列就是在变化的状态中产生出来的，所以，这种多阶段最优化决策解决问题的过程就称为动态规划。

二、基本思想

基本思想：与分治法类似，也是将待求解的问题分解为若干个子问题，按顺序求解子问题，前一子问题的解，为后一子问题的求解提供了有用的信息。在求解任一子问题时，列出各种可能的局部解，通过决策保留那些有可能达到最优的局部解，丢弃其他局部 解，依次解决各子问题，最后一个子问题就是初始问题的解。

与分治法最大的差别：适合于用动态规划法求解的问题，经分解后得到的子问题往往不是互相独立的（即下一个子阶段的求解是建立在上一个子阶段的解的基础上，进行进一步的求解）。

三、适用的情况

（1）最优化原理：如果问题的最优解所包含的子问题的解也是最优的，就称该问题具有最优子结构，即满足最优化原理。

（2）无后效性：即某阶段状态一旦确定，就不受这个状态以后决策的影响，也就是说，某状态以后的过程不会影响以前的状态，只与当前状态有关。

（3）有重叠子问题：即子问题之间是不独立的，一个子问题在下一阶段决策中可能被多次使用到。（该性质并不是动态规划适用的必要条件，但是如果没有这条性质，动态规划算法同其他算法相比就不具备优势）

四、解题步骤

动态规划所处理的问题是一个多阶段决策问题，一般由初始状态开始，通过对中间阶段决策的选择，达到结束状态。这些决策形成了一个决策序列，同时确定了完成整个过程的一条活动路线(通常是求最优的活动路线)。动态规划的设计都有着一定的模式，一般要经历以下几个步骤：

初始状态→│决策１│→│决策２│→…→│决策ｎ│→结束状态

(1)划分阶段：按照问题的时间特征，把问题分为若干个阶段，在划分阶段时，注意划分后的阶段一定要是有序的或者是可排序的，否则问题就无法求解。

(2)确定状态和状态变量：将问题发展到各个阶段时所处于的各种客观情况用不同的状态表示出来，当然，状态的选择要满足无后效性。

(3)确定决策并写出状态转移方程：因为决策和状态转移有着天然的联系，状态转移就是根据上一阶段的状态和决策来导出本阶段的状态。所以如果确定了决策，状态转移方程也就可写出。但事实上常常是反过来做，根据相邻两个阶段的状态之间的关系来确定决策方法和状态转移方程。

(4)寻找边界条件：给出的状态转移方程是一个递推式，需要一个递推的终止条件或边界条件。

一般，只要解决问题的阶段、状态和状态转移决策确定了，就可以写出状态转移方程。实际应用中可以按以下几个简化的步骤进行设计：

（1）分析最优解的性质，并刻画其结构特征。

（2）递归的定义最优解。

（3）以自底向上或自顶向下的记忆化方式（备忘录法）计算出最优值。

（4）根据计算最优值时得到的信息，构造问题的最优解。

五、算法实现的说明

动态规划的主要难点在于上面4个步骤的确定，一旦设计完成，实现部分就会非常简单。使用动态规划求解问题，最重要的就是确定动态规划三要素：

（1）问题的阶段

（2）每个阶段的状态

（3）从前一个阶段转化到后一个阶段之间的递推关系。

递推关系必须是从次小的问题开始到较大的问题之间的转化，从这个角度来说，动态规划往往可以用递归程序来实现，不过因为递推可以充分利用前面保存的子问题的解来减少重复计算，所以对于大规模问题来说，有递归不可比拟的优势，这也是动态规划算法的核心之处。

确定了动态规划的这三要素，整个求解过程就可以用一个最优决策表来描述，最优决策表是一个二维表，其中行表示决策的阶段，列表示问题状态，表格需要填写的数据一般对应此问题的在某个阶段某个状态下的最优值（如最短路径，最长公共子序列，最大价值等），填表的过程就是根据递推关系，从1行1列开始，以行或者列优先的顺序，依次填写表格，最后根据整个表格的数据通过简单的取舍或者运算求得问题的最优解。

f(n,m)=max{f(n-1,m), f(n-1,m-w[n])+P(n,m)}

六、经典例子

• 孩子有多像爸爸--最长公共子序列：

c[i][j]表示Xi和Yi的最长公共子序列长度。

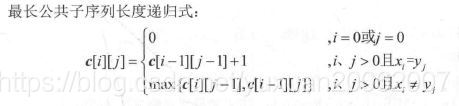
• DNA基因鉴定--编辑距离：

d[i][j]表示Xi和Yi的编辑距离。

• 长江一日游--游艇租赁:

这个题目要从规模d=3开始循环计算，为什么要这样呢？

其实也蛮容易理解的，为了求m[i][j] 要知道m[i][k]然后再求m[k][j]，这里要首先m[i][k]是最优解了，所以要一步一步先算出m[i][k]的最优解。

• 快速计算--矩阵连乘：

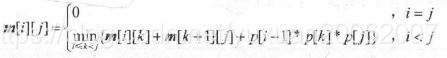
这个题目和之前的题目类似，问题的规模从2开始循环递增。

• 切披萨--最优三角刨分：

这个题目的数学建模有点复杂，转化成凸多边形和邻接矩阵就简单多了。

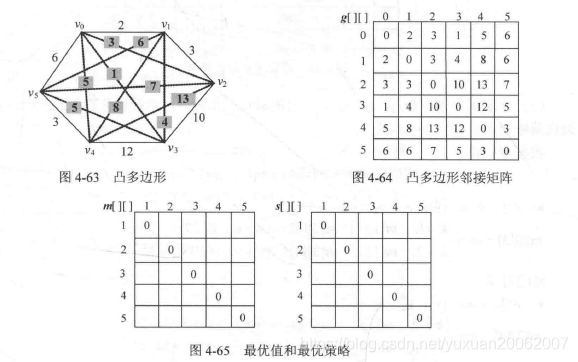
还有，最优三角刨分就是要三角刨分。

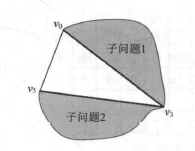
m[i][j]表示凸多边形从i-1顶点到j顶点的三角刨分的最优值（权值）

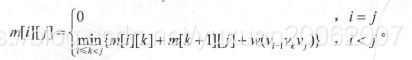
• 石子合并：

Min[i][j]代表从第i堆石子到第j堆石子的最小花费

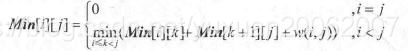
• 大卖场购物车1--0-1背包问题：

这个题目其实简化了，每个物品只有1个，要么放要么不放。

c[i][j]表示前i个物品放入一个容量位j的购物车可以获得的做大价值。

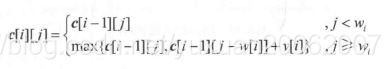
• 快速定位--最优二叉搜索树：

optimal binary search tree OBST

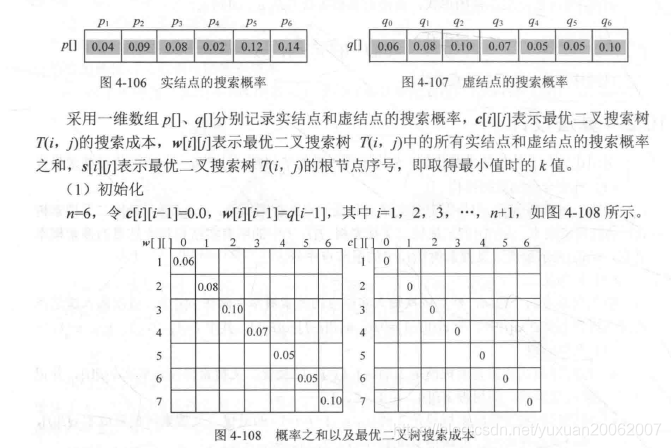
这个题目略难，其实难点就是在于建模。

最后写两个function，一个是optimal_BST，一个是construct_optimal_BST;

最后还有四边形不等式的优化，O（n^2）。四边形不等式优化讲解（详解）

七、算法秘籍

陈小玉老师在趣学算法里做了很好的总结：

动态规划求解最优化问题时需要考虑两个性质：最优子结构和子问题重叠，只要满足最优子结构性质就可以使用动态规划，如果还具有子问题重叠，则更能彰显动态规划的优势。判断可以使用动态规划后，就可以分析其最优子结构特征，找到原问题和子问题的关系，从而得到最优解递归式。然后按照最优解递归式自底向上求解，采用备忘机制(查表法)有效解决子问题重叠，重复的子问题不需要重复求解，只需查表即可。

动态规划的关键：

(1) 最优子结构判定

a. 作出一个选择；

b. 假定已经知道了哪种选择是最优的；

例如矩阵连乘问题，我们假设已经知道在第k个矩阵加括号是最优的，即(AiAi+1…Ak)(Ak+1Ak+2…Aj)。

c. 最优选择后会产生哪些子问题；

例如矩阵连乘问题，我们作出最优选择后产生两个子问题：(AiAi+1…Ak)，(Ak+1Ak+2…Aj)。

d. 证明原问题的最优解包含其子问题的最优解。

通常使用“剪切—粘贴”反证法。证明如果原问题的解是最优解，那么子问题的解也是最优解。反证：假定子问题的解不是最优解，那么就可以将它“剪切”掉，把最优解“粘贴”进去，从而得到一个比原问题最优解更优的解，这与前提原问题的解是最优解矛盾。得证。

例如：矩阵连乘问题，c=a+b+d，我们只需要证明如果c是最优的，则a和b一定是最优的（即原问题的最优解包含子问题的最优解）。

反证法：如果a不是最优的，(AiAi+1…Ak) 存在一个最优解aˊ，aˊ<a，那么，aˊ+b+d<c，这与假设c是最优的矛盾，因此如果c是最优的，则a一定是最优的。同理可证b也是最优的。因此如果c是最优的，则a和b一定是最优的。因此，矩阵连乘问题具有最优子结构性质。

(2) 如何得到最优解递归式

a.分析原问题最优解和子问题最优解的关系；

例如矩阵连乘问题，我们假设已经知道在第k个矩阵加括号是最优的，即(AiAi+1…Ak)(Ak+1Ak+2…Aj)。作出最优选择后产生两个子问题：(AiAi+1…Ak)，(Ak+1Ak+2…Aj)。如果我们用m[i][j]表示AiAi+1…Aj矩阵连乘的最优解，那么两个子问题：(AiAi+1…Ak)，(Ak+1Ak+2…Aj)对应的最优解分别是m[i][k]，m[k+1][j]。剩下的只需要考察(AiAi+1…Ak)和(Ak+1Ak+2…Aj)的结果矩阵相乘的乘法次数了。两个结果矩阵相乘的乘法次数是pi*pk+1*qj。

因此，原问题最优解和子问题最优解的关系：m[i][j]= m[i][k]+m[k+1][j]+ pi*pk+1*qj

b.考察有多少种选择；

实质上，我们并不知道哪种选择是最优的，因此就需要考察有多少种选择，然后从这些选择中找到最优解。

例如矩阵连乘问题，加括号的位置k(AiAi+1…Ak)(Ak+1Ak+2…Aj)，k的取值范围是{i，i+1，…，j-1}，即i≤k<j，那么我们考察每一种选择，找到最优值。

c.得到最优解递归式。

例如矩阵连乘问题，m[i][j]表示AiAi+1…Aj矩阵连乘的最优解，根据最优解和子问题最优解的关系，并考察所有的选择，找到最小值就是我们要的最优解。