本章介绍频域,并使用 Python 示例介绍傅里叶级数、傅里叶变换、傅里叶属性、FFT、窗口和频谱图。
学习DSP和无线通信最酷的副作用之一是,您还将学会在频域中思考。大多数人在频域中工作的经验仅限于调整汽车音响系统上的低音/中/高音旋钮。大多数人在频域中观看某些内容的经验仅限于看到音频均衡器,例如以下剪辑:

在本章结束时,您将了解频域的真正含义,如何在时间和频率之间进行转换(以及当我们这样做时会发生什么),以及我们将在整个DSP和SDR研究中使用的一些有趣的原理。在本教科书结束时,您将保证成为频域工作的大师!
首先,为什么我们喜欢观察频域中的信号?这里有两个示例信号,分别在时域和频域中显示。
如您所见,在时域中,它们看起来都像噪声,但在频域中,我们可以看到不同的特征。一切都以很自然处于时域中;当我们对信号进行采样时,我们将在时域中对它们进行采样,因为您无法直接在频域中对信号进行采样。但有趣的事情通常发生在频域中。
傅里叶级数
频域的基础知识始于理解任何信号都可以由相加的正弦波表示。当我们将信号分解为复合正弦波时,我们称之为傅里叶级数。下面是仅由两个正弦波组成的信号示例:
另一个例子:下面的红色曲线通过对最多 10 个正弦波求和来近似锯齿波。我们可以看到,这不是一个完美的重建——由于急剧的过渡,需要无限数量的正弦波来重现这个锯齿波:
有些信号比其他信号需要更多的正弦波,有些信号需要无限量的正弦波,尽管它们总是可以用有限的数量近似。这是信号被分解为一系列正弦波的另一个示例:
要了解如何将信号分解为正弦波或正弦波,我们需要首先回顾正弦波的三个属性:
1.Amplitude 波幅
2.Frequency 频率
3.Phase相位
振幅表示波的“强度”,而频率是每秒的波数。相位用于表示正弦波如何在时间上偏移,从 0 到 360 度(或 0 到 2π ),但它必须相对于某物具有任何意义,例如两个具有相同频率的信号彼此异相 30 度。
在这一点上,您可能已经意识到“信号”本质上只是一个函数,通常表示为“随时间推移”(即x轴)。另一个容易记住的属性是周期,它是频率的倒数。正弦曲线的周期是波完成一个周期的时间量(以秒为单位)。因此,频率单位是 1/秒或 Hz。
当我们将信号分解为正弦波的总和时,每个正弦波都有一定的幅度、相位和频率。每个正弦波的振幅将告诉我们原始信号中存在的频率有多强。现在不要太担心相位,除了意识到sin()和cos()之间的唯一区别是相移(时间偏移)。
理解傅里叶级数的基本概念比实际方程更重要,但对于那些对这些方程感兴趣的人,我建议你参考 Wolfram 的简洁解释: https://mathworld.wolfram.com/FourierSeries.html 。
时频对(Time-Frequency Pairs)
我们已经确定信号可以表示为正弦波,正弦波具有多个属性。现在,让我们学习在频域中绘制信号。时域演示信号如何随时间变化,而频域显示信号在哪些频率中停留。x轴不是时间,而是频率。我们可以在时间和频率上绘制给定的信号。让我们看一些简单的例子开始。
以下是频率为f的正弦波在时域和频域中的样子:

时域应该看起来非常熟悉。这是一个振荡函数。不要担心它在周期的哪个点开始或持续多长时间。结论是信号具有单个频率,这就是为什么我们在频域中看到单个尖峰/峰值的原因。无论正弦波振荡的频率如何,我们都会看到频域中的尖峰。像这样的尖峰的数学名称称为“脉冲”。
现在,如果我们在时域中有一个脉冲呢?想象一下有人拍手或用锤子敲钉子的录音。这个时频对有点不那么直观。
如我们所见,时域中的脉冲在频域中是平坦的,理论上它包含每个频率。理论上没有完美的冲量,因为它在时域中必须是无限短的。就像正弦波一样,脉冲在时域中的哪个位置发生并不重要。这里重要的一点是,时域的快速变化会导致许多频率的发生。
接下来让我们看一下方波的时域和频域图:
这个也不太直观,但我们可以看到频域在 10 Hz 处有一个很强的尖峰,这是方波的频率,但它似乎也在继续。这是由于时域的快速变化,就像前面的例子一样。但它的频率并不平坦。它每隔一段时间就会出现峰值,并且水平会慢慢衰减(尽管它将永远持续下去)。时域中的方波在频域中具有sin(x)/x模式(也称为sinc函数)。
现在,如果我们在时域中有一个恒定的信号怎么办?恒定信号没有“频率”。 因为没有频率,所以在频域中,我们在 0 Hz 处有一个尖峰。仔细想想,这是有道理的。频域不会是“空的”,因为这只会在没有信号存在的情况下发生(即时域为0)。我们将频域中的 0 Hz 称为“DC”,因为它是由时间上的直流信号(不变的恒定信号)引起的。请注意,如果我们在时域中增加直流信号的幅度,则频域中0 Hz处的尖峰也会增加。
因为没有频率,所以在频域中,我们在 0 Hz 处有一个尖峰。仔细想想,这是有道理的。频域不会是“空的”,因为这只会在没有信号存在的情况下发生(即时域为0)。我们将频域中的 0 Hz 称为“DC”,因为它是由时间上的直流信号(不变的恒定信号)引起的。请注意,如果我们在时域中增加直流信号的幅度,则频域中0 Hz处的尖峰也会增加。
稍后我们将了解频域图中的y轴究竟意味着什么,现在您可以将其视为一种幅度,告诉您时域信号中存在多少频率。
傅里叶变换
在数学上,我们用来从时域到频域和返回的“变换”称为傅里叶变换。它的定义如下:

对于信号 x(t),我们可以使用此公式获得频域版本 X(f)。我们将用 x(t) 或 y(t) 表示函数的时域版本,用 X(f) 和 Y(f) 表示相应的频域版本。注意“t”表示时间,“f”表示频率。“j”只是虚数单位。你可能在高中数学课上看到过“我”。我们在工程和计算机科学中使用“j”,因为“i”通常是指当前,而在编程中,它通常用作迭代器。
从频率回到时域造作几乎相同,除了比例因子和负号:
请注意,许多教科书和其他资源使用 w 代替 2πf 。 w 是以弧度每秒为单位的角频率,而 f 是以 Hz 为单位。你所要知道的是

尽管它在许多方程中添加了一个 2 π 项,但更容易坚持以Hz为单位的频率。 最终,您将在SDR应用程序中使用Hz。
上述傅里叶变换方程是连续形式,您只会在数学问题中看到。离散形式更接近代码中实现的内容:

请注意,主要区别在于我们用求和替换了积分。索引 k 从 0 变为 N-1。
如果这些方程对你来说都没有多大意义,那也没关系。我们实际上不需要直接使用它们来做DSP和SDR的很酷的事情!
时频属性
上面我们研究了信号如何在时域和频域中出现的示例。现在,我们将介绍五个重要的“傅里叶性质”。这些属性告诉我们,如果我们对时域信号执行什么操作,那么相应就会发生在频域信号上。它将使我们深入了解我们将在实践中对时域信号执行的数字信号处理(DSP)类型。
1、线性特性:

2、 频移特性:

x(t) 左侧的术语是我们所说的“复正弦波”或“复指数”。现在,我们只需要知道它本质上只是一个频率  的正弦波。这个属性告诉我们,如果我们取一个信号 x(t) 并将其乘以正弦波,那么在频域中,我们得到的除了偏移某个频率
的正弦波。这个属性告诉我们,如果我们取一个信号 x(t) 并将其乘以正弦波,那么在频域中,我们得到的除了偏移某个频率  。这种频率的变化可能更容易可视化:
。这种频率的变化可能更容易可视化:
频移是DSP不可或缺的一部分,因为出于多种原因,我们希望在频率上上下移动信号。这个属性告诉我们如何做到这一点(乘以正弦波)。下面是可视化此属性的另一种方法:

3、按时间缩放属性

在等式的左侧,我们可以看到我们在时域中缩放信号x(t)。下面是一个信号按时间缩放的示例,然后每个信号的频域版本会发生什么。
按时间缩放实质上是收缩或扩展 x 轴上的信号。这个属性告诉我们的是,时域中的缩放会导致频域中的反向缩放。例如,当我们更快地传输比特时,我们必须使用更多的频率。该属性有助于解释为什么更高的数据速率信号占用更多的带宽/频谱。如果时间频率缩放是成比例的,而不是成反比的,蜂窝运营商将能够每秒传输他们想要的所有比特,而无需支付数十亿的频谱费用!不幸的是,事实并非如此。
已经熟悉此属性的人可能会注意到缺少比例因子;为了简单起见,它被省略了。出于实际目的,它没有区别。
4、在时域中卷积属性:
它被称为卷积属性,因为在时域中我们正在卷积 x(t) 和 y(t)。您可能还不知道卷积操作,所以现在将其想象为互相关。当我们卷积时域信号时,相当于将这两个信号的频域版本相乘。这与将两个信号相加非常不同。正如我们所看到的,当你添加两个信号时,实际上什么都没有发生,你只是将频域版本加在一起。但是当你卷积两个信号时,就像从它们创建一个新的第三个信号。卷积是DSP中最重要的技术,尽管我们必须首先了解滤波器的工作原理才能完全掌握它。
在我们继续之前,为了简要解释为什么这个属性如此重要,请考虑这种情况:你有一个想要接收的信号,旁边有一个干扰信号。
掩蔽的概念在编程中被大量使用,所以让我们在这里使用它。如果我们能创建下面的掩码,并将其乘以上面的信号以遮盖我们不想要的信号会怎样?
我们通常在时域中执行 DSP 操作,因此让我们利用卷积属性来了解如何在时域中进行这种掩码。假设 x(t) 是我们接收到的信号。设Y(f)是我们想要在频域中应用的掩码。这意味着y(t)是我们掩码的时域表示,如果我们用x(t)卷积它,我们可以“过滤掉”我们不想要的信号。
当我们讨论过滤时,卷积属性将更有意义。
5、在频域中卷积属性:
最后,我想指出卷积属性是反向工作的,尽管我们不会像时域卷积那样使用它:
还有其他属性,但在我看来,以上五个是最关键的。尽管我们没有逐步完成每个属性的证明,但关键是我们使用数学属性来深入了解当我们进行分析和处理时真实信号会发生什么。不要纠结于方程式。确保您了解每个属性的说明。
快速傅里叶变换 (FFT)
现在回到傅里叶变换。我向您展示了离散傅里叶变换的方程,但是您在编码时 99.9% 的时间将使用 FFT 函数 fft()。快速傅里叶变换 (FFT) 只是一种计算离散傅里叶变换的算法。它是几十年前开发的,尽管在实现上存在差异,但它仍然是计算离散傅里叶变换的统治者。幸运的是,考虑到他们在名称中使用了“快速”。
FFT 是一个具有一个输入和一个输出的函数。它将信号从时间转换为频率:

在本教教程中,我们将只处理一维FFT(2D用于图像处理和其他应用)。出于我们的目的,将 FFT 函数视为具有一个输入:一个样本向量;一个输出:该样本向量的频域版本。输出的大小始终与输入的大小相同。如果我将 1024 个样本输入 FFT,我将得到 1024 个样本。令人困惑的部分是,输出将始终在频域中,因此,如果我们要绘制x轴的“跨度”,它不会根据时域输入中的样本数量而改变。让我们通过查看输入和输出数组及其索引的单位来可视化它:
 由于输出在频域中,因此x轴的跨度基于采样率,我们将在下一章中介绍。当我们对输入向量使用更多样本时,我们在频域中获得了更好的分辨率(除了一次处理更多样本)。我们实际上并没有通过更大的输入来“看到”更多的频率。唯一的方法是增加采样率(减少采样周期
由于输出在频域中,因此x轴的跨度基于采样率,我们将在下一章中介绍。当我们对输入向量使用更多样本时,我们在频域中获得了更好的分辨率(除了一次处理更多样本)。我们实际上并没有通过更大的输入来“看到”更多的频率。唯一的方法是增加采样率(减少采样周期 t )。
t )。
我们如何实际绘制此输出?例如,假设我们的采样率为每秒 100 万个样本 (1 MHz)。正如我们将在下一章中学习的那样,这意味着无论我们输入FFT多少样本,我们只能看到高达0.5 MHz的信号。FFT 的输出表示方式如下: 情况总是如此;FFT 的输出将始终显示为
情况总是如此;FFT 的输出将始终显示为  ,其中
,其中  是采样率。即,输出将始终具有负部分和正部分。如果输入很复杂,则负部分和正部分将不同,但如果输入为实,则它们将是相同的。
是采样率。即,输出将始终具有负部分和正部分。如果输入很复杂,则负部分和正部分将不同,但如果输入为实,则它们将是相同的。
关于频率间隔,每个箱对应于Hz,即向每个FFT输入更多样本将导致输出中更精细的分辨率。如果您是新手,可以忽略一个非常小的细节:从数学上讲,最后一个索引并不完全对应于  ,而是对于大型 N ,它将大约为
,而是对于大型 N ,它将大约为  。
。
负频率
负频率到底是什么?现在,只要知道它们与使用复数(虚数)有关——在发送/接收射频信号时,实际上并没有“负频率”这样的东西,它只是我们使用的一种表示。这是一种直观的思考方式。考虑我们告诉SDR调整到100 MHz(FM无线电频段)并以10 MHz的速率采样。换句话说,我们将查看从 95 MHz 到 105 MHz 的频谱。也许存在三个信号:
现在,当 SDR 向我们提供样本时,它将如下所示:
请记住,我们将 SDR 调谐为 100 MHz。因此,当我们以数字方式表示时,大约97.5 MHz的信号显示为-2.5 MHz,从技术上讲,这是一个负频率。实际上,它只是低于中心频率的频率。当我们更多地了解抽样并获得使用我们的特别提款权的经验时,这将更有意义。
时域顺序不在重要(Order in Time Doesn’t Matter)
在我们进入FFT之前,最后一个属性。FFT函数有点“混合”输入信号以形成输出,该输出具有不同的比例和单位。毕竟,我们不再处于时域中。内化差异的一个好方法是认识到改变时域中事物发生的顺序不会改变信号中的频率分量。即,以下两个信号的FFT将具有相同的两个尖峰,因为信号只是不同频率的两个正弦波。改变正弦波的发生顺序并不会改变它们是不同频率的两个正弦波的事实。
从技术上讲,FFT值的相位会因为正弦曲线的时移而改变。然而,在本教程的前几章中,我们将主要关注FFT的规模。
Python 中的 FFT
现在我们已经了解了FFT是什么以及如何表示输出,让我们实际看一些Python代码并使用Numpy的FFT函数np.fft.fft()。
首先,我们需要在时域中创建一个信号。请随意使用您自己的 Python 控制台进行操作。为了简单起见,我们将在 0.15 Hz 下制作一个简单的正弦波。我们还将使用 1 Hz 的采样率,这意味着我们在 0、1、2、3 秒等时间采样。
import numpy as np
t = np.arange(100)
s = np.sin(0.15*2*np.pi*t)
如果我们绘制 s ,它看起来像:
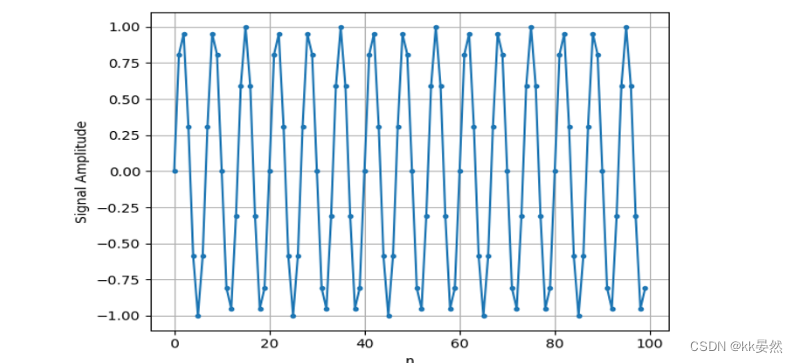
接下来让我们使用 Numpy 的 FFT 函数:
S = np.fft.fft(s)
如果我们查看 S ,我们会发现它是一个复数数组:
S = array([-0.01865008 +0.00000000e+00j, -0.01171553 -2.79073782e-01j,0.02526446 -8.82681208e-01j, ,…
提示:无论你在做什么,如果你遇到复数,试着计算幅度和相位,看看它们是否更有意义。让我们这样做,并绘制幅度和相位。在大多数语言中,abs() 是复数大小的函数。相位的函数各不相同,但在 Python 中它是 np.angle() 。
import matplotlib.pyplot as plt
S_mag = np.abs(S)
S_phase = np.angle(S)
plt.plot(t,S_mag,'.-')
plt.plot(t,S_phase,'.-')

现在我们没有为绘图提供任何 x 轴,它只是数组的索引(从 0 开始计数)。由于数学原因,FFT的输出具有以下格式:

但是我们希望中心为0 Hz(DC),左侧为负频率(这正是我们喜欢可视化事物的方式)。因此,每当我们进行FFT时,我们都需要执行“FFT移位”,这只是一个简单的阵列重排操作,有点像圆形移位,但更像是“把这个放在那里,放在那里”。下图完全定义了FFT移位操作的作用: 为了我们的方便,Numpy 有一个 FFT 移位函数, np.fft.fftshift() .将 np.fft.fft() 行替换为:
为了我们的方便,Numpy 有一个 FFT 移位函数, np.fft.fftshift() .将 np.fft.fft() 行替换为:
S = np.fft.fftshift(np.fft.fft(s))
我们还需要计算出 x 轴值/标签。回想一下,我们使用 1 Hz 的采样率来简化操作。这意味着频域图的左边缘将为-0.5 Hz,右边缘将为0.5 Hz。如果这没有意义,它会在您完成有关 IQ采样 的章节之后。让我们坚持采样率为1 Hz的假设,并使用适当的x轴标签绘制FFT输出的幅度和相位。下面是这个 Python 示例和输出的最终版本:
import numpy as np
import matplotlib.pyplot as plt
Fs = 1 # Hz
N = 100 # number of points to simulate, and our FFT size
t = np.arange(N) # because our sample rate is 1 Hz
s = np.sin(0.15*2*np.pi*t)
S = np.fft.fftshift(np.fft.fft(s))
S_mag = np.abs(S)
S_phase = np.angle(S)
f = np.arange(Fs/-2, Fs/2, Fs/N)
plt.figure(0)
plt.plot(f, S_mag,'.-')
plt.figure(1)
plt.plot(f, S_phase,'.-')
plt.show()

请注意,我们看到峰值为0.15 Hz,这是我们在创建正弦波时使用的频率。所以这意味着我们的FFT工作了!如果我们不知道用于生成正弦波的代码,但只是给了样本列表,我们可以使用 FFT 来确定频率。我们之所以在-0.15 Hz处看到尖峰,这与它是一个真实的信号有关,而不是复杂的,我们稍后会更深入地介绍。
窗口化
当我们使用FFT来测量信号的频率分量时,FFT假设它被赋予了一段周期性信号。它的行为就好像我们提供的信号继续无限期地重复一样。就好像切片的最后一个样本连接回第一个样本一样。它源于傅里叶变换背后的理论。这意味着我们希望避免第一个样本和最后一个样本之间的突然跃迁,因为时域中的突然跃迁看起来像许多频率,而实际上我们的最后一个样本实际上并没有连接回我们的第一个样本。简单地说:如果我们做一个 100 个样本的 FFT,使用 np.fft.fft(x) ,我们希望 x[0] 和 x[99] 的值相等或接近。
我们弥补这种循环属性的方式是通过“窗口化”。在FFT之前,我们将信号切片乘以窗口函数,该函数只是两端逐渐变细为零的任何函数。这可确保信号切片从零开始和结束并连接。常见的窗口函数包括汉明、汉宁、布莱克曼和凯撒(Hamming, Hanning, Blackman, and Kaiser)。当您不应用任何窗口化时,它被称为使用“矩形”窗口,因为它就像乘以数组一样。下面是几个窗口函数的样子
对于初学者来说,一个简单的方法是坚持使用汉明窗口,该窗口可以在 Python 中使用 np.hamming(N) 创建,其中 N 是数组中的元素数量,即您的 FFT 大小。在上面的练习中,我们将在 FFT 之前应用窗口。在第二行代码之后,我们将插入:
s = s * np.hamming(100)
如果你害怕选择错误的窗口,不要担心。与不使用窗户相比,汉明、汉宁、布莱克曼和凯撒之间的差异非常小,因为它们的两侧都逐渐变细并解决了根本问题。
FFT大小
最后要注意的是FFT大小。由于 FFT 的实现方式,最佳 FFT 大小始终为 2 量级(2的次方形式)。您可以使用不是 2 量级的大小,但速度会更慢。常见的尺寸在 128 到 4096 之间,尽管您当然可以更大。在实践中,我们可能不得不处理数百万或数十亿个样本长的信号,因此我们需要分解信号并执行许多FFT。这意味着我们将获得许多输出。我们可以将它们平均起来,也可以随着时间的推移绘制它们(特别是当我们的信号随时间变化时)。您不必将信号的每个样本都通过FFT来获得该信号的良好频域表示。例如,您只能在信号中每 100k 个样本中对 1024 个样本进行 FFT,只要信号始终打开,它仍然可能看起来不错。
频谱图/瀑布图
频谱图是显示频率随时间变化的图。它只是一堆堆叠在一起的FFT(垂直,如果你想在水平轴上的频率)。我们也可以实时显示它,通常称为瀑布。频谱分析仪是显示此频谱图/瀑布图的设备。下面是一个频谱图示例,频率在水平/x 轴上,时间在垂直/y 轴上。蓝色代表最低能量,红色代表最高能量。我们可以看到,中心有一个强烈的DC(0 Hz)尖峰,周围信号变化。蓝色代表我们的本底噪声

作为练习,尝试编写生成频谱图所需的 Python 代码。请记住,它只是堆叠在一起的FFT行,每行是1个FFT。确保在FFT大小的切片中对输入信号进行时间切片(例如,每个切片1024个样本)。为了简单起见,您可以输入一个真实信号,并在绘制频谱图之前简单地丢弃负一半的频率。下面是您可以使用的示例信号,它只是白噪声中的音调:
import numpy as np
import matplotlib.pyplot as plt
sample_rate = 1e6
# Generate tone plus noise
t = np.arange(1024*1000)/sample_rate # time vector
f = 50e3 # freq of tone
x = np.sin(2*np.pi*f*t) + 0.2*np.random.randn(len(t))
下面是它在时域中的样子(前 200 个样本):
频谱图代码示例(尝试先自己编写!
# simulate the signal above, or use your own signal
fft_size = 1024
num_rows = int(np.floor(len(x)/fft_size))
spectrogram = np.zeros((num_rows, fft_size))
for i in range(num_rows):
spectrogram[i,:] = 10*np.log10(np.abs(np.fft.fftshift(np.fft.fft(x[i*fft_size:(i+1)*fft_size])))**2)
spectrogram = spectrogram[:,fft_size//2:] # get rid of negative freqs because we simulated a real signal
plt.imshow(spectrogram, aspect='auto', extent = [0, sample_rate/2/1e6, 0, len(x)/sample_rate])
plt.xlabel("Frequency [MHz]")
plt.ylabel("Time [s]")
plt.show()
这应该产生以下内容,这不是最有趣的频谱图,因为没有时变行为。作为额外的练习,尝试添加时变行为,例如,看看你是否可以让音调开始和停止。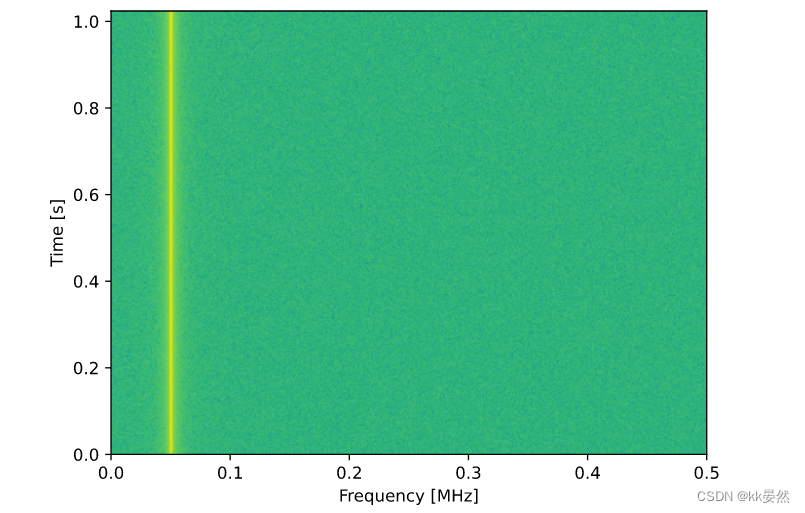








 本文介绍了频域的基础知识,包括傅里叶级数、傅里叶变换和FFT。通过Python示例,阐述了如何将信号从时域转换到频域,探讨了傅里叶变换的属性,如线性、频移、时间缩放、卷积等。还讨论了窗口化在处理信号时的重要性,以及FFT大小的选择。最后,简述了频谱图的生成和其在信号分析中的应用。
本文介绍了频域的基础知识,包括傅里叶级数、傅里叶变换和FFT。通过Python示例,阐述了如何将信号从时域转换到频域,探讨了傅里叶变换的属性,如线性、频移、时间缩放、卷积等。还讨论了窗口化在处理信号时的重要性,以及FFT大小的选择。最后,简述了频谱图的生成和其在信号分析中的应用。
















 3923
3923

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








