Pipage Rounding 学习笔记

Pipage Rounding 学习笔记

Author: Sijin Yu

本文基本只作简单的翻译工作. 未经作者授权不得转载.

1. Linear Programming (线性规划)

线性规划可以表示为

$$\begin{array}{rl}\min & c\cdot x\\ \text{subject to }& Ax\ge b\end{array}$$

其中, $n$ 为变量个数 ($x$ 的维度), $m$ 为非平凡约束的个数.
则:

• $A$ 有 $(m+n)$ 行和 $n$ 列, 且 $\text{rank}(A)=n$.
• 令 $Bx=b_B$, 其中 $\text{rank}(B)=n$, $B$ 是 $A$ 的子阵, $b_B$ 是 $b$ 中对应的元素.

1.1 基本定义

$$\begin{array}{rl}\min & c\cdot x\\ \text{subject to }& Ax\ge b\end{array}$$

• 基: $A$ 中 $n$ 列向量组成的线性无关的可逆矩阵 (就是 $B$).

• 基向量: 基 $B$ 中任意一个列向量.

• 基本解: $Bx=b_B$ 的解.

• 可行解: 在多面体 $Ax\ge b$ 中的解.

• 基本可行解: 同时是基本解和可行解的解.

1.2 基本定理

• 对每个 LP 问题, 都存在一个最优解是基本可行解.

设 $x$ 为一个基本可行解, 令 supp ( x ) : = { i : x i > 0 } \text{supp}(x):=\{i:x_i>0\} supp(x):={ i:xi​>0}.

• 对每个 LP 问题, 都存在一个最优解, 使至少 $\text{supp}(x)$ 个线性无关的的非平凡约束取等号.

定理: 对于一个凸集 $k$ 与凸集外一点 $x$, 总存在超平面使得 $k$ 与 $x$ 分居两侧.

Separation Oracle: 给定一个点 $x$, 其关于凸集合 $k$ 的 separation oracle 为: 要么说明 $x\in k$, 要么返回一个分割 $x$ 与 $k$ 的超平面.

• 如果 $m=\text{ploy(n)}$, 则存在多项式时间的 Separation Oracle 算法.

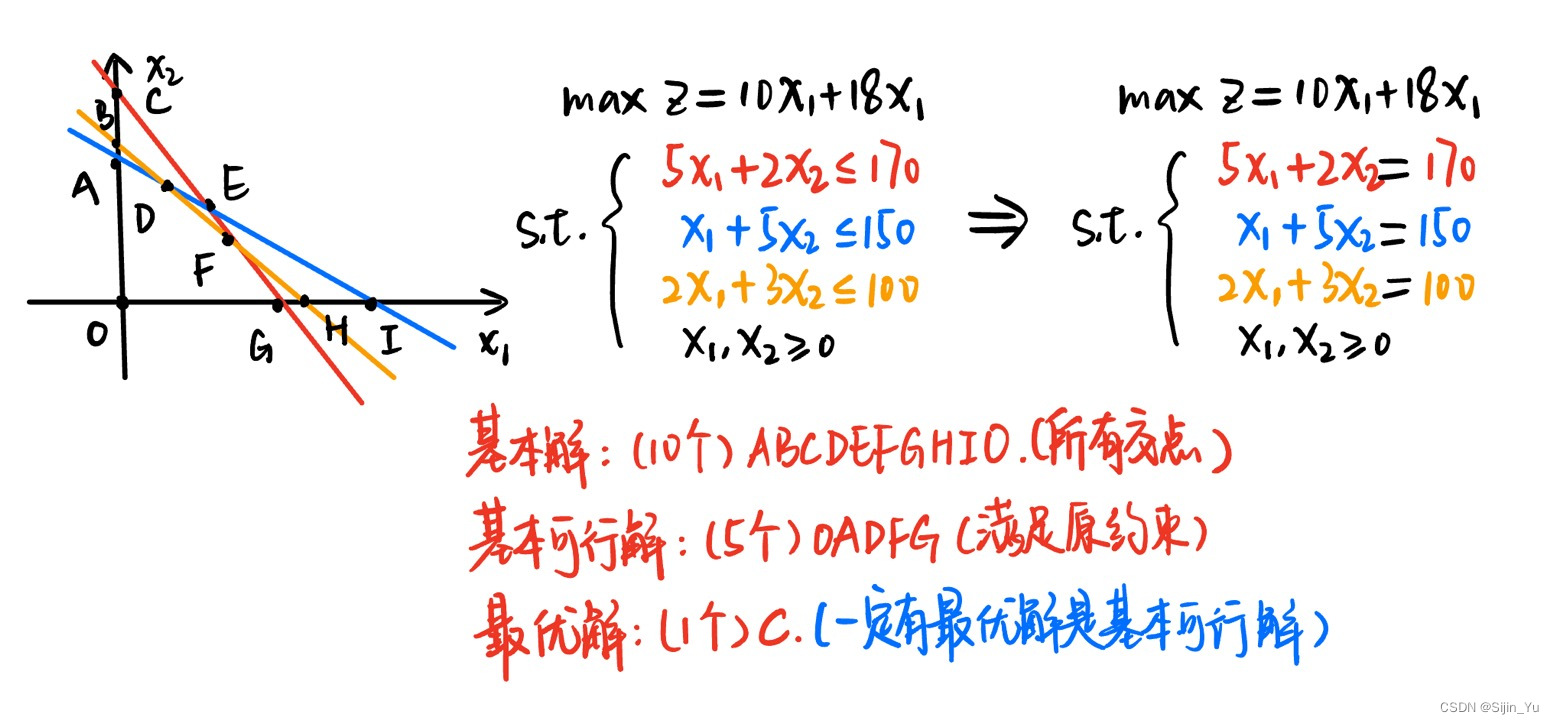
该图直观解释了: 总存在一个最优解是基本可行解.

1.3 椭球算法

椭球算法是一个在多项式时间内解决线性规划问题的算法.

算法步骤:

Step 1 猜想一个可能的 $M$, 判断 $c\cdot x\le M$ 和约束 $Ax\ge b$ 是否满足.

• 若满足: 降低 $M$ 值, 重新执行 Step 1.
• 若不满足: 得到分割超平面, 并提高 $M$ 至超平面另一侧.

经过有限次迭代, $M$ 趋于取最优解时 $c\cdot x$ 的值.

Step 1 的判断本质上是将 $c\cdot x\le M$ 放入约束中, 并针对 $x$ 和新约束对应的多面体执行 Separation Oracle 算法.

总结 of 1. Linear Programming (线性规划)

• 线性规划为: 在一个超多面体内寻找一个点, 使一个线性的函数取得最小值.
• 总存在一个最优解, 是基本可行解.
• 一个最优的基本可行解可在多项式时间内被找到.

---

2. Pipage Rounding

背景:

当线性规划的解只能取整数解时, 即原 LP 问题变为:
$$\begin{array}{rl}\min & c\cdot x\\ \text{subject to }& Ax\ge b\\ & x_j\in \mathbb{N},\forall j\in [n]\end{array}$$
则, 从线性规划变为整数规划, 问题从多项式变为 NP-hard.

2.1 Linear Relaxations (线性松弛)

现在考虑 0-1 规划问题, 即 x j ∈ { 0 , 1 } , ∀ j ∈ [ n ] x_j \in \{0,1\}, \forall j\in[n] xj​∈{ 0,1},∀j∈[n].

线性松弛: 将整数约束 x j ∈ { 0 , 1 } x_j \in \{0,1\} xj​∈{ 0,1} 用分数约束 $0\le x_j\le 1$ 替代, 在多项式时间内可解得分数约束下的最优解. 然后使用 pipage rounding 将分数下的最优解 “round” 到整数下, 可以证明这样的解是一个近似最优.

2.2 Pipage Rounding

记 $\mathcal{P}$ 为一 $n$ 维多面体. 一个 0-1 规划问题为:
max ⁡ { F ( x ) :     x ∈ P ∩ { 0 , 1 } n } \max\{F(x): ~~~x\in\mathcal{P}\cap\{0,1\}^n\} max{ F(x):   x∈P∩{ 0,1}n}
其中, $F(x)$ 为目标函数, $\mathcal{P}$ 为约束条件.

假设:

1. 对所有非整数的 $x\in \mathcal{P}$, 总是存在一个向量 $v_x$ 与两个标量 ${\alpha }_x,{\beta }_x>0$, 使得:
   $x+{\alpha }_x{v}_x$ 与 $x-{\beta }_x{v}_x$ 比起 $x$ 都有严格更大数量的整数坐标.
2. $F(x)$ 在 $v_x$ 方向上是凸函数.

则, 存在 pipage rounding 的方法,使: 给定任意的分数向量 $x\in \mathcal{P}$, 总能找到整数向量 $x^{\text{int}}\in \mathcal{P}$, 使得 $F(x^{\text{int}})\ge F(x)$ 成立.

Pipage Rounding 的一个例子

• 记 P : = { x ∈ [ 0 , 1 ] n : ∑ j = 1 n x j = k } \mathcal P:=\{x\in[0,1]^n: \sum_{j=1}^n x_j=k\} P:={ x∈[0,1]n:∑