Codeforces Round #724 (Div. 2) （A~D）题解

传送门
题目大意：
有n个数字，可以添加m个数字，使得n+m个数字两两之间差值的绝对值都存在在当前的数组中。

思路：
首先，如果数组中有负数。例如：-5,3对于这两个数字来说，|3-（-5）| = 8，会不断衍生更大的数字，无法满足条件。
其次，通过枚举情况，我们发现所有数字之间满足是非零最小数的所有整数倍。

代码：

#include<bits/stdc++.h>
using namespace std;

#define debug(a) cout << #a << ": " << a << endl;
#define LL long long 
#define IO ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)

void solve()
{
    int n;
    cin >> n;
    bool si = true,s0 = false;
    int x,ans,ma = 0;
    cin >> x;
    ans = x;
    ma = max(ma,x);
    if(x < 0) si = false;
    else if(x == 0) s0 = true;
    for(int i = 1;i < n;++i) {
        cin >> x;
        if(x < 0) si = false;
        else if(x == 0) s0 = true;
        ans = __gcd(x,ans);
        ma = max(ma,x);
    }
    int cnt = 0;
    if(s0) cnt++;
    cnt += (ma / ans);
    if(cnt <= 300 && si) {
        cout << "YES" << endl << cnt << endl;
        int m = ans;
        if(s0) cout << 0 << ' ';
        while(ma != ans) {
            cout << ans << ' ';
            ans += m;
        }
        cout << ma << endl;
    }
    else {
        cout << "NO" << endl;
    }
}

int main()
{
    IO;
    int t;
    cin >> t;
    while(t--){
        solve();
    }
    return 0;
}

总结：
数字的性质，需要有一定的打表和数字感觉。

传送门
题目大意：
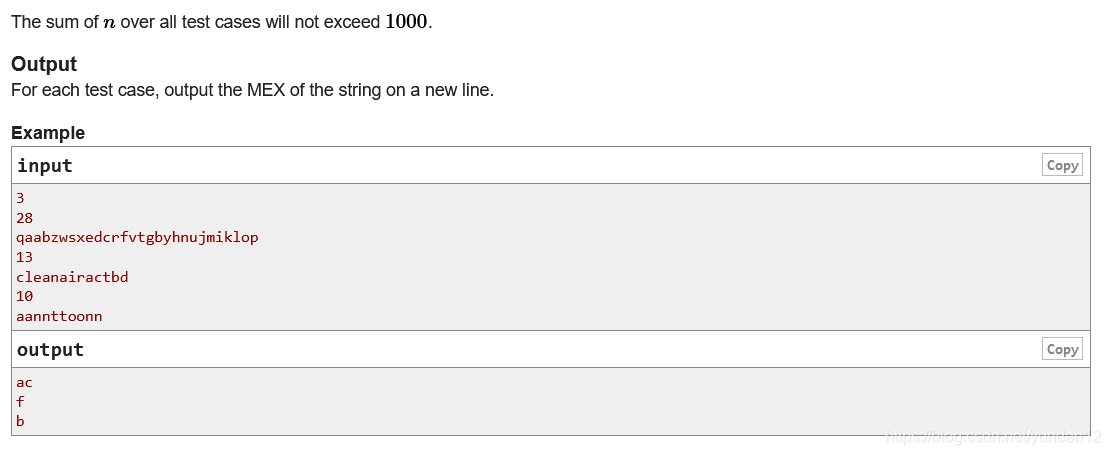
求未出现的最小的字典序的字符串

思路：
由于数据量范围较小，可以将每一个出现的字符串记录下来，从最小序枚举未出现的字符串

代码：

#include<bits/stdc++.h>
using namespace std;

#define debug(a) cout << #a << ": " << a << endl;
#define LL long long 
#define IO ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)

int a[30];
int b[30][30];
int c[30][30][30];

void solve()
{
    memset(a,0,sizeof(a));
    memset(b,0,sizeof(b));
    memset(c,0,sizeof(c));
    int n;
    cin >> n;
    string s;
    cin >> s;
    for(int i = 0;i < n;++i) {
        a[s[i]-'a'] = 1;
        if(i < n-1) b[s[i]-'a'][s[i+1]-'a'] = 1;
        if(i < n-2) c[s[i]-'a'][s[i+1]-'a'][s[i+2]-'a'] = 1;
    }
    //cout << 1 << endl;
    for(int i = 0;i < 26;++i) {
        if(a[i] == 0) {
            cout << char(i+'a') << endl;
            return ;
        }
    }
    for(int i = 0;i < 26;++i) {
        for(int j = 0;j < 26;++j) {
            if(b[i][j] == 0) {
                cout << char(i+'a') << char(j+'a') << endl;
                return ;
            }
        }
    }
    for(int i = 0;i < 26;++i) {
        for(int j = 0;j < 26;++j) {
            for(int k = 0;k <26;++k) {
                if(c[i][j][k] == 0) {
                    cout << char(i+'a') << char(j+'a') << char(k+'a') << endl;
                    return ;
                }
            }
        }
    }
}

int main()
{
    int t;
    cin >> t;
    while(t--){
        solve();
    }
    return 0;
}

总结：
数据量较小时，枚举的做法正确率高，但是代码量大

传送门

题目大意：
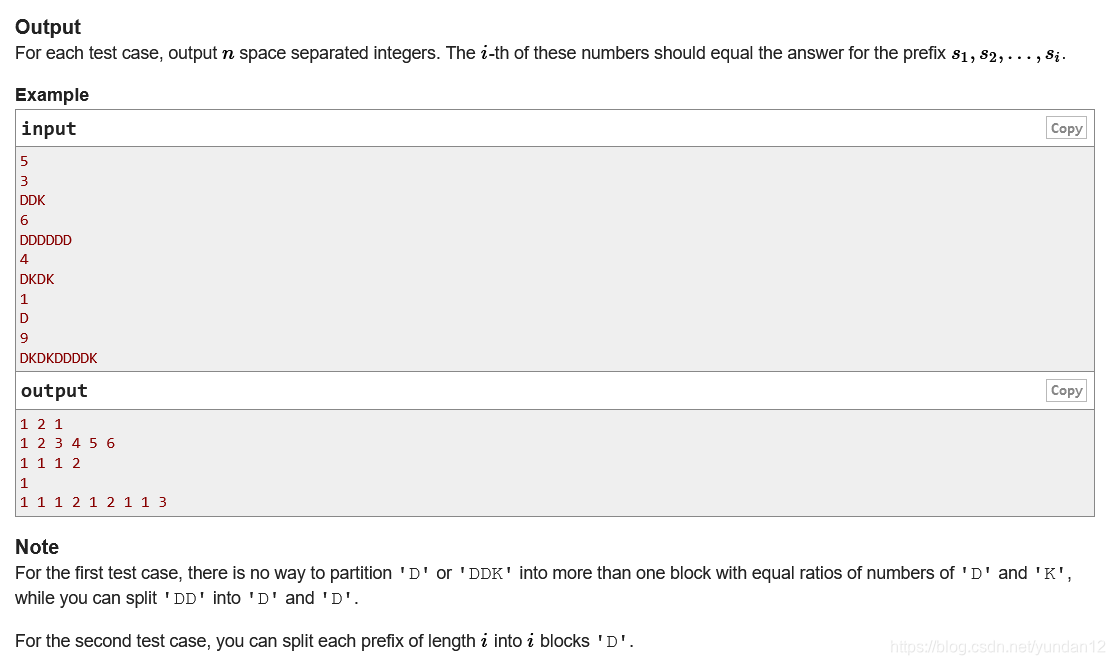
将字符串可以分割为最多多少个比例相同的子串，分割后所有子串必须比例相同。

思路：
每次将当前比例的个数加1，例如：如果之前有1:2的比例，对于2：4的样例就可以拆成两个1:2的样例。依次类推，除以最大公因数的比例所求出的个数就是最大个数。

代码：

#include<bits/stdc++.h>
using namespace std;

map<pair<int,int>,int> cnt;
void solve()
{
    cnt.clear();
    int n;
    cin >> n;
    string s;
    cin >> s;
    int l = 0,r = 0;
    for(int i = 0;i < n;++i) {
        if(s[i] == 'D') l++;
        else r++;
        int t = __gcd(l,r);
        cnt[{l/t,r/t}]++;
        cout << cnt[{l/t,r/t}] << ' ';
    }
    cout << endl;
}

int main()
{
    int t;
    cin >> t;
    while(t--) {
        solve();
    } 
    return 0;
}

总结：
数字比例的性质，记作拆分性。

传送门

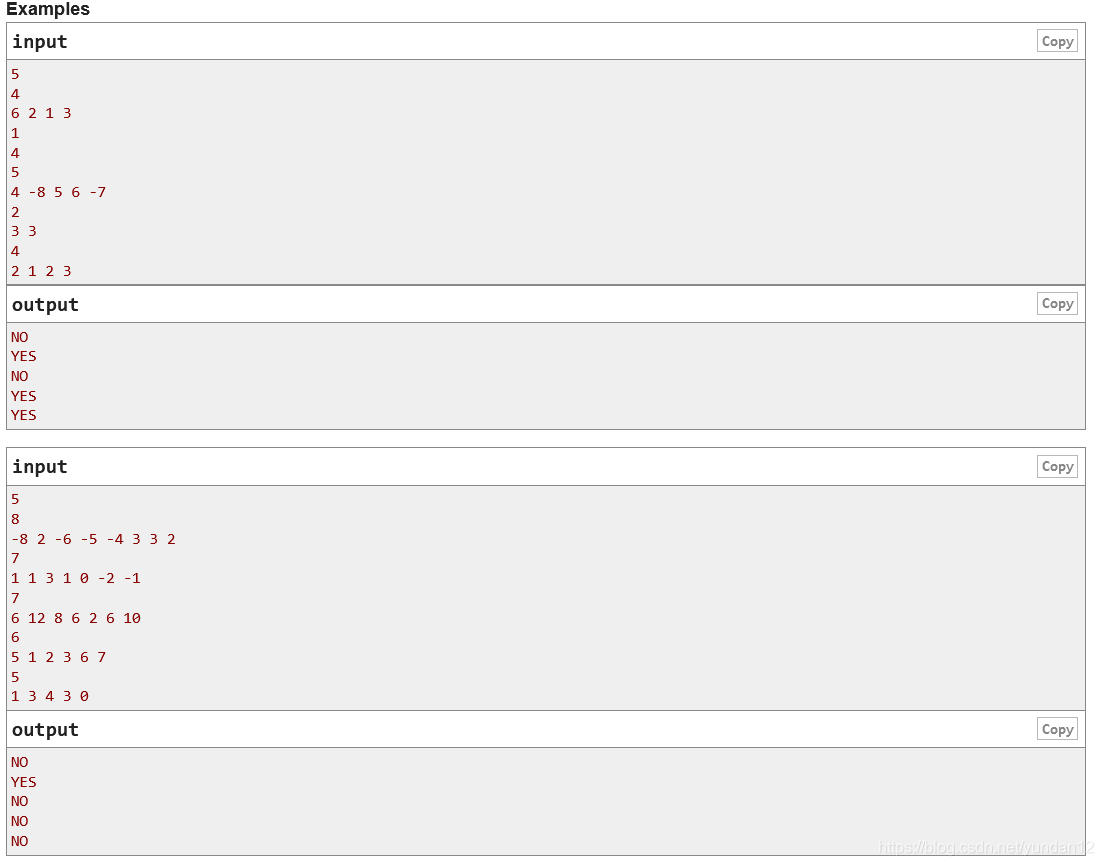
题目大意：
给定一个b序列，是否存在一个a序列满足a1,a2,…,a2i-1满足a1到a2i-1的中位数为bi

思路：
假定a序列刚开始为空，a1 = b1,那么对于下一个bj来讲,bj在a序列中一定要紧邻bj-1，中位数性质。

代码：

#include<bits/stdc++.h>
using namespace std;

#define debug(a) cout << #a << ": " << a << endl;
#define LL long long 
#define IO ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)

const int maxn = 2e5+10;
int a[maxn];
set<int> s;

void solve()
{
    int n;
    cin >> n;
    for(int i = 0;i < n;++i) {
        cin >> a[i];
    }
    s.clear();
    s.insert(a[0]);
    bool si = true;
    for(int i = 1;i < n;++i) {
        int pre = a[i-1];
        if(pre != a[i]) {
            if(pre < a[i]) {
                auto it = s.upper_bound(pre);
                if((it != s.end()) && (*it < a[i])) {
                    si = false;
                    break;
                }
            }
            else {
                auto it = s.lower_bound(pre);
                if((it != s.begin()) && (*(--it) > a[i])) {
                    si = false;
                    break;
                }
            }
        }
        s.insert(a[i]);
    }
    if(si) cout << "YES" << endl;
    else cout << "NO" << endl;
}

int main()
{
    IO;
    int t;
    cin >> t;
    while(t--){
        solve();
    }
    return 0;
}

总结：
中位数的性质，具有强烈的数学渲染感。