谓词逻辑——离散数学part 2

谓词

命题中把描述个体词的特性或关系部分称为谓词。如果含有n个个体词，则称为为n元谓词。一般地，一元谓词表达了个体词的性质，多元谓词表达了个体词之间的关系。
显然谓词不是命题，只有填入个体词后才能成为命题，所以把已经确定真值的命题看作0元谓词。
命题函数：eg A(x)：x是人。 B(x,y):x+y=1。
谓词的函数表示形式。简单命题函数的定义域为所有个体词的集合，即个体域的论述范围，也称为个体域，值域为命题的集合。
简单命题函数经过联结词运算后构成复合命题函数称为命题函数。
注意：不说明个体域就指全总个体域，相当于全宇宙。

量词

全称量词

$\forall x$，表示“所有的x”，“每一个x”，“凡是x”，“任意的x”
已知命题函数不是命题，但在$\forall x$的作用下，仅含变量x的命题函数为命题，有真值，全称量词约束了x的变量作用。
注意：当个体域采用全总个体域时，必须使用特性谓词，且在全称量词的作用下，特性谓词和命题函数之家必须采用蕴含联结词而不能用合取。
eg “所有狼都是犬科动物”，W(x):x是狼 D(x): x是犬科动物 当个体域不是狼而是全总个体域时，命题表示为 $(\forall x)(W(x)\to D(x))$

存在量词

$\exists x$,表示存在着x，有些x。
与全称量词一样，一个含有变量x的命题函数在存在量词的作用下，x不在起变量的作用，即存在量词约束了x的变量作用。
注意：当个体域采用全总个体域时，必须使用特性谓词，且在存在量词的作用下，特性谓词和命题函数之家必须采用合取联结词

消除量词

注意多个量词时消除的先后顺序

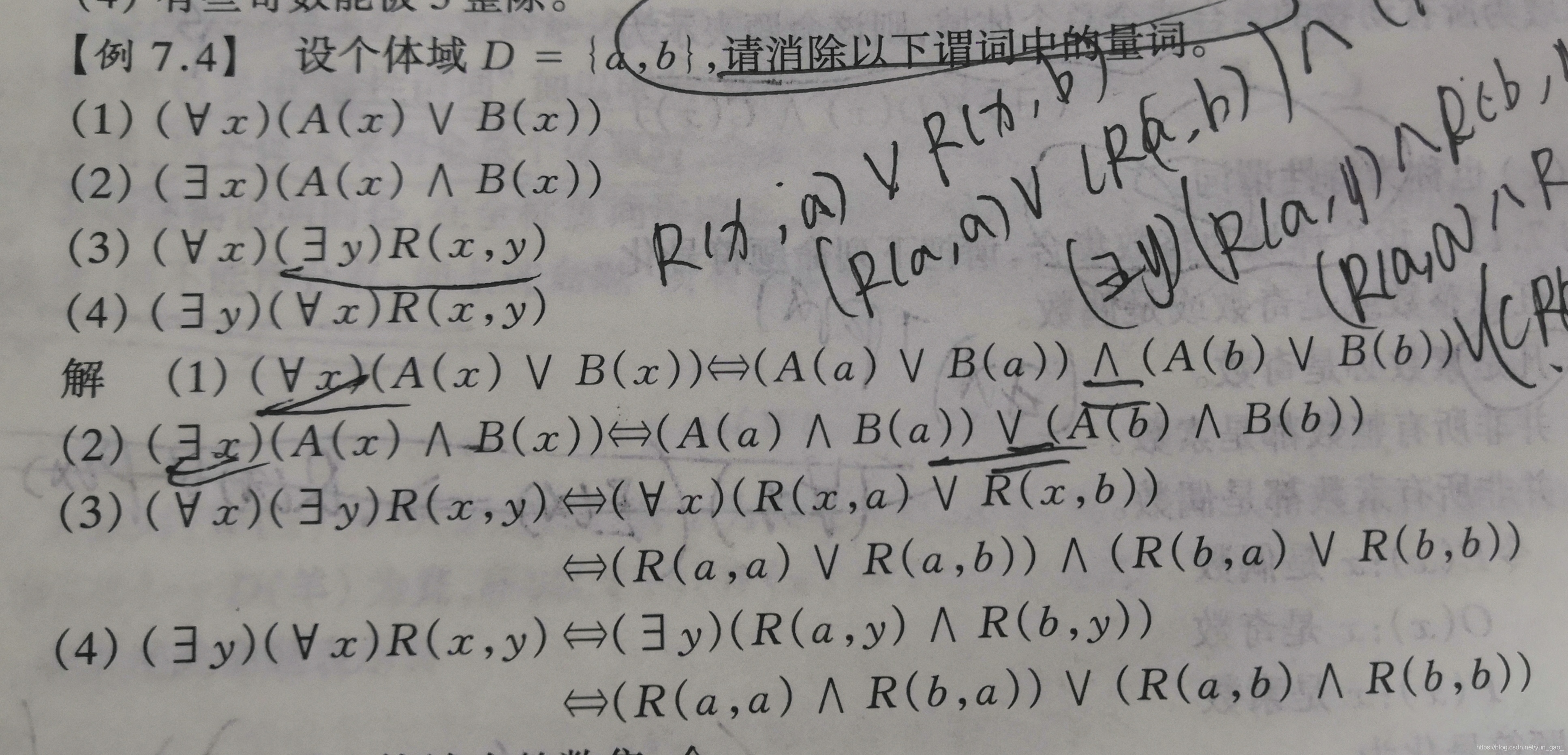
注意：量词顺序
eg
$\forall x\exists yP(x,y)$ :对任意的x，存在y使得满足P(x,y)
$\exists xforall$