插入排序

最新推荐文章于 2022-09-18 08:08:24 发布

心猿意碼

最新推荐文章于 2022-09-18 08:08:24 发布

阅读量8.6k

点赞数

CC 4.0 BY-SA版权

分类专栏：数据结构和算法文章标签：排序算法算法

本文链接：https://blog.youkuaiyun.com/yucaixiang/article/details/105788608

数据结构和算法专栏收录该内容

14 篇文章

订阅专栏

本文深入解析了插入排序算法的基本思想及其实现过程，通过逐步演示如何将无序元素插入已排序序列，展示了算法的工作原理。文章详细解释了算法的时间复杂度，包括最好、最坏和平均情况下的性能分析。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

插入排序（Insertion Sorting）的基本思想：

把 n个待排序的元素看成为一个有序表和一个无序表，开始时有序表中只包含一个元素，无序表中包含有 n-1个元素，排序过程中每次从无序表中取出第一个元素，把它的排序码依次与有序表元素的排序码进行比较，将它插入到有序表中的适当位置，使之成为新的有序表。

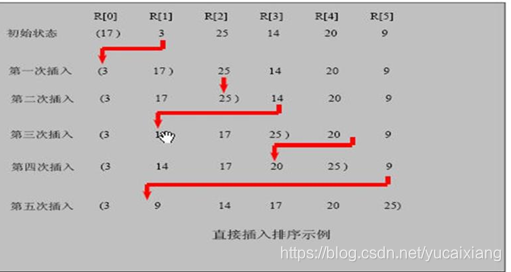
插入排序思路图：

括号内为有序表

代码实现：

package com.atguigu;
import java.util.Arrays;


public class InsertSort {

	public static void main(String[] args) {
		int[] arr = {101, 34, 119, 1, -1, 89};
		insertSort(arr); //调用插入排序算法
		System.out.println(Arrays.toString(arr));
	}

	//插入排序
	public static void insertSort(int[] arr) {
		int insertVal = 0;
		int insertIndex = 0;
		//使用for循环来把代码简化
		for(int i = 1; i < arr.length; i++) {
			//定义待插入的数
			insertVal = arr[i];
			insertIndex = i - 1; // 即arr[1]的前面这个数的下标

			// 给insertVal 找到插入的位置
			// 说明
			// 1. insertIndex >= 0 保证在给insertVal 找插入位置，不越界
			// 2. insertVal < arr[insertIndex] 待插入的数，还没有找到插入位置
			// 3. 就需要将 arr[insertIndex] 后移
			while (insertIndex >= 0 && insertVal < arr[insertIndex]) {
				arr[insertIndex + 1] = arr[insertIndex];// arr[insertIndex]
				insertIndex--;
			}
			// 当退出while循环时，说明插入的位置找到, insertIndex + 1
			//这里我们判断是否需要赋值
			if(insertIndex + 1 != i) {
				arr[insertIndex + 1] = insertVal;
			}

		}

	}

}

最坏时间复杂度—Θ(n2)
如果数组是倒序的，每次插入就相当于在数组的第一个位置插入数据。比如将 0 插入到数组[2, 3, 5, 7, 11]中，因为数组中的元素都大于 0 ，所以
需要需要与数组中的所有元素进行比较并以此将元素向右移动，最终将0 插入到数组第一个位置。通常来讲，假设数组的length为n，将元素插入到数组的操作称为insert，被插入元素Key需要与数组元素进行比较的此时称为K。那么在这种情况下，将某一个元素插入到数组时 k = n - 1。
综上所述，在插入排序的流程中，第一次进行insert时K = 1，第二次K = 2，第三次K = 3…最后一次K = n - 1.因此插入排序所用的总的时间为：
1 + 2 + 3 + ⋯ (n−1) = (1+2+3+⋯+(n−1)) = n2 / 2 - n / 2 用big-Θ表示法表示就是 Θ(n2)

最好时间复杂度—Θ(n)
那么插入排序可以使用少于Θ(n2) 的时间吗？答案是肯定的。如果要排序的数据已经是有序的，我们并不需要搬移任何数据。从尾到头在有序数据组里查找插入位置每次只需要比较一个数据就能确定插入的位置，所以这种情况下，最好时间复杂度是Θ(n)

平均时间复杂度
试想一下，如果被插入数组的排序是随机的，那感觉概率学，平均情况下此数组中的每一个元素都会比其它一半的元素小。
基于这样的一个概念下，调用insert往数组中插入元素时就需要进行 K/2 次比较。同事插入排序会固定执行 N - 1 此insert操作，所以插入排序的平均时间复杂度也是 Θ(n2)