决策树实验报告

实验目的

（1）掌握决策树算法的相关概念及含义；
（2）掌握决策树算法求解问题的流程；
（3）能够编写出决策树算法（任选一个即可）求解某一问题的代码；
（4）能够分析实验结果，对算法进行评估。

实验内容

该实验内容包括以下三部分：

（1）需要对决策树算法中的CART算法的相关概念进行阐述；

（2）任选一个数据集（Sklearn自带数据集、自动生成数据集、爬虫得来的数据集、各大竞赛平台下载的数据集、来自实际生活的数据集均可）。

    需要阐述所选定的数据集（该数据集是关于什么的数据集，各个特征表达的含义，标签的含义等等）。

（3）设计实验方案，进行仿真和预测（主要包含：导包、导入数据集、特征和标签的提取、训练集和测试集的划分、特征处理（根据实际情况可选）、CART算法对象的创建、在训练集上进行学习、在测试集上进行预测）。

算法的描述，数据集的描述

CART算法的阐述：
1.分裂准则：
CART算法使用一种贪婪的递归分裂策略，通过选择最佳的特征和阈值来进行数据分裂。对于分类任务，通常使用基尼指数（Gini index）或信息增益（information gain）来评估特征的分裂效果；对于回归任务，通常使用平方误差（mean squared error）来评估分裂效果。
2.分裂过程：
在每个节点上，CART算法会尝试所有可能的特征和阈值的组合，选择能够最大程度地提高纯度（或者减小误差）的分裂方式。这个过程会一直持续，直到达到预先设定的停止条件，比如树的最大深度、节点中样本数量的最小值等。
3.剪枝策略：
CART算法在生成完全的决策树后，会进行剪枝以防止过拟合。剪枝的目标是通过调整树的复杂度来提高泛化能力。CART算法使用代价复杂度剪枝（cost complexity pruning），通过引入一个复杂度参数来平衡模型的复杂度和拟合能力，选择最优的子树。
4.多变量决策树：
CART算法可以处理多变量（多分类或多输出）的问题。对于分类任务，CART算法可以生成多变量决策树，每个节点可以有多个分支，对应不同的类别；对于回归任务，CART算法也可以生成多变量决策树，每个节点可以有多个分支，对应不同的输出值。
数据集的描述：
数据集来自于UCI 官网。https://archive.ics.uci.edu/dataset/2/adult 这是数据集的实际网址。
该数据集总共有15列，除去标签列，总共有14列。而且有几个非数值特征都有7个以上的域。我使用到的是成年人的收入数据集。
特征总共有年龄，工作类，fnlwgt，教育，教育年限，婚姻状况，职业，关系，比赛，性别，资本收益，资本损失，每周工作时间，原国籍，以及收入（k每年）。

这是一个二分类的问题，数据集中两个类别的比例是3比1。
因为特征数众多的缘故，所以我把我认为影响较小的fnlwgt，婚姻状况，关系，资本收益，资本损失这些特征删除了，因为原国籍种类太多，所以根据是否为发达国家进行了划分。根据受教育年限划分了初等，中等，高等。

实验详细操作步骤或程序清单

下边是对表格进行预处理的代码

import pandas as pd

# 读取CSV文件
data = pd.read_csv('../datas/adult.csv')  # 这个数据集总共有好几个文件，只用了这一个表格

# 添加列名
data.columns = ['age', 'workclass', 'fnlwgt', 'education', 'education-num', 'marital-status', 'occupation',
                'relationship', 'race', 'sex', 'capital-gain', 'capital-loss', 'hours-per-week', 'native-country',
                'income']

# 删除指定的列
data = data.drop(['education', 'marital-status', 'capital-gain', 'capital-loss'], axis=1)

# 定义发达国家列表
# developed_countries = ['United-States', 'Canada', 'England', 'Germany', 'Japan']
developed_countries = ['united-states', 'canada', 'england', 'germany', 'japan']

# 遍历每一行数据
for index, row in data.iterrows():
    country = row['native-country'].strip().lower()  # 清洗并转换为小写

    # 判断原国籍是否为发达国家
    if row['native-country'].strip().lower() in developed_countries:
        data.at[index, 'is_developed'] = 1
    elif row['native-country'].strip().lower() not in developed_countries:
        data.at[index, 'is_developed'] = 0

# 删除原国籍列
data = data.drop('native-country', axis=1)

# 保存结果到新的文件
data.to_csv('new_file.csv', index=False)

下边是正式的代码包括了plt的汉化，标准化或均一化的代码，补充默认值。等等。

import pandas as pd
from sklearn.tree import DecisionTreeClassifier, plot_tree
from sklearn.model_selection import train_test_split, cross_val_score
from sklearn.impute import SimpleImputer
from sklearn.preprocessing import StandardScaler, MinMaxScaler
import matplotlib.pyplot as plt
import numpy as np
from sklearn.metrics import precision_recall_curve, auc, roc_auc_score

# 导入必要的包库。

# 读取数据集
df = pd.read_csv('dealed.csv')

print(df)
print(df.head())

# 查看数据集的格式和头几个信息。

plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 对plt进行设置字体，使其可以显示微软雅黑中文字体

tr = ['年龄', '受教育年限', '每周工作小时数', '是否为发达国家',
      '工作类别_ ?', '工作类别_ 联邦政府', '工作类别_ 地方政府',
      '工作类别_ 从未工作', '工作类别_ 私人企业',
      '工作类别_ 自雇-有公司', '工作类别_ 自雇-无公司',
      '工作类别_ 州政府', '工作类别_ 无报酬',
      '种族_ 美洲印第安', '种族_ 太平洋岛民', '种族_ 黑人',
      '种族_ 其他', '种族_ 白人', '性别_ 女性', '性别_ 男性']
# 特征列表。

columns_to_impute = ['workclass', 'occupation', 'education-num']
# 需要处理的缺失值列表。

num_imputer = SimpleImputer(strategy='mean')
cat_imputer = SimpleImputer(strategy='most_frequent')

# 对数值型特征列按照最多的进行填充
df['education-num'] = num_imputer.fit_transform(df[['education-num']])

# 对非数值型特征列进行填充
df[['workclass', 'occupation']] = cat_imputer.fit_transform(df[['workclass', 'occupation']])

X = df[['age', 'workclass', 'education-num', 'race', 'sex', 'hours-per-week', 'is_developed']]
X = pd.get_dummies(X)  # 对非数值型的特征列进行独热编码
y = df['income']

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y)

# 将标签值转换为0和1
y_train_binary = y_train.map({' <=50K': 0, ' >50K': 1})
y_test_binary = y_test.map({' <=50K': 0, ' >50K': 1})

"""
# # 标准化
# scaler = StandardScaler()
# 标准化的准确率为：0.8108108108109
# 最后的哪个值为： 0.763146446533786
"""

# 均一化
scaler = MinMaxScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)
# '''
# 最大深度：最后的平均指标
# 4 :0.7848067157420652
# 5 :0.8170071262981381
# 6 :0.8244324662177864
# 7 :0.827031744846509
# 8 :0.8622778632995517
# 9 :0.8608320178052615
# 10:0.8866437122454337
# '''
# 初始化决策树分类器
dtc = DecisionTreeClassifier(max_depth=9, ccp_alpha=0.000207)
# 训练模型
dtc.fit(X_train, y_train)
accuracy = dtc.score(X_test, y_test)
print(f"模型在测试集上的准确率为: {accuracy}")

# 使用决策树模型对测试集进行预测并获取预测概率值
y_scores = dtc.predict_proba(X_test)[:, 1]
# 计算精确率和召回率
precision, recall, _ = precision_recall_curve(y_test_binary, y_scores)

# 因为该数据集的两个类别比为3:1。所以使用AUC来进行评价模型。
# 计算PR曲线下的面积
pr_auc = auc(recall, precision)

# 计算AUC
roc_auc = roc_auc_score(y_test_binary, y_scores)

# 可视化PR曲线
plt.plot(recall, precision, marker='.')
plt.xlabel('Recall')
plt.ylabel('Precision')
plt.title('Precision-Recall curve')
plt.show()

# 打印AUC指标
print('PR AUC:', pr_auc)
print('ROC AUC:', roc_auc)

# 使用 5 折交叉验证来评估模型
scores = cross_val_score(dtc, X, y, cv=5)
print(f"模型的准确率：{scores.mean()} +/- {scores.std()}")

# 可视化决策树，但是只有上边的参数才能够勉强能够看清文字。所以损失了不少的准确性。
plt.figure(figsize=(70, 40))
plot_tree(dtc, filled=True, feature_names=tr, class_names=dtc.classes_)
plt.show()

# 获取决策树剪枝路径
pruning_path = dtc.cost_complexity_pruning_path(X_train, y_train)
print('ccp_alpha:', pruning_path['ccp_alphas'])
print('impurities:', pruning_path['impurities'])
ccp_alphas, impurities = pruning_path.ccp_alphas, pruning_path.impurities

# 绘制ccp_alpha与impurities的关系
plt.plot(ccp_alphas[:-1], impurities[:-1], marker='o', drawstyle="steps-post")
plt.xlabel("effective alpha")
plt.ylabel("total impurity of leaves")
plt.title("Total Impurity vs effective alpha")

# 获取每个样本所属的叶子节点
leaf_nodes = dtc.apply(X_train)

# 统计每个叶子节点中各类别的样本数量
leaf_samples = {}
for i, leaf in enumerate(leaf_nodes):
    if leaf not in leaf_samples:
        leaf_samples[leaf] = {}
    if y_train.iloc[i] not in leaf_samples[leaf]:
        leaf_samples[leaf][y_train.iloc[i]] = 0
        leaf_samples[leaf][y_train.iloc[i]] += 1

# 计算每个叶子节点中占比最高的类别在该叶子节点中的比例
leaf_ratios = []
for leaf, samples in leaf_samples.items():
    total_samples = sum(samples.values())
    max_class_ratio = max(samples.values()) / total_samples
    leaf_ratios.append(max_class_ratio)

print(leaf_ratios)
summ = 0
for i in leaf_ratios:
    summ = summ + i
print(summ / len(leaf_ratios))

# 显示叶子节点中的分类正确的在总共样本的比例。粗略的可以比较模型的性能。

数据集的头几个数据。

模型的性能。

模型的准确率，ccp_alpha与impurities的关系。

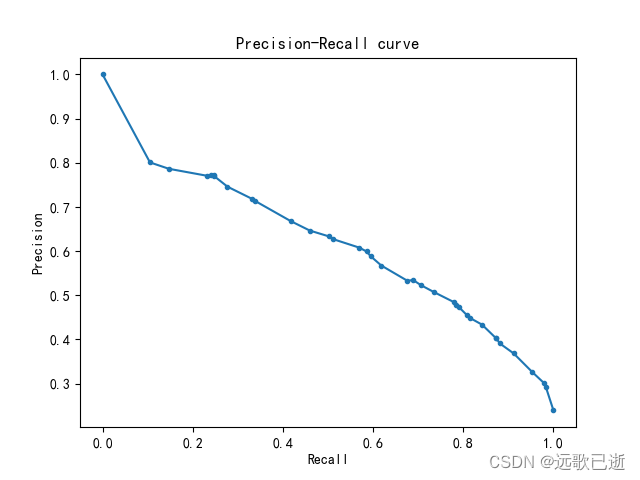
PR曲线的可视化。

决策树可视化。因为为了能看到里边的文字所以性能不是很好。

疑难小结(总结个人在实验中遇到的问题或者心得体会)

数据集的处理上还是有很大的提升空间，首先是数据集总共有好几个表格，我只使用了其中的一个。其次是由于特征太多为了偷懒和绘制决策树就删除了一些，并且尽可能的减少了特征的数量。这两个由于数据集的处理对模型准确度的影响还是很大的。

如果说回到程序本身，其实还有些我实际上没有彻底理解的地方，比如pr曲线和AUC，因为只知道这样写，而不知道为什么这样写。还有ccp_alpha和impurities的关系并不清楚实际上是怎么回事。

如果对这个决策树的整体理解的话，我个人感觉它和我们人类的逻辑比较相似，正如决策这一个词语，就是我们人类去做决策的时候的思考逻辑一样，某个特征对最终结果的影响越大，那么他就会更靠近决策树的树根的位置，在这个因素的影响下，它分类所产生的信息熵会更小。这是我的理解。