数据结构之图

于 2019-02-28 13:02:41 发布
阅读量205 收藏
点赞数
分类专栏： 算法 代码 文章标签： 卡鲁斯卡尔算法 数据结构之图 普里姆算法 图的深度优先遍历 图的广度优先遍历
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/yuanheng19930119/article/details/88022958
版权
本文详细介绍图数据结构的Java实现，包括邻接矩阵存储、基本操作、深度优先与广度优先遍历算法，以及最小生成树算法（普里姆算法与克鲁斯卡尔算法）。通过具体代码实例展示了如何构建和遍历图，以及如何生成最小生成树。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

该博客来源慕课网“数据结构探险之图篇”，慕课网使用C++语言实现，这里改用Java语言实现，这里采用邻接矩阵来保存图的基本关系，该篇博客实现了图的基本操作，广度优先遍历方法（递归和非递归方式），深度优先遍历，最小生成树算法（普里姆算法，卡鲁斯尔算法），算法在代码中已有详细说明

Node.java类为节点类，存储节点的基本信息

Edge.java类为边类，在生成最小生成树时使用

CMap.java类是实现图的基本操作的类，里面封装了操作图的函数

GraphTest.java类是测试类，生成图及深度和广度遍历图

MinimumSpanningTreeTest.java测试克鲁斯卡尔算法生成最小生成树

MinTreeTest2.java测试普里姆算法生成最小生成树

这是该工程的源码下载地址：https://download.youkuaiyun.com/download/yuanhengzhw/10410176

Node.java类
 

package graph;
 
public class Node {
 
	char m_cData;
	boolean m_bIsVisited;
	public Node(char data)
	{
		m_cData=data;
		m_bIsVisited=false;
	}
	public Node()
	{
		m_cData=0;
	}
}

Edge.java类

package graph;
 
public class Edge {
 
	public int m_iNodeIndexA;
	public int m_iNodeIndexB;
	public int m_iWeightValue;
	public boolean m_bSelected;
	public Edge(int m_iNodeIndexA, int m_iNodeIndexB, int m_iWeightValue,
			boolean m_bSelected) {
		this.m_iNodeIndexA = m_iNodeIndexA;
		this.m_iNodeIndexB = m_iNodeIndexB;
		this.m_iWeightValue = m_iWeightValue;
		this.m_bSelected = m_bSelected;
	}	
}

CMap.java类

package graph;
 
import java.util.ArrayList;
import java.util.List;
import java.util.Vector;
 
public class CMap {
 
	private int m_iCapacity;//图中最多可容纳的顶点数
	private int m_iNodeCount;//已经添加的顶点数
	private Node m_NodeArray[];//用来存放顶点的数组
	private int m_Matrix[];//用来存放邻接矩阵
	private Edge m_Edge[];//存放最小生成树的边
	public CMap(int capacity)
	{
		m_iCapacity=capacity;
		m_iNodeCount=0;
		m_NodeArray=new Node[capacity];
		m_Matrix=new int[capacity*capacity];
		m_Edge=new Edge[capacity-1];
	}
	public boolean addNode(Node node)
	{
		if(node==null)
			return false;
		m_NodeArray[m_iNodeCount]=node;
		m_iNodeCount++;
		return true;
	}
	
	public void resetNode()
	{
		for(int i=0;i<m_iNodeCount;i++)
			m_NodeArray[i].m_bIsVisited=false;
	}
	/**
	 * 向有向图中加入值
	 * @param row
	 * @param col
	 * @param val
	 */
	public boolean setValueToMatrixForDirectedGraph(int row,int col,int val)
	{
		if(row<0||row>m_iCapacity)
		{
			return false;
		}
		if(col<0||col>m_iCapacity)
		{
			return false;
		}
		m_Matrix[row*m_iCapacity+col]=val;
		return true;
	}
	/**
	 * 向无向图中加入值
	 * @param row
	 * @param col
	 * @param val
	 * @return
	 */
	public boolean setValueToMatrixForUndirectedGraph(int row,int col,int val)
	{
		if(row<0||row>m_iCapacity)
		{
			return false;
		}
		if(col<0||col>m_iCapacity)
		{
			return false;
		}
		m_Matrix[row*m_iCapacity+col]=val;
		m_Matrix[col*m_iCapacity+row]=val;
		return true;
	}
	/**
	 * 获取邻接矩阵中某个位置的值
	 * @param row
	 * @param col
	 * @return
	 */
	public int getValueFromMatrix(int row,int col)
	{
		if(row<0||row>m_iCapacity)
		{
			return 0;
		}
		if(col<0||col>m_iCapacity)
		{
			return 0;
		}
		return m_Matrix[row*m_iCapacity+col];
	}
	/**
	 * 打印邻接矩阵
	 */
	public void printMatrix()
	{
		for(int i=0;i<m_iCapacity;i++)
		{
			for(int j=0;j<m_iCapacity;j++)
			{
				System.out.print(m_Matrix[i*m_iCapacity+j]+" ");
			}
			System.out.println();
		}
	}
	/**
	 * 深度优先遍历
	 * @param nodeindex
	 */
	public void depthFirstTraverse(int nodeindex)
	{
		int value=0;
		System.out.print(m_NodeArray[nodeindex].m_cData+" ");
		m_NodeArray[nodeindex].m_bIsVisited=true;
		for(int i=0;i<m_iCapacity;i++)
		{
			value=getValueFromMatrix(nodeindex, i);
			if(value!=0)
			{
				if(m_NodeArray[i].m_bIsVisited)
				{
					continue;
				}else{
					depthFirstTraverse(i);
				}
			}
		}
	}
	/**
	 * 广度优先遍历方法1
	 * @param nodeindex
	 */
	public void breadthFirstTraverse(int nodeindex)
	{
		System.out.print(m_NodeArray[nodeindex].m_cData+" ");
		m_NodeArray[nodeindex].m_bIsVisited=true;
		List<Integer> curList=new ArrayList<>();
		curList.add(nodeindex);
		
		breadthFirstTraverseImpl(curList);
	}
	private void breadthFirstTraverseImpl(List<Integer> preList) {		
		int value=0;
		List<Integer> curList=new ArrayList<>();
		for(int j=0;j<preList.size();j++)
		{
			for(int i=0;i<m_iCapacity;i++)
			{
				value=getValueFromMatrix(preList.get(j), i);
				if(value!=0)
				{
					if(m_NodeArray[i].m_bIsVisited)
					{
						continue;
					}else{
						System.out.print(m_NodeArray[i].m_cData+" ");
						m_NodeArray[i].m_bIsVisited=true;
						curList.add(i);
					}
				}
			}
		}
		if(curList.size()==0)
		{
			return;
		}else{
			breadthFirstTraverseImpl(curList);
		}
	}
	/**
	 * 采用队列原理广度优先遍历图
	 * @param nodeindex
	 */
	public void breadthFirstTraverseByQueue(int nodeindex)
	{
		List<Integer> queue=new ArrayList<>();
		queue.add(nodeindex);	
		int value=0;
		while(queue.size()>0)
		{
			//输出出栈节点信息
			Node node=m_NodeArray[queue.get(0)];
			if(!node.m_bIsVisited)
			{
				System.out.print(node.m_cData+" ");
				node.m_bIsVisited=true;
			}
			//出栈
			nodeindex=queue.get(0);
			queue.remove(0);
			
			//寻找node节点下一层且没有被访问的节点
			for(int j=0;j<m_iCapacity;j++)
			{
				if(m_NodeArray[j].m_bIsVisited)
				{
					//节点被访问，不加入队列
					continue;
				}
				value=getValueFromMatrix(nodeindex, j);
				if(value!=0)
				{
					queue.add(j);
				}
			}
		}
	}
	/**
	 * 普里姆生成树
	 * @param nodeIndex
	 */
	public void primTree(int nodeIndex)
	{
		int value=0;
		int edgeCount=0;
		List<Integer> nodeList=new ArrayList<>();
		nodeList.add(nodeIndex);
		m_NodeArray[nodeIndex].m_bIsVisited=true;
		
		List<Edge> nodeEdge=new ArrayList<>();
		
		System.out.println(m_NodeArray[nodeIndex].m_cData+" ");
		//结束条件，边数为m_iCapacity-1结束
		while(edgeCount<m_iCapacity-1)
		{
			int temp=nodeList.get(nodeList.size()-1);
			for(int i=0;i<m_iCapacity;i++)
			{
				value=getValueFromMatrix(temp, i);
				if(value!=0)
				{
					if(m_NodeArray[i].m_bIsVisited)
					{
						continue;
					}else{
						Edge edge=new Edge(temp, i, value, false);
						nodeEdge.add(edge);
					}
				}
			}
			//从被选边集合中找出最小边
			int edgeIndex=getMinEdge(nodeEdge);
			nodeEdge.get(edgeIndex).m_bSelected=true;
			
			//打印信息
			System.out.println(nodeEdge.get(edgeIndex).m_iNodeIndexA+"----->"
					+nodeEdge.get(edgeIndex).m_iNodeIndexB+","
					+nodeEdge.get(edgeIndex).m_iWeightValue);
			
			//加入一条权值最小边
			m_Edge[edgeCount]=nodeEdge.get(edgeIndex);
			edgeCount++;
			
			int nextNodeIndex=nodeEdge.get(edgeIndex).m_iNodeIndexB;
			
			nodeList.add(nextNodeIndex);
			m_NodeArray[nextNodeIndex].m_bIsVisited=true;
			
			System.out.println(m_NodeArray[nextNodeIndex].m_cData);
		}
	}
	/**
	 * 寻找没有被选出的边
	 * @param nodeEdge
	 * @return
	 */
	private int getMinEdge(List<Edge> nodeEdge) {
		
		int minWeight=Integer.MAX_VALUE;
		int edgeIndex=0;
		for(int i=0;i<nodeEdge.size();i++)
		{
			//寻找没有被选出的边
			if(!nodeEdge.get(i).m_bSelected)
			{			
				//判断所选边两端点是否已经被访问，已经被访问则不加入入选边，否则会形成回路，得不到正确结果
				if(m_NodeArray[nodeEdge.get(i).m_iNodeIndexA].m_bIsVisited&&m_NodeArray[nodeEdge.get(i).m_iNodeIndexB].m_bIsVisited)
				{
					continue;
				}
				if(minWeight>nodeEdge.get(i).m_iWeightValue)
				{
					minWeight=nodeEdge.get(i).m_iWeightValue;
					edgeIndex=i;
				}
			}
		}
		if(minWeight==Integer.MAX_VALUE)
		{
			return -1;
		}
		return edgeIndex;
	}
	/**
	 * 克鲁斯卡尔算法生成树
	 */
	public void kruskalTree()
	{
		
		int value=0;
		int edgeCount=0;
		
		//定义存放节点集合的数组
		//List<List<Integer>> nodeSets=new ArrayList<>();
			
		//第一步：取出所用边
		List<Edge> edgeList=new ArrayList<>();
		for(int i=0;i<m_iCapacity;i++)
		{
			for(int j=i+1;j<m_iCapacity;j++)
			{
				value=getValueFromMatrix(i, j);
				if(value!=0)
				{
					Edge edge=new Edge(i, j, value, false);
					edgeList.add(edge);
				}
			}
		}
		//给选出的边排序
		for(int i=0;i<edgeList.size()-1;i++)
		{
			for(int j=i+1;j<edgeList.size();j++)
			{
				if(edgeList.get(i).m_iWeightValue>edgeList.get(j).m_iWeightValue)
				{
					//交换权重
					int temp=edgeList.get(i).m_iWeightValue;
					edgeList.get(i).m_iWeightValue=edgeList.get(j).m_iWeightValue;
					edgeList.get(j).m_iWeightValue=temp;
					//交换节点A
					temp=edgeList.get(i).m_iNodeIndexA;
					edgeList.get(i).m_iNodeIndexA=edgeList.get(j).m_iNodeIndexA;
					edgeList.get(j).m_iNodeIndexA=temp;
					//交换节点B
					temp=edgeList.get(i).m_iNodeIndexB;
					edgeList.get(i).m_iNodeIndexB=edgeList.get(j).m_iNodeIndexB;
					edgeList.get(j).m_iNodeIndexB=temp;				
				}
			}
		}
		//第二步：从所有边中取出组成最小生成树的边
		//1.找到算法结束条件
		int CalculationNum=0;
		while(edgeCount<m_iCapacity-1&&CalculationNum<edgeList.size())
		{
			//2.从边集合中找到最小边
			Edge edge=edgeList.get(CalculationNum);
			CalculationNum++;
			//判断是否形成回路，形成回来选取下一条边
			if(CheckLoop(edgeCount,edge))
			{
				System.out.println("加入边"+edge.m_iNodeIndexA+","+edge.m_iNodeIndexB+"形成回路");
				continue;
			}
			//如果没有形成回路，则将该边信息加入到边信息中
			m_Edge[edgeCount]=edge;
			edgeCount++;
			//输出该边的信息
			System.out.println(m_NodeArray[edge.m_iNodeIndexA].m_cData+"--->"+
					m_NodeArray[edge.m_iNodeIndexB].m_cData+","+
					edge.m_iNodeIndexA+"--->"+
					edge.m_iNodeIndexB+","+
					edge.m_iWeightValue);
		}
	}
	/*
	 * 判断是否形成回路
	 * true代表形成回路
	 * false代表没有形成回路
	 */
	public boolean CheckLoop(int edgeCount,Edge edge)
	{
		List<Integer> loops=new ArrayList<>();
		loops.add(edge.m_iNodeIndexA);
		loops.add(edge.m_iNodeIndexB);
		for(int i=0;i<edgeCount;i++)
		{
			for(int j=0;j<edgeCount;j++)
			{
				Edge temp=m_Edge[j];
				if(temp.m_iNodeIndexA==loops.get(loops.size()-1))
				{
					loops.add(temp.m_iNodeIndexB);
				}else if(temp.m_iNodeIndexB==loops.get(loops.size()-1)){
					loops.add(temp.m_iNodeIndexA);
				}
				if(loops.get(0)==loops.get(loops.size()-1))
					return true;
			}
		}
		return false;
	}
}

GraphTest.java类

package graph;
 
public class GraphTest {
	
	public static void main(String[] args) {
		
		/*
		 * 图的存储 与 图的遍历
		 * 
		 * 			A
		 *        /   \
		 *       B     D
		 *      / \   / \
		 *     C   F G - H
		 *     \   /
		 *       E 
		 */
		CMap cmap=new CMap(8);
		Node nodeA=new Node('A');//0
		Node nodeB=new Node('B');//1
		Node nodeC=new Node('C');//2
		Node nodeD=new Node('D');//3
		Node nodeE=new Node('E');//4
		Node nodeF=new Node('F');//5
		Node nodeG=new Node('G');//6
		Node nodeH=new Node('H');//7
		
		cmap.addNode(nodeA);
		cmap.addNode(nodeB);
		cmap.addNode(nodeC);
		cmap.addNode(nodeD);
		cmap.addNode(nodeE);
		cmap.addNode(nodeF);
		cmap.addNode(nodeG);
		cmap.addNode(nodeH);
		
		cmap.setValueToMatrixForUndirectedGraph(0, 1, 1);
		cmap.setValueToMatrixForUndirectedGraph(0, 3, 1);
		cmap.setValueToMatrixForUndirectedGraph(1, 2, 1);
		cmap.setValueToMatrixForUndirectedGraph(1, 5, 1);
		cmap.setValueToMatrixForUndirectedGraph(3, 6, 1);
		cmap.setValueToMatrixForUndirectedGraph(3, 7, 1);
		cmap.setValueToMatrixForUndirectedGraph(2, 4, 1);
		cmap.setValueToMatrixForUndirectedGraph(5, 4, 1);
		cmap.setValueToMatrixForUndirectedGraph(6, 7, 1);
		
		cmap.printMatrix();
		
			
		//深度优先遍历
		System.out.println("深度优先遍历");
		cmap.depthFirstTraverse(0);
		
		//广度优先遍历方法
		cmap.resetNode();
		System.out.println("\n广度优先遍历方法");
		cmap.breadthFirstTraverse(0);
		
		//采用队列原理广度优先遍历图
		cmap.resetNode();
		System.out.println("\n采用队列原理广度优先遍历图");
		cmap.breadthFirstTraverseByQueue(0);
		
	}
}

MinimumSpanningTreeTest.java类

package graph;
 
public class MinimumSpanningTreeTest {
	
	
	public static void main(String[] args) {
		/*
			     A	
			  /	 |  \
	         B---F---E	
		      \ / \ /	
			   C----D
			A B C D E F			
			0 1 2 3 4 5
						
			A-B  6	A-E  5	A-F  1			
			B-C  3	B-F  2		
			C-F  8	C-D  7			
			D-F  4	D-E  2			
			E-F	9
		 */
		CMap cmap=new CMap(6);
		Node nodeA=new Node('A');//0
		Node nodeB=new Node('B');//1
		Node nodeC=new Node('C');//2
		Node nodeD=new Node('D');//3
		Node nodeE=new Node('E');//4
		Node nodeF=new Node('F');//5
 
		
		cmap.addNode(nodeA);
		cmap.addNode(nodeB);
		cmap.addNode(nodeC);
		cmap.addNode(nodeD);
		cmap.addNode(nodeE);
		cmap.addNode(nodeF);
 
		
		cmap.setValueToMatrixForUndirectedGraph(0, 1, 6);
		cmap.setValueToMatrixForUndirectedGraph(0, 4, 5);
		cmap.setValueToMatrixForUndirectedGraph(0, 5, 1);
		cmap.setValueToMatrixForUndirectedGraph(1, 2, 3);
		cmap.setValueToMatrixForUndirectedGraph(1, 5, 2);
		cmap.setValueToMatrixForUndirectedGraph(2, 5, 8);
		cmap.setValueToMatrixForUndirectedGraph(2, 3, 7);
		cmap.setValueToMatrixForUndirectedGraph(3, 5, 4);
		cmap.setValueToMatrixForUndirectedGraph(3, 4, 2);
		cmap.setValueToMatrixForUndirectedGraph(4, 5, 9);
		
		//普里姆算法
		cmap.primTree(0);
		//克鲁斯卡尔算法
		//cmap.kruskalTree();
		
			
	}	
}

MinTreeTest2.java类

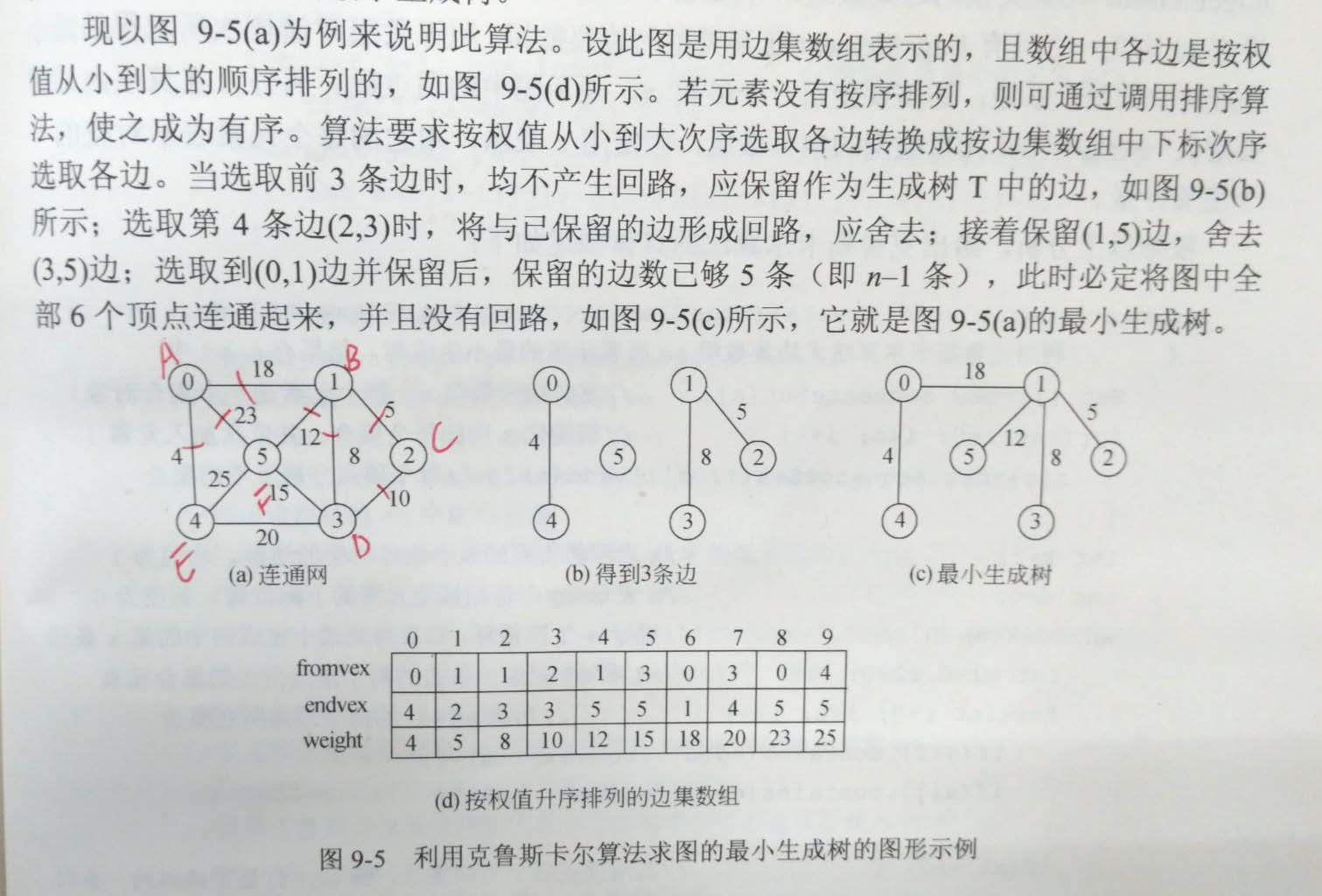
附加卡鲁斯卡尔算法的过程或原理，该类的数据与下图中的数据一致

package graph;
 
public class MinTreeTest2 {
 
	public static void main(String[] args) {
		/*
		 *     A-----B
		 *     |\   /| \
		 *     |  F  |   C
		 *     | / \ | /
		 *     E-----D   
		 */
		CMap cmap=new CMap(6);
		Node nodeA=new Node('A');//0
		Node nodeB=new Node('B');//1
		Node nodeC=new Node('C');//2
		Node nodeD=new Node('D');//3
		Node nodeE=new Node('E');//4
		Node nodeF=new Node('F');//5
 
		
		cmap.addNode(nodeA);
		cmap.addNode(nodeB);
		cmap.addNode(nodeC);
		cmap.addNode(nodeD);
		cmap.addNode(nodeE);
		cmap.addNode(nodeF);
		
		cmap.setValueToMatrixForUndirectedGraph(0, 1, 18);
		cmap.setValueToMatrixForUndirectedGraph(0, 4, 4);
		cmap.setValueToMatrixForUndirectedGraph(0, 5, 23);
		cmap.setValueToMatrixForUndirectedGraph(1, 5, 12);
		cmap.setValueToMatrixForUndirectedGraph(1, 3, 8);
		cmap.setValueToMatrixForUndirectedGraph(1, 2, 5);
		cmap.setValueToMatrixForUndirectedGraph(2, 3, 10);
		cmap.setValueToMatrixForUndirectedGraph(3, 5, 15);
		cmap.setValueToMatrixForUndirectedGraph(3, 4, 20);
		cmap.setValueToMatrixForUndirectedGraph(4, 5, 25);
		//cmap.primTree(0);
		//克鲁斯卡尔算法
		cmap.kruskalTree();
	}
 
}

 

评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值