领略算法真谛:背包问题(完全背包，多重背包)

嘿，各位技术潮人！好久不见甚是想念。生活就像一场奇妙冒险，而编程就是那把超酷的万能钥匙。此刻，阳光洒在键盘上，灵感在指尖跳跃，让我们抛开一切束缚，给平淡日子加点料，注入满满的passion。准备好和我一起冲进代码的奇幻宇宙了吗？Let's go！

我的博客：yuanManGan

我的专栏：C++入门小馆 C言雅韵集 数据结构漫游记  闲言碎语小记坊 题山采玉

之前我们介绍了01背包问题，那就让我们来学习一下，剩下的背包问题吧！

完全背包问题：

 完全背包

题目来源： 牛客网

题目链接：【模板】完全背包

难度系数： ★★

我们完全背包问题和01背包的问题的唯一区别就是完全背包问题可以选择一个物品无限次。

我们重新来分析一下：

1.状态表示

f [ i ][ j]  从前 i 号物品中选，总体积不超过 j 时的最大价值

2.状态转移方程：

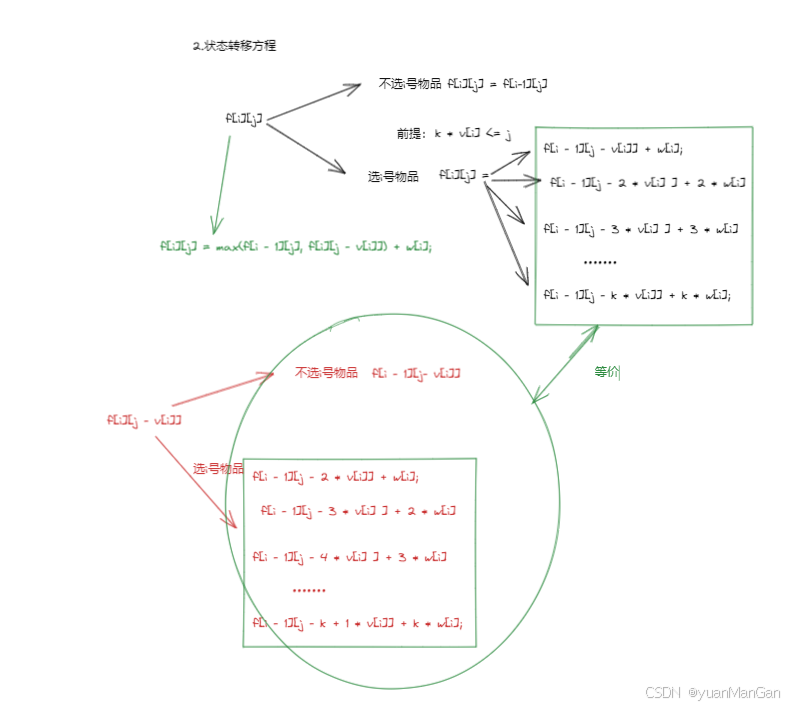
根据上图：

f[i][j] = max(f[i - 1][j], f[i][j - v[i]] + w[i]);

3.初始化：

当i = 0时
        f[i][j] 表示 从前0号物品中选择的体积小于j时的最大价值

所以f[0][0] = 0;不需要初始化

跟01背包一样我们不用初始化。

4.填表顺序。

因为我们要得到本行的左边的值才能填右边，所以我们填j时要从左到右，一样我们要从上到下填表。

5.最终结果

f[n][m].

关于体积刚好等于v时的情况就不赘述了，01背包哪里已经讲的很清楚了。

代码实现：

#include <iostream>
#include <cstring>
using namespace std;
const int N = 1010;
int v[N], w[N];
int f[N][N];
int n, m;
int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i++) cin >> v[i] >> w[i];
    for(int i = 1; i <= n; i++)
    {
        for(int j = 0; j <= m; j++)
        {
            f[i][j] = f[i - 1][j];
            if(j >= v[i]) f[i][j] = max(f[i][j], f[i][j - v[i]] + w[i]);                    
        }    
    }
    cout << f[n][m] << endl;
    
    memset(f, -0x3f, sizeof f);
    f[0][0] = 0;
    for(int i = 1; i <= n; i++)
    {
        for(int j = 0; j <= m; j++)
        {
            f[i][j] = f[i - 1][j];
            if(j >= v[i]) f[i][j] = max(f[i][j], f[i][j - v[i]] + w[i]);                    
        }    
    }
    if(f[n][m] >= 0)
        cout << f[n][m] << endl;
    else
        cout << 0 << endl;
    return 0;
}

空间优化：

一样的这题也有空间优化的方法，但这里和01背包不一样。

我们会用到这一行左边的值，所以我们得先填左边，注意01背包我们是要用到填上一行左边的值，如果先填左边，导致右边的值填的时候找的上一行左边的值已经被覆盖掉了。但完全背包不一样，我们是要用本行的左边，所以得先填左边。希望能够理解清楚这个问题。所以我们填表时得从上到下，从左到右。

代码：

#include <iostream>
#include <cstring>
using namespace std;
const int N = 1010;
int v[N], w[N];
int f[N];
int n, m;
int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i++) cin >> v[i] >> w[i];
    for(int i = 1; i <= n; i++)
        for(int j = v[i]; j <= m; j++)
            f[j] = max(f[j], f[j - v[i]] + w[i]);                    
    cout << f[m] << endl;
    
    memset(f, -0x3f, sizeof f);
    f[0] = 0;
    for(int i = 1; i <= n; i++) cin >> v[i] >> w[i];
    for(int i = 1; i <= n; i++)
        for(int j = v[i]; j <= m; j++)
            f[j] = max(f[j], f[j - v[i]] + w[i]);                    
   
    if(f[m] >= 0)
        cout << f[m] << endl;
    else
        cout << 0 << endl;
    return 0;
}

多重背包问题：

多重背包

题⽬来源： ⽜客⽹

题⽬链接：多重背包

难度系数： ★★

多重背包问题和01背包问题也只有一点区别，多重背包问题每个物品都有最大购买次数。

同样五大步：

1.状态表示

f [ i ][ j]  从前 i 号物品中选，总体积不超过 j 时的最大价值

2.状态转移方程：

但到了这个时候我们就不能像完全背包一样使用f[ i ][ j - v[ i ] ] + w[ i ]来表示那一大串了。

让我们看看f[ i ][ j - v[ i ] ] + w[ i ]与那一大串的区别。

那我们只能老老实实循环k次解决咯。

3.

#include<iostream>
using namespace std;
int n, m;
const int N = 110;
int f[N][N];
int v[N], w[N], x[N];
int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i++) cin >> x[i] >> w[i] >> v[i];   
    
    for(int i = 1; i <= n; i++)
    {
        for(int j = m; j >= 0; j--)
        {
            f[i][j] = f[i - 1][j];
            for(int k = 0; k <= x[i] && j >= k * w[i]; k++) // 修改条件
            {
                f[i][j] = max(f[i][j], f[i - 1][j - k * w[i]] + k * v[i]);    
            }
        }    
    }
     cout << f[n][m] << endl;   
    return 0;
}

空间优化：

#include<iostream>
using namespace std;
int n, m;
const int N = 110;
int f[N];
int v[N], w[N], x[N];

int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i++) cin >> x[i] >> w[i] >> v[i];   

    for(int i = 1; i <= n; i++)
    {
        for(int j = m; j >= 0; j--)
        {
            for(int k = 0; k <= x[i] && j >= k * w[i]; k++) 
            {
                f[j] = max(f[j], f[j - k * w[i]] + k * v[i]);    
            }
        }    
    }
    cout << f[m] << endl;   
    return 0;
}