Radar Installation
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 52282 | Accepted: 11745 |
Description
Assume the coasting is an infinite straight line. Land is in one side of coasting, sea in the other. Each small island is a point locating in the sea side. And any radar installation, locating on the coasting, can only cover d distance, so an island in the sea can be covered by a radius installation, if the distance between them is at most d.
We use Cartesian coordinate system, defining the coasting is the x-axis. The sea side is above x-axis, and the land side below. Given the position of each island in the sea, and given the distance of the coverage of the radar installation, your task is to write a program to find the minimal number of radar installations to cover all the islands. Note that the position of an island is represented by its x-y coordinates.
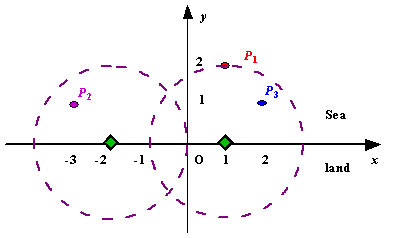
Figure A Sample Input of Radar Installations
We use Cartesian coordinate system, defining the coasting is the x-axis. The sea side is above x-axis, and the land side below. Given the position of each island in the sea, and given the distance of the coverage of the radar installation, your task is to write a program to find the minimal number of radar installations to cover all the islands. Note that the position of an island is represented by its x-y coordinates.

Figure A Sample Input of Radar Installations
Input
The input consists of several test cases. The first line of each case contains two integers n (1<=n<=1000) and d, where n is the number of islands in the sea and d is the distance of coverage of the radar installation. This is followed by n lines each containing two integers representing the coordinate of the position of each island. Then a blank line follows to separate the cases.
The input is terminated by a line containing pair of zeros
The input is terminated by a line containing pair of zeros
Output
For each test case output one line consisting of the test case number followed by the minimal number of radar installations needed. "-1" installation means no solution for that case.
Sample Input
3 2 1 2 -3 1 2 1 1 2 0 2 0 0
Sample Output
Case 1: 2 Case 2: 1
Source
提示:简单的贪心
正确的算法是:要考虑把雷达站放到哪个位置使得包含雷达的区间最多!
写算法的时候要注意,按海岛的横坐标排序(纵坐标是跟随横坐标,但不能对排序构成任何影响)后,第一个雷达建立在区间的右端,然后依次判断每个区间的左端点,如果在最新建立的雷达右面,那么肯定需要一个雷达,而且也建在区间右端。如果左端点在雷达左面,这个时候要考虑区间的右端在雷达的左面还是右面,如果是右面,那雷达位置就不变,如果在左面,那现在的雷达是覆盖不了的,所以要把雷达放在该区间的右端点!因为这样同时不但能覆盖原来的岛,还能覆盖现在的岛
标准方法是把每个点的放置雷达的区间求出,然后按照区间排序。排好序后,从左至右看,当发现下一个区间的起始点大于前面所有区间的最小结束点的时候,答案加一。忽视前面走过的所有点后,对后面进行相同的操作(从左至右看,当发现下一个区间的起始点大于左边未被忽视的所有区间的最小结束点的时候,答案加一)。直到结束。但是这样做相对较难实现。
ac代码#include<stdio.h>
#include<math.h>
#include<stdlib.h>
struct s{
double x,y;
};
int cmp(const void *a,const void *b)
{
if((*(struct s *)a).x>(*(struct s *)b).x)
return 1;
else
return -1;
}
int main()
{
int n,ra,c=0;
while(scanf("%d%d",&n,&ra)!=EOF,n||ra)
{
int i,w=1,num=1;struct s b[10000];
double l[10000],r[10000],temp;
for(i=0;i<n;i++)
{
scanf("%lf%lf",&b[i].x,&b[i].y);
if(b[i].y>ra)
w=0;
}
if(!w)
{
printf("Case %d: -1\n",++c);
continue;
}
qsort(b,n,sizeof(b[0]),cmp);
for(i=0;i<n;i++)
{
l[i]=b[i].x-sqrt(ra*ra-b[i].y*b[i].y);
r[i]=b[i].x+sqrt(ra*ra-b[i].y*b[i].y);
//printf("%lf %lf\n",b[i].x,b[i].y);
}
temp=r[0];
for(i=1;i<n;i++)
{
if(l[i]>temp)
{
temp=r[i];
num++;
}
else if(r[i]<temp)
temp=r[i];
}
printf("Case %d: ",++c);
printf("%d\n",num);
}
}







 探讨了如何使用贪心算法解决雷达安装问题,旨在覆盖海面上的岛屿,需确定最少雷达数量及其最佳位置。
探讨了如何使用贪心算法解决雷达安装问题,旨在覆盖海面上的岛屿,需确定最少雷达数量及其最佳位置。
















 1186
1186

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








