P1087 [NOIP 2004 普及组] FBI 树

题目描述

我们可以把由 0 和 1 组成的字符串分为三类全0串称为B串，全1串称为I串，既含0又含1的串则称为F串。

FBI树是一种二叉树，它的结点类型也包括F结点，B结点和I结点三种。由一个长度为 2^N的01 串 S可以构造出一棵 FBI 树T，递归的构造方法如下：

1. T的根结点为R，其类型与串 S 的类型相同；
2. 若串S的长度大于1，将串S从中间分开，分为等长的左右子串S1和S2；由左子串S1构造R的左子树T1，由右子串S2构造R的右子树T2。

现在给定一个长度为2^N的01 串，请用上述构造方法构造出一棵 FBI 树，并输出它的后序遍历序列。

输入格式

第一行是一个整数 N (0≤N≤10)，  

第二行是一个长度为 2^N 的 01 串。

输出格式

一个字符串，即 FBI 树的后序遍历序列。

输入 #1
3
10001011

输出 #1
IBFBBBFIBFIIIFF

说明/提示

对于40% 的数据，N≤2；

对于全部的数据，N≤10。
noip2004普及组第3题

//思路//

这一题题目描述比较绕，我们来理一下题目意思

首先，要输入n，然后输入长度为2的n次方的一串01数字（也就是根节点R和最后一行的叶节点的所有值）。这里与淘汰赛很像，也是告诉了我们所有的叶节点，让我们把这一棵树复原出来。

所以，让我们来看一下这一题的图

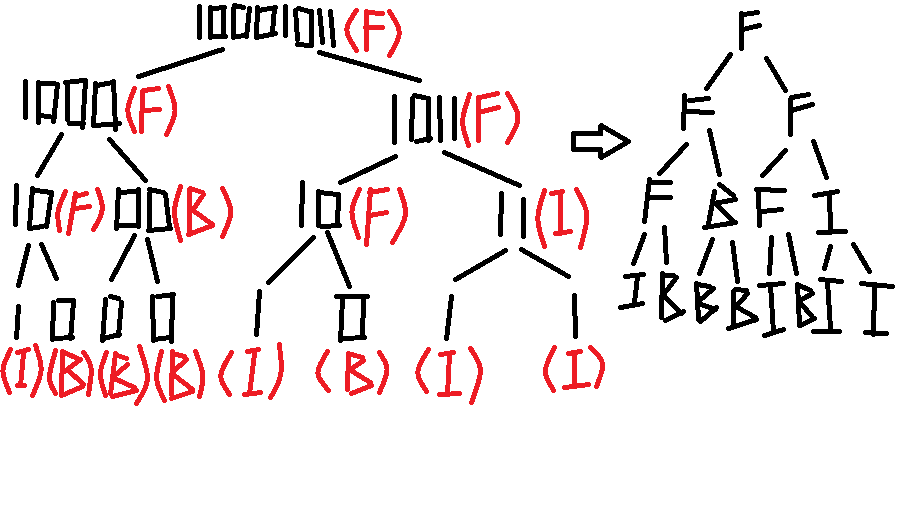在知道这棵树的全貌后，我们就可以求它的后序遍历了。这时候，来了解一下后序遍历怎么求

void dfs(int x) {            //需要用dfs来输出它的后序遍历
	if (x<=...) {            //"..."处要看每一题的条件来写
		dfs(x*2);            //这里是搜右子树
		dfs(x*2+1);          //这里是搜左子树
		cout<<x;             //输出后序遍历
	}
} 

（只是模板，要看每一题的情况来写）

那么，来看一下本题代码

#include<bits/stdc++.h>
using namespace std;
int n,a[2050];               //输入的第一个整数n，用来存树的数组a,因为最大是2的10次方，所以开2050就可以                     
void dfs(int b) {            //输出后序遍历，因为x在下面用来存2的n次方了，所以用b
	if (b<=pow(2,n+1)-1) {   //因为节点最多是2的n+1次方减一，所以“...”处写“pow(2,n+1)-1”，pow是算次方的函数
		dfs(b*2);            //遍历右子树
		dfs(b*2+1);          //遍历左子树
		if (a[b]==0)         //如果它是0
			cout<<"B";       //代表它是“B”树，输出“B”
		else if (a[b]==1)    //如果它是1
			cout<<"I";       //代表它是“I”树，输出“I”
		else                 //如果它是2(01混合串)
			cout<<"F";       //代表它是“F”树，输出“F”
	}
} 
int main(){
	cin>>n;                  //输入n;
	int x=pow(2,n),y=pow(2,n+1)-1;
                             //定义x为2的n次方，y等于2的n+1次方减1
    for (int i=x;i<=y;i++) { //因为它给了所有叶节点，所以从最后一行第一个(2的n次方)到最后一个(2的n+1次方减1)来循环输入
    	scanf("%1d",&a[i]);  //用这个可以一个一个输入，可以方便一点
	}
	for (int i=x-1;i>=1;i--){//从倒数第二行最后一个开始看它(通过它的两个孩子来看它是哪种树)
		if (a[i*2]==0&&a[i*2+1]==0) {
                             //如果它的两个孩子都是0
			a[i]=0;          //那它也是0("B"树)
		}
		else if (a[i*2]==1&&a[i*2+1]==1) {
                             //如果它的两个孩子都是1
			a[i]=1;          //那它也是1("I"树)
		}
		else {               //如果它的两个孩子有0有1
			a[i]=2;          //那它就是2("F"树)
		}
	}
	dfs(1);                  //构建好树之后，输出它的后序遍历
	return 0;
}

大家如果画一个图会更清楚，计算过程太麻烦，就不写了(oﾟvﾟ)