看到一篇很好的入门文章,A Quick Introduction to Neural Networks。作者ujjwalkarn,文章浅显易懂的介绍了神经网络的基本构架、神经网络中的基本概念,并通过多层感知机举例说明了正向传播和反向传播算法,看了一遍原文,受益颇丰,自己翻译一遍,加深印象,因水平有限,翻译不当之处恳请指正,我会很开心的接受批评,绝不翻脸!!!!!(╯‵□′)╯︵┻━┻
###############################################################################
简介神经网络
人类脑海中的生物神经元处理信息的方式给予了科学家灵感,以此研究出了人工神经网络(ANN),它是一种用于数学计算的模型。得益于这个人工模型,使得语义识别、计算机视觉和文本处理这些领域有了突破性进展,也让人们对机器学习领域产生了极大的兴趣。这篇博文我们想向大家科普一个优点特殊的人工神经网络模型——多层感知机(MLP)。
单一神经元
在神经网络中用于计算的最基本单元叫做神经元,通常也称为节点或单元。它接收来自其它神经元的输入或者接收外部的输入同时将这些输入通过计算再次输出。每一个输入都有一个与之相对的权重(W),这个权重表示这个输入相比于其他输入的重要性的大小。在这个神经元中,会定义一个函数f(如下图所示)来计算输入再加权求和之后的结果,如图1所示。
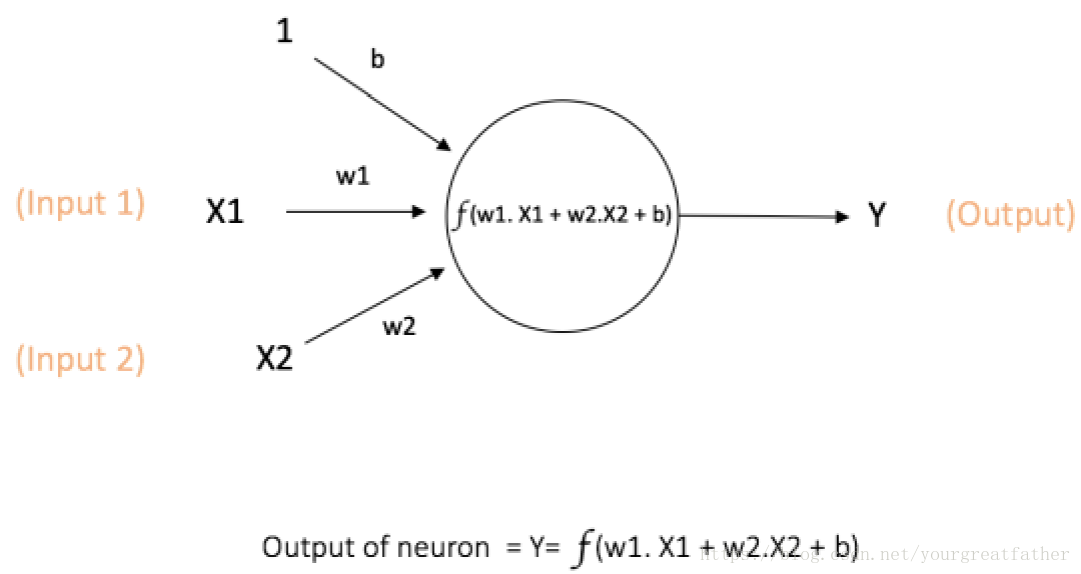
图1:一个单一神经元
图中的神经元中X1、X2作为输入,同时每一个输入对应一个权值w1和w2。此外,还有一个输入1对应的权值为b(我们称其为偏差bias)。有关偏差的更多细节我们随后再说。
神经元的输出Y通过图1所示的方式进行计算。其中函数f是一个非线性函数,我们称作激活函数(activation function)。引入激活函数的目的是为了产生非线性的输出结果。这一点非常重要,因为日常生活中的数据大多是非线性的,因此我们需要我们的神经元可以习得非线性的结果。
每一个激活函数(非线性函数)都会读取一个数作为输入,并对这个输入进行某种特定的数学操作。下面列出一些未来学习中大家可能会遇到的激活函数:
○ Sigmoid:读取一个实数(实值?)作为输入,并将输出∈(0,1)的值。
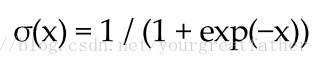
○ tanh:读取一个实数(实值?)作为输入,并将输出∈[-1,1]的值。
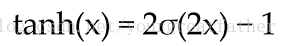
○ ReLU:ReLU是修正过的线性函数(Rectified Liner Unit),它读取一个实数作为输入,并将最小的阈值控制为0(非负,用0替代了负值)。
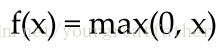
图2显示了上方所述的不同激活函数的图形。
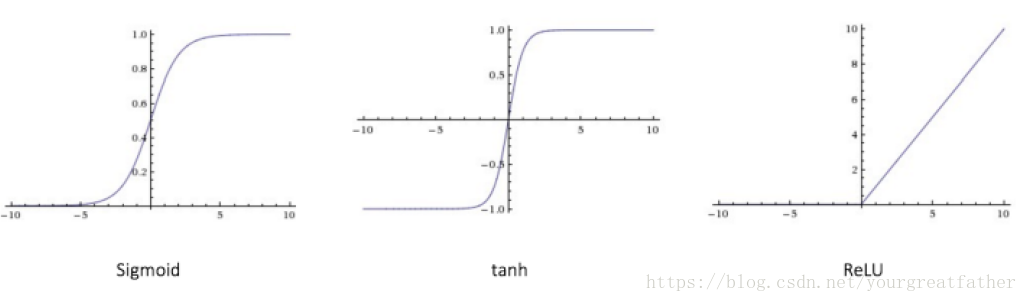
图 2 不同的激活函数
偏差的重要性:偏差最主要的功能是给每一个节点提供一个可以用于训练的常值(除了节点接收到的正常输入之外的)。戳这个链接了解神经元中偏差更多的作用。(链接还没啃,先放在这里)
前馈神经网络
前馈神经网络是人工神经网络设计中最初和最简单的神经网络类型。它包含分布在不同层之间的多个神经元(节点)。相邻的层之间的节点相互连接或者拥有edges(这里不知如何翻译)。每一个连接都有与之相对应的权值。
图3举例说明了一个前馈神经网络。
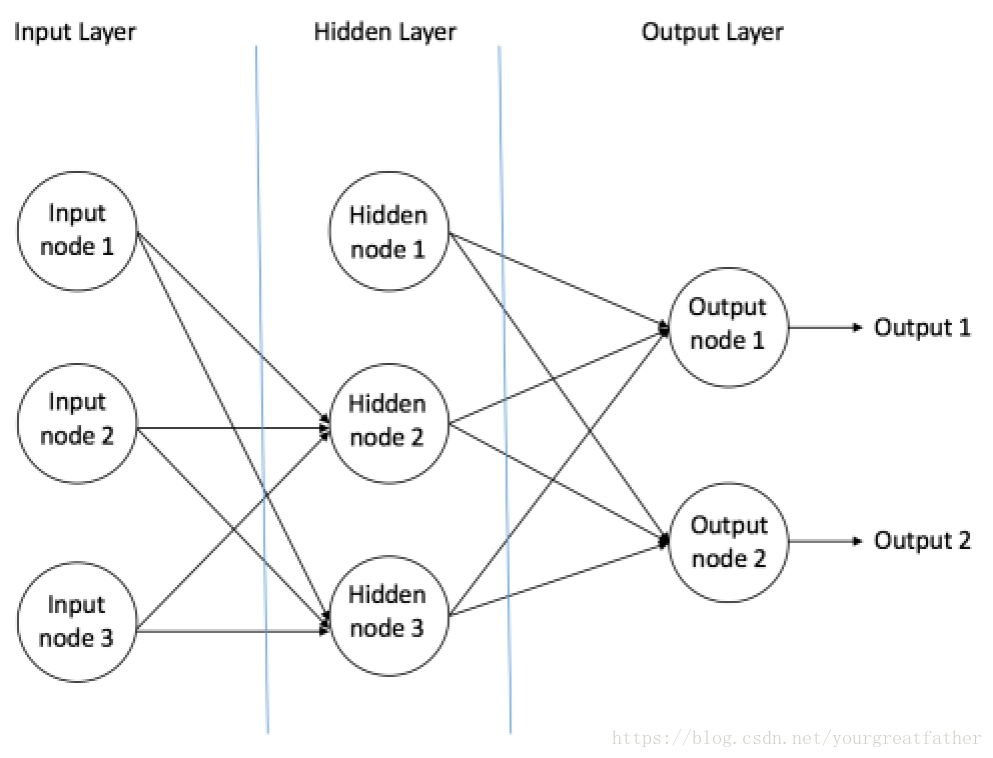
图 3 前馈神经网络举例
一个前馈神经网络可以有三种神经元组成:
1.输入节点——输入节点将外界的信息输入到神经网络中,而所有的输入节点共同组成了“输入层”。在输入节点中没有任何数学运算,它们仅仅用于将信息传入隐藏节点。
2.隐藏节点——隐藏节点与外界没有直接的连接(因此称作“隐藏的”)。它们进行数学运算,并将从输入节点得到的信息转移到输出节点中。所有的隐藏节点共同组成了“隐藏层”。一个前馈神经网络仅可拥有一个输入层和一个输出层,但却可以拥有0至多个隐藏层。
3.输出节点——所有的输出节点共同组成了“输出层”,输出节点负责数学运算,并将结果向外界输出。
在前馈神经网络中,信息传播的方向仅有一个,那就是——“前向”,也就是从输入节点,通过隐藏节点(如果有的话)传递到输出节点。在神经网络中没有循环或者闭环(这一特性使得前馈神经网络与循环神经网络RNN中组成闭环的神经元差别很大)。
下面举两个前馈神经网络的例子:
1.单层感知机——这是最简单的前馈神经网络,它没有隐藏层。你可以通过参考文献[4]、[5]、[6]、[7]做更多的了解。
2.多层感知机——多层感知机拥有一个或多个隐藏层。我们接下来仅讨论多层感知机,因为在今天的实际运用中,多层感知机比单层感知机适用范围更广泛。
多层感知机
一个多层感知机(MLP)拥有一个或者多个隐藏层(除了一个输入层和一个输出层)。单层感知机仅可以习得线性函数,但是多层感知机却可以习得非线性函数。
图4展示了一个仅有一个隐藏层的多层感知机。需要注意的是,每一个连接都有与之相对应的权值,但图中仅列出了w0,w1,w2。
输入层:输入层有三个节点。偏差节点的值为1。其他两个节点将X1,X2作为外部输入(它们都是数字量,取值取决于输入的数组)。正如上文所说,在输入层不进行数字运算,因此输入层中每个节点的相应输出结果分别为1,X1,X2,这些结果紧接着被喂入隐藏层。
隐藏层:隐藏层同样拥有三个节点,其中偏差节点的值为1。隐藏层中其他两个节点的输出结果取决于输入层的输出结果(1,X1,X2)和相对应的权重值。图4中凸出显示了隐藏层中一个节点的计算结果。同样的,其他隐藏节点的输出值也可以被计算出来。要记住,f代表的是激活函数。这些计算结果随后被喂入输出层的的节点中。
输出层:输出层有两个节点,它们从隐藏层获得输入然后进行如图中凸出显示部分一样的计算。计算出来的结果(Y1和Y2)作为本层的输出,同时也是多层感知机的输出结果。
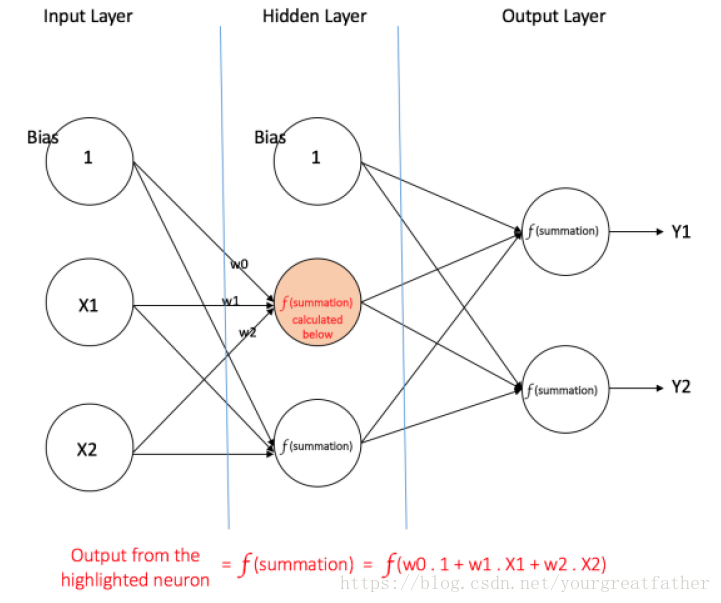
图 4 拥有一个隐藏层的多层感知机
给定一个特征数组X=(X1,X2,...)和一个目标y,多层感知机可以习得特征数组与目标之间的关系,随后进行分类或者回归(?)。
让我们举个例子以便于更好的理解多层感知机。假设我们有如下一个关于学生成绩的数组:
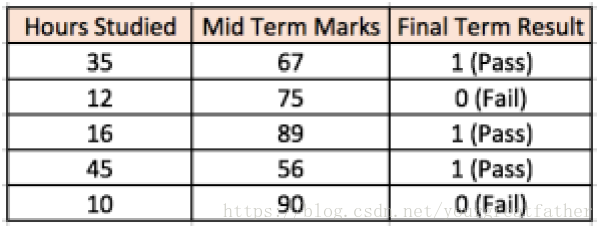
两个输入栏分别是学生学习的时间和期中考试获得的考试成绩。最后的结果栏显示的是两个值1或者0代表学生是否通过了期末考试。例如,我们可以发现假如一个学生学习了35个小时,期中考试获得了67分,他/她最后通过了期末考试。
现在,假设,我们想预测一个学习了25个小时,期中考试获得70分的学生能否通过期末考试呢?

这是一个二元分类问题,多层感知机可以从所给的事例中(训练集)进行学习,并对新的数据进行预测。接下里我们说说多层感知机是如何习得训练集和预测结果直接的关系的。
训练我们的多层感知机:反向传播算法
多层感知机学习的方法叫做反向传播算法。这里引用Quora上Hemanth Kumar的回答,戳这里,他的回答解释的很清晰,当然,我们引用如下。
一个ANN由节点组成的不同层组成;输入层,中间的隐藏层(们【是不是感觉这个们很精辟,( ̄▽ ̄)/,诠释了英语里的s】)还有输出层。相邻的层之间相连的节点都有与之相对应的权值。学习的目标就是为每一个连接(edge的猜测)找到正确的权值。给定一个输入向量,这些权值决定了输出向量是什么。
在监督学习中,训练集是给定标签的(标注好的)。这意味着,对于一些给定的输入,我们知道我们想要的/预期的输出结果(标签)。
BackProp算法:
最初,每一个连接的权值都是随机赋予的。对于每一个训练集的输入,ANN都会作出反应,它的每一个输出都会被观察。这些输出结果会与我们预期的输出结果进行比对,其中的误差会被“传播”回上一层。这些误差将被“关注”,并且权值会相应的作出“调整”。这个步骤会重复多次,直到误差降低到我们预期的阈值以下。
一旦上述算法结束,我们就有了一个“学习过”的ANN,这个ANN就可以用于我们需要的“新”输入(的预测)。这个ANN就是我们所说的通过几个样例(有标签的数据)和它自身的错误(误差传播)学习过的ANN。
现在我们了解了反向传播是如何工作的,让我们回到先前说过的学生成绩数据组。
多层感知机如图5所示(图源),在输入层拥有两个节点(不算偏差节点),分别用于输入“学生学习时间”和“中期考试成绩”。同时它还拥有一个含有两个节点的隐藏层(不算偏差节点)。输出层也有两个节点——上方的节点输出“通过”考试的可能性,下方节点输出“未通过”考试的可能性。
在分类任务中,我们通常在多层感知机中使用Softmax函数作为输出层的激活函数,这样保证输出的结果是可能性,并且可能性之和为1。Softmax函数将任意的实数矢量作为输入,其输出结果介于[0,1]之间,并且所有的结果之和为1。因此,在这个例子中: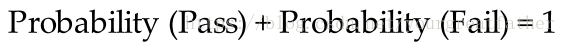
第一步:前向传播
神经网络中所有的权值都是随机赋值。让我们以图5中隐藏层中标记为V的节点为对象。假设,输入进这个节点的相关权值分别为w1,w2,w3(如图)。
神经网络随后读取第一个例子(那就是输入为35和67,输出通过的可能性为1)。
○ 输入神经网络=[35,67]
○ 预期的输出结果(目标)=[1,0]
那么,V节点的输出结果计算如下(f是激活函数,比如sigmoid函数):
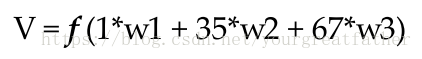
同样的,隐藏层中其他节点的输出结果同样可以计算。隐藏层中两个节点的输出结果将被作为输出层中的输入值。这使得我们可以计算出输出层中两个节点输出的可能性。
假设输出层两个节点输出的结果分别为0.4和0.6(由于权值是随机赋予的,因此结果也具有随机性)。我们可以看到计算出的可能性(0.4和0.6)距离我们期望的可能性(1和0)十分遥远,因此图5中的神经网络拥有一个“错误的输出”。
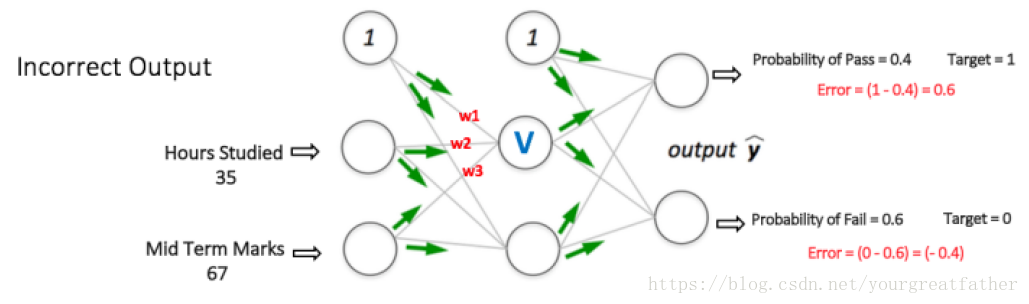
图 5:多层感知机中前向传播的步骤
第二步:反向传播&权值的更新
我们计算出了输出节点中的总体误差,并通过反向传播在神经网络中进行回退,从而计算出梯度差。之后,我们通过最佳的方法,例如梯度下降法,来“调整”所有的权值,目的是是的输出层中的误差最小化。这一过程通过图6展现(暂时忽视掉图中的数学等式)。
假设,现在V节点对应的权值变为w4,w5,w6(经过反向传播和调整权值后)
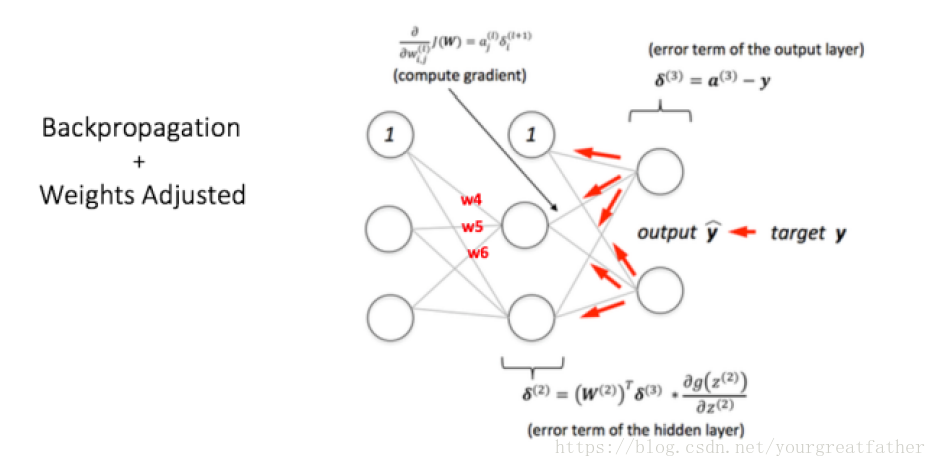
图 6:多层感知机中反向传播和权值更新步骤
如果此时我们再次将同一个样例输入神经网络,那么神经网络的表现将会比刚才好,因为我们经过调整权值使得预测结果的误差变小了。如图7所示,现在误差由之前的[0.6,-0.4]减小到了[0.2,-0.2]。这意味着我们的神经网络此刻已经习得如何正确分类我们第一个训练样本。
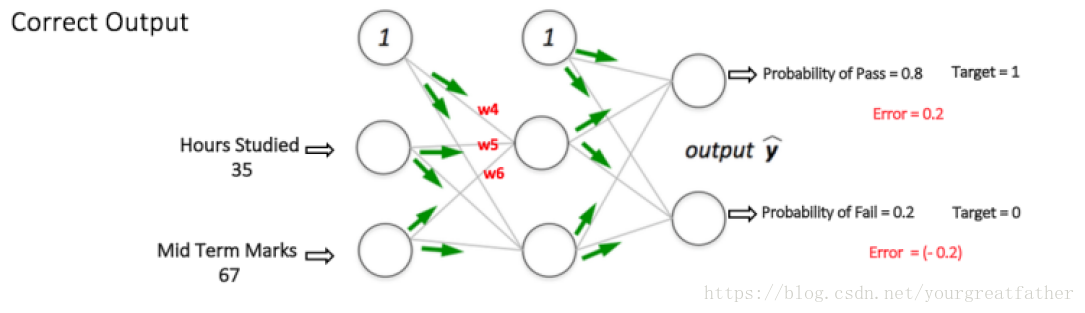
图 7:MLP神经网络在相同输入下比先前表现更好
我们将这一步骤在我们数据集中所有的样例中进行重复。之后,我们就可以说我们的神经网络已经习得了这些样例。
现在,如果我们想知道一个学习了25个小时,期中考试为70分的学生能否通过期末考试,那么我们仅需进行前向传播步骤最后查看输出的通过和不通过的可能性即可。
这篇博客中我避开了罗列数学公式和展开讨论梯度下降法的详细内容,仅仅是为了给读者对于算法一个直观的想法。如果你想获得更多数学层面对于反向传播算法的内容,戳这里。
多层感知机的3D可视化
亚当哈利创造出了一个通过MNIST手写数字数据库训练的多层感知机(通过反向传播)的3D可视化模型,链接在此(需要科学上网)。【墙内的我看不到,如果你看到了可以截图给我看吗?(✧◡✧)】
神经网络将MNIST手写数据集中28*28像素的图片的像素转换为784个数字像素值作为输入(这个神经网络的输入层中拥有784个神经元分别对应784个像素值)。此外在第一个隐藏层中拥有300个神经元,第二个隐藏层中拥有100个神经元,而在输出层中拥有10个神经元(它们与十个输出结果相对应【0,1,2,3,4,5,6,7,8.9】)。
虽然这个神经网络相比于我们之前举例说明的神经网络要大很多(它有更多的隐藏层和神经元),但是在这个神经网络中,前向传播步骤与反向传播步骤都是和先前所说的是相同的。
图8展示了当我们向神经网络输入数字“5”时的情形。
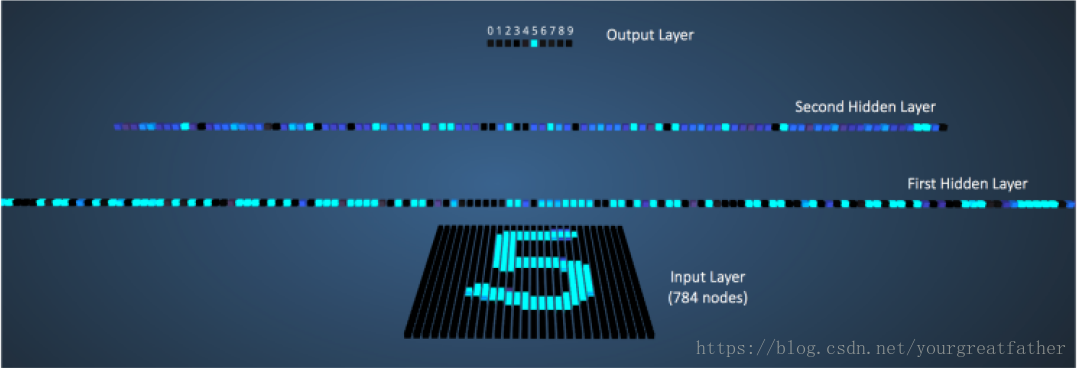
图 8:输入数字“5”时神经网络的可视化
那些拥有更高输出值的神经元我们用更明亮的颜色表示。在输入层,那些明亮的节点是从外部获得更高数字像素值的节点。需要注意在输出层,唯一一个高亮节点与数字5相对应(它(数字5)获得的输出可能性为1,相比于其它数字的输出可能性0要大得多)。这意味着MPL成功对输入数字进行了分类。我非常推荐使用这个可视化模型进行观察,找出不同层之间神经元的连接方式。


























 8万+
8万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








