排序算法详解与优化-优快云博客

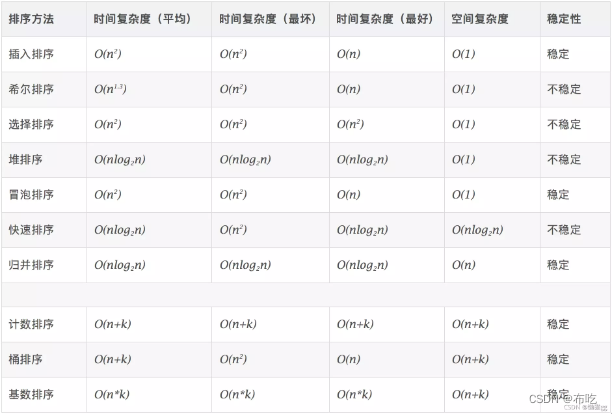
排序算法分类

排序算法可以分为两大类：比较排序和非比较排序
比较排序：可以分为交换排序，插入排序，选择排序和归并排序
交换排序：冒泡排序和快速排序
插入排序：简单插入排序、希尔排序
选择排序：简单选择排序、堆排序
归并排序：二路归并排序、多路归并排序
分比较排序：可以分为计数排序，桶排序和基数排序；
一共是11种排序；
在这里插入图片描述

题目

给你一个整数数组 nums，请你将该数组升序排列。

冒泡排序

概念：把最大的换到最后一位，第二大的换到倒数第二位；

冒泡写法：

//原始写法，每一遍都交换n次
public int[] maopao(int[] nums){
    for(int i=0;i<nums.length-1;i++){
        //int max = 0;
        for(int j=i+1;j<nums.length;j++){
            if(nums[i]>nums[j]){
              int tmp = nums[i];
              nums[i] = nums[j];
              nums[j] = tmp;
            }
        }
    }
    return nums;
}

//优化内循环，交换一次，每次只交换一次
public int[] maopao(int[] nums){
    for(int i=0;i<nums.length-1;i++) {
        int max = 50000, idx = 0;
        for (int j = i + 1; j < nums.length; j++) {
            if (nums[j] < max) {
                max = nums[j];
                idx = j;
            }
        }
        if(nums[i]>max){
            int tmp = nums[i];
            nums[i] = nums[idx];
            nums[idx] = tmp;
        }
    }
    return nums;
}

//优化三 ，对已经有序的序列停止排序
public static void MaoPao(int[] arr) {
		int length = arr.length;
		boolean flag = true;
		//外层循环控制轮数：
		for (int i = 0; i < length - 1; i++) {
			  //内存循环进行比较：
			  //如果内循环整个一轮下去，一次交换也没有发生，
              //说明此时0~length-1-i之间的元素都已经是有序(升序)的了，
			  // 而且我们也知道length-1-i~length-1之间的元素也是刚刚冒泡排序好的有序序列，
			  // 那么此时说明，整个数组其实都已经是有序的了，就没有必要再继续遍历和比较下去了。
			  for (int j = 0; j < length - 1 - i; j++) {
					if (arr[j] > arr[j + 1]) {
						  int temp = arr[j];
						  arr[j] = arr[j + 1];
						  arr[j + 1] = temp;
						  flag = false;
					}
			  }
			  //所以我们设置一个flag，如果内循环整个一轮下去，一次交换也没有发生的时候，flag为true，跳出所有循环；
			  if (flag) {
					break;
			  }
		}
  }

上面是最原始的冒泡和对冒泡优化后的两种算法，极端情况下这两种算法在对数组排序后都会超时；这时候就要考虑同为交换排序的快速排序；

快速排序

概念：选定一个标准值，比这个标准值大的放在右边，小的放在左边；

   public void  quickSort(int[] nums,int left,int right) {
        if(left>=right){
            return;
        }
        int le = left;
        int ri = right;
        //getMid(nums,left,right);
        int povit = nums[left];

        while (le< ri) {
            while (povit <= nums[ri] && le < ri) ri--;
            swap(nums,le,ri);
            while (nums[le] <= povit && le < ri) le++;
            swap(nums,le ,ri);
        }
        nums[le] = povit;
        quickSort(nums,left,le-1);
        quickSort(nums,le+1,right);

    }
    public void swap(int[] nums,int a,int b){
        int tmp = 0;
        if(nums[a]>nums[b]){
            tmp = nums[a];
            nums[a] = nums[b];
            nums[b] = tmp;
        }
    }

简单插入排序

概念：使用双层for循环实现，外层for循环实现n+1的遍历（n是前面已经有序的数组，1是新增要排序的数据），内层for循环实现对插入位置的查找；
代码如下：

public void  chaRu(int[] nums){
		int l = nums.length;
		for(int i =0 ;i<l;i++){
			int tmp = nums[i];
			int j = i-1;
			while(j>=0 && nums[j]>tmp){
				nums[j+1] = nums[j];
				j--;
				}
			nums[j+1] = tmp;
		}
	}

在这里插入图片描述

希尔排序

概念：是按照不同步长对元素进行插入排序，将整个有序序列分割成若干个子序列分别进行插入排序；
代码如下：

public void xier(int[] nums){
		int l = nums.length;
		for(int dk= l/2;dk>=1;dk = dk/2){
			for(int i =dk ;i<l;i++){
				int tmp = nums[i];
				int j = i-dk;
				while(j>=0 && nums[j]>tmp){
					nums[j+dk] = nums[j];
					j=j-dk;
					}
				nums[j+dk] = tmp;
			}
		}
	}

选择排序

原理：先扫描整个数组，已找到最小元素并将这个元素与第一个元素交换；然后从最第二个元素开始扫描找出最小元素与第二数交换；不断重复这个过程；
代码如下(不要和冒泡排序搞混了)：

public void xuanze(int[] nums){
		int l = nums.length;
		for(int i=0;i<l-1;i++){
			int min = 50000,idx=0;
			for(int j =i+1;j<l;j++){
				if(nums[j]<min)
					idx = j;
					min = nums[j];
			}
			if(min<nums[i]){
				int tmp = nums[i];
				nums[i] = nums[idx];
				nums[idx] = tmp;
			}
		}
	}

堆排序

概念：堆是一种叫做完全二叉树的数据结构，可以分为大根堆，小根堆，而堆排序就是基于这种结构而产生的一种算法
原理：大根堆每个节点的值都大于或者等于子节点左右孩子节点的值
小根堆每个节点都小于或者等于子节点左右孩子节点的值
排序思想:
(1)首先将代排的数组构成一个大根堆，此时，整个数组的最大值就是堆结构的顶端
(2)将顶端的数与末尾的数交换，此时，末尾的数为最大值，待排序列长度为n-1；
(3)将剩下的n-1个数重构大根堆。在将顶端数与n-1位置的数进行交换，如此反复执行便能得到有序数组。
代码如下：

 //堆排序
   void adjust(vector<int> &nums, int len, int index){
        int left = 2*index + 1; // index的左子节点
        int right = 2*index + 2;// index的右子节点
        int maxIdx = index;
        if(left<len && nums[left] > nums[maxIdx])     maxIdx = left;
        if(right<len && nums[right] > nums[maxIdx])     maxIdx = right;
 
    if(maxIdx != index)
    {
        swap(nums[maxIdx], nums[index]);
        adjust(nums, len, maxIdx);
    }
 
}
 
// 堆排序
    void HeapSort(vector<int> &nums, int size){
       for(int i=size/2 - 1; i >= 0; i--){
            adjust(nums, size, i);
        }
         for(int i = size - 1; i >= 1; i--){
                swap(nums[0], nums[i]);        
                adjust(nums, i, 0);              
            }
        }
};

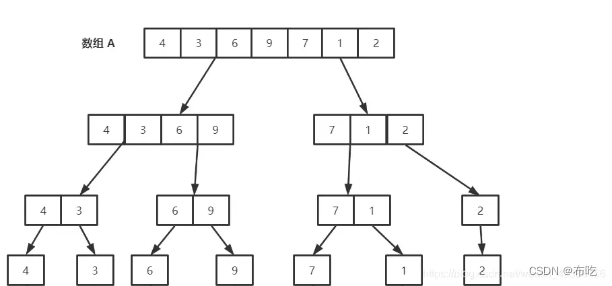
二路归并排序

概念和原理：二路归并排序又称合并排序
图片:
在这里插入图片描述

void mergeSortInOrder(int[] arr,int bgn,int mid, int end){
        int l = bgn, m = mid +1, e = end;
        int[] arrs = new int[end - bgn + 1];
        int k = 0;
        while(l <= mid && m <= e){
            if(arr[l] < arr[m]){
                arrs[k++] = arr[l++];
            }else{
                arrs[k++] = arr[m++];
            }
        }
        while(l <= mid){
            arrs[k++] = arr[l++];
        }
        while(m <= e){
            arrs[k++] = arr[m++];
        }
        for(int i = 0; i < arrs.length; i++){
            arr[i + bgn] = arrs[i];
        }
    }
     void mergeSort(int[] arr, int bgn, int end)
    {
        if(bgn >= end){
            return;
        }
        int mid = (bgn + end) >> 1;
        mergeSort(arr,bgn,mid);
        mergeSort(arr,mid + 1, end);
        mergeSortInOrder(arr,bgn,mid,end);
    }

归并排序和堆排序都是使用了回溯的方法，在实际过程中回溯很有可能代表着超时，那么两种算法就了解即可。