目录
1 . 什么是指数加权平均?
指数加权平均(exponentially weighted averges),也叫指数加权移动平均,是一种常用的序列数据处理方式。
它的计算公式如下:
其中,
- θ_t:为第 t 天的实际观察值,
- V_t: 是要代替 θ_t的估计值,也就是第 t 天的指数加权平均值,
- β: 为 V_{t-1}的权重,是可调节的超参。( 0 < β < 1 )
例如:
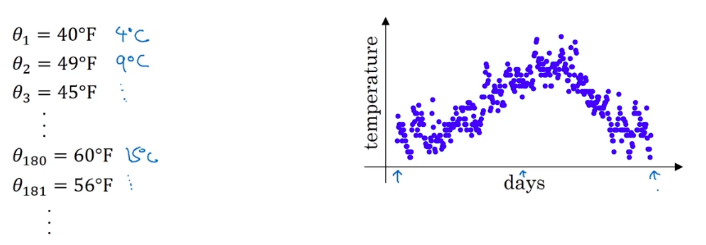
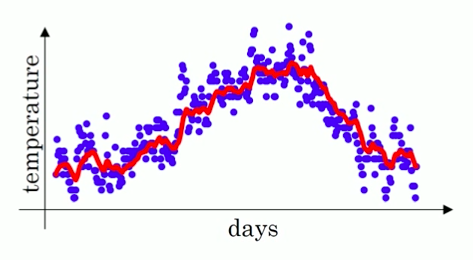
我们有这样一组气温数据,图中横轴为一年中的第几天,纵轴为气温:
直接看上面的数据图会发现噪音很多,
这时,我们可以用 指数加权平均 来提取这组数据的趋势,
按照前面的公式计算:
这里先设置 β = 0.9,首先初始化 V_0 = 0,然后计算出每个 V_t:
将计算后得到的 V_t表示出来,就得到红色线的数值:
可以看出,红色的数据比蓝色的原数据更加平滑,少了很多噪音,并且刻画了原数据的趋势。
指数加权平均,作为原数据的估计值,有以下优点:
1. 抚平短期波动,起到了平滑的作用,
2. 还能够将长线趋势或周期趋势显现出来。
所以应用比较广泛,在处理统计数据时,在股价等时间序列数据中,CTR 预估中,美团外卖的收入监控报警系统中的 hot-winter 异常点平滑,深度学习的优化算法中都有应用。
2 . 为什么在优化算法中使用指数加权平均?
2. 为什么在优化算法中使用指数加权平均
上面提到了一些 指数加权平均 的应用,这里我们着重看一下在优化算法中的作用。
以 Momentum 梯度下降法为例,
Momentum 梯度下降法,就是计算了梯度的指数加权平均数,并以此来更新权重,它的运行速度几乎总是快于标准的梯度下降算法。
这是为什么呢?
让我们来看一下这个图,
例如这就是我们要优化的成本函数的形状,图中红点就代表我们要达到的最小值的位置,
假设我们从左下角这里出发开始用梯度下降法,那么蓝色曲线就是一步一步迭代,一步一步向最小值靠近的轨迹。可以看出这种上下波动,减慢了梯度下降法的速度,而且无法使用更大的学习率,因为如果用较大的学习率,可能会偏离函数的范围。
如果有一种方法,可以使得在纵轴上,学习得慢一点,减少这些摆动,但是在横轴上,学习得快一些,快速地从左向右移移向红点最小值,那么训练的速度就可以加快很多。
这个方法就是动量 Momentum 梯度下降法,它在每次计算梯度的迭代中,对 dw 和 db 使用了指数加权平均法的思想,
这样我们就可以得到如图红色线的轨迹:
可以看到:
纵轴方向,平均过程中正负摆动相互抵消,平均值接近于零,摆动变小,学习放慢。
横轴方向,因为所有的微分都指向横轴方向,因此平均值仍然较大,向最小值运动更快了。
在抵达最小值的路上减少了摆动,加快了训练速度。
3 . β 如何选择?
根据前面的计算式子:
将 V_{100}展开得到:
这里可以看出,V_t是对每天温度的加权平均,之所以称之为指数加权,是因为加权系数是随着时间以指数形式递减的,时间越靠近,权重越大,越靠前,权重越小。
再来看下面三种情况:
当 β = 0.9 时,指数加权平均最后的结果如图红色线所示,代表的是最近 10 天的平均温度值;
当 β = 0.98 时,指结果如图绿色线所示,代表的是最近 50 天的平均温度值;
当 β = 0.5 时,结果如下图黄色线所示,代表的是最近 2 天的平均温度值;
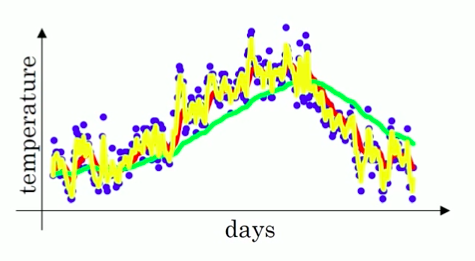
β 越小,噪音越多,虽然能够很快的适应温度的变化,但是更容易出现奇异值。
β 越大,得到的曲线越平坦,因为多平均了几天的温度,这个曲线的波动更小。
但有个缺点是,因为只有 0.02 的权重给了当天的值,而之前的数值权重占了 0.98 ,
曲线进一步右移,在温度变化时就会适应地更缓慢一些,会出现一定延迟。通过上面的内容可知,β 也是一个很重要的超参数,不同的值有不同的效果,需要调节来达到最佳效果,一般 0.9 的效果就很好。





 本文详细解释了指数加权平均的概念及其在优化算法中的关键作用,特别是Momentum梯度下降法中,通过减少梯度的波动,加速训练过程。同时,探讨了超参数β的选择对数据平滑的影响。
本文详细解释了指数加权平均的概念及其在优化算法中的关键作用,特别是Momentum梯度下降法中,通过减少梯度的波动,加速训练过程。同时,探讨了超参数β的选择对数据平滑的影响。
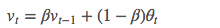
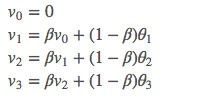



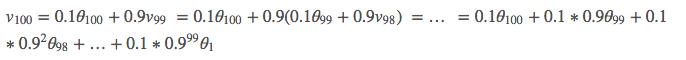

















 4376
4376

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








