数据结构与算法基础课程学习

1. 算法基础概念

1.1 描述

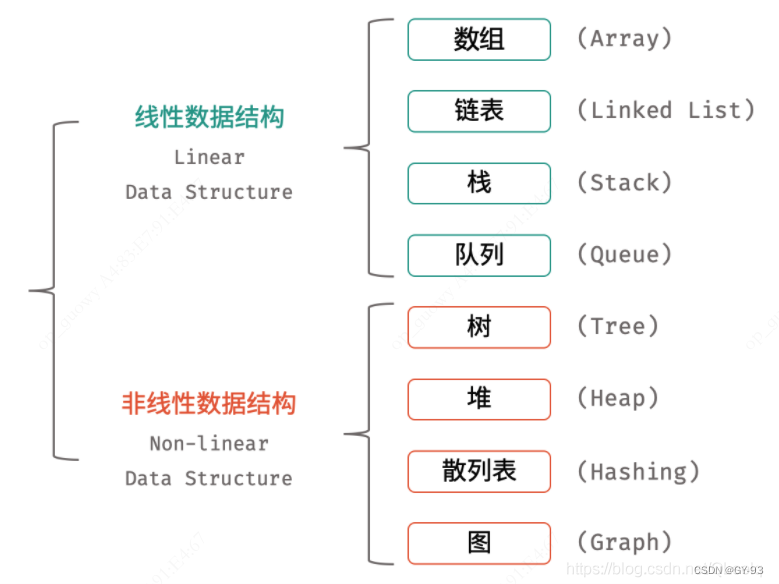
• 算法是指对特定问题求解步骤的一种描述。算法具有以下特性：
  • 有穷性： 算法是由若干条指令组成的有穷序列，总是在执行若干次后结束，不可能永不停止
  • 确定性： 每条语句都有确定的含义，无歧义。
  • 可行性： 算法在当前环境条件下可以通过有限的次数运算实现。
  • 输入输出： 有零个或多个输出，一个或多个输出

1.2 如何判断一个算法写的好不好？

• “好”算法的标准如下：
  • 正确定：正确性是指算法能够满足具体问题的需求，程序运行正常，无语法错误，能够通过典型的软件测试，达到预期的需求
  • 易读性：算法遵循表示符命名规则，简洁易懂
  • 健壮性：算法对非法数据及操作有较好的反应处理
  • 高效性: 指算法运行效率高，及算法所消耗的时间短。算法时间复杂度就是指算法运行需要的时间，但是由于现在计算机一秒钟可以计算数亿次，所以我们不能使用秒来具体计算算法消耗的复杂度 ，由于相同配置的计算机进行一次的运算的时间是一定的，所以我们可以将基础算法的执行次数来衡量算法的效率 。因此将基本运算的 的执行次数作为时间复杂度的衡量标准
  • 低存储性：低储存是指算法所需要的储存空间低。算法占用的空间大小成为空间复杂度

除了前面3点的基本标准之外，我们对好算法的的评判标准就是高效率、低储存

1.3 时间复杂度

• 时间复杂度：算法运行需要的时间，一般将算法的执行次数作为时间复杂度的度量标准。但是不是每个算法都能直接计算算法次数。有些算法，如排序、查找、插入等算法，可以分为最好、最差、和平均情况分别求算法渐进复杂度，但是我们考察一个算法通常考查最坏的情况，而不考察最好的情况，最坏情况对衡量算法的好坏具有实际的意义
  

• 常见的时间复杂度有以下几类

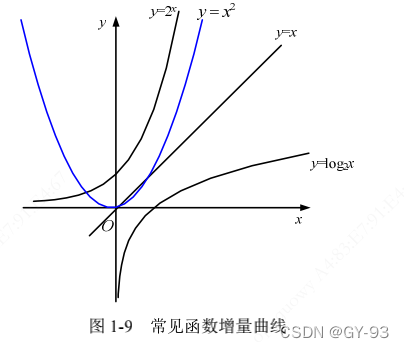
  • 常数阶：常数阶算法运行的次数是一个常数，如5,20,100.常数阶算法时间复杂度通常使用O(1)表示
  • 多项式阶：很多算法时间复杂度是多项式，通常使用O(n)、O（n^2）、O(n^3)等表示
  • 指数阶：指数阶时间复杂度运行效率极差，程序员往往像躲“恶魔”一样避开他。常见的有 （2^n）、O(n!)、O（n^n）等。使用这样的算法要慎重。例如：一个棋盘的麦子（一个古老的故事）的算法
  • 对数阶：对数阶时间复杂度运行效率高，常见的有O（log(n)）、O（nlogn）等
    

• 常见时间复杂度的曲线：

1.4 空间复杂度

• 空间复杂度：算法占用的空间大小，一般将算法的辅助空间作为衡量空间复杂度的标准，算法占用的储存空间包括：
  • 输入/输出数据
  • 算法本身
  • 额外需要的辅助空间
  • 输入输出数据占用空间可以忽略不计，算法本身占用的空间可以通过精简算法来缩减，但是这个压缩的量是很小的，可以忽略不计，而在运行时使用的辅助变量所占用的空间，及辅助空间是衡量算法空间复杂度的关键因素
    

2. 链表

2.1 线性表

2.1.1 线性表的介绍

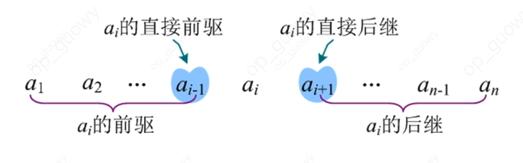
线性表是有n（你>= 0）个相同类型的数据元素组成的有限序列,它是最基本、最常用的一种线性结构。顾名思义，线性表就像一条线，不会分叉，每个元素。线性表有唯一的开始和结束，除了第一个元素外，每个元素都有唯一的直接前驱，除了最后一个元素，每个元素都有一个唯一的直接后继

• 线性表的前驱和后继：

2.1.2 线性表-顺序表

• 顺序表：是顺序储存方式，及逻辑上相邻的数据在计算机内的储存位置也是相邻的。顺序储存方式，元素存储是连续的，中间不允许有空。
• 优点：速定位第几个元素
• 缺点：插入、删除需要移动大量的元素
  

2.3 线性表-单向链表

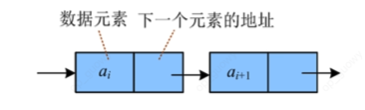
链表是线性表的存储方式，逻辑上相邻的数据在计算机内的存储位置不一定相邻，那么怎么表示逻辑上的相邻关系了？

• 单向链表的声明结构：

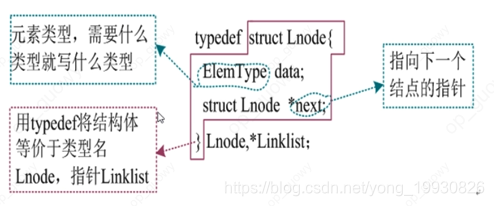
• 单向链表： 有些单向链表我们加上了头结点， 头结点是不存储数据的，是一个空的节点， 只是为了操作方便 什么情况下方便， 删除第一个节点的时候， 如果没有头结点，需要修改第一个节点的地址， 头指针需要指向第二个节点， 但是如果我有头结点， 删除第一个的时候，我们是不需要动头指针，直接跳过指向第二个节点就可以

• 第一个元素叫做首元节点，在存在头结点的时候，头指针会指向头结点

• 单向链表的最后一个节点的next域指向NULL ，就是后面没有数据了

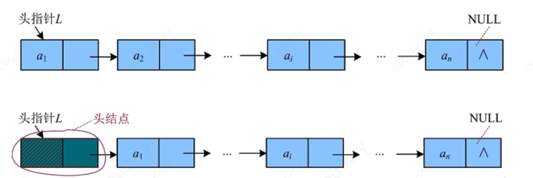
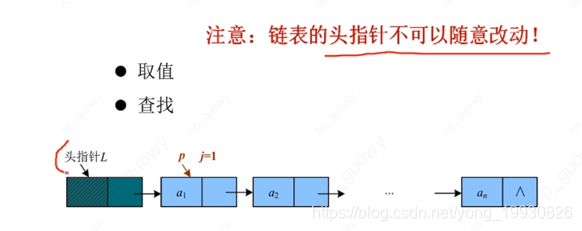
注意：链表的头指针是不可以随意移动的

2.2 单向链表实例练习

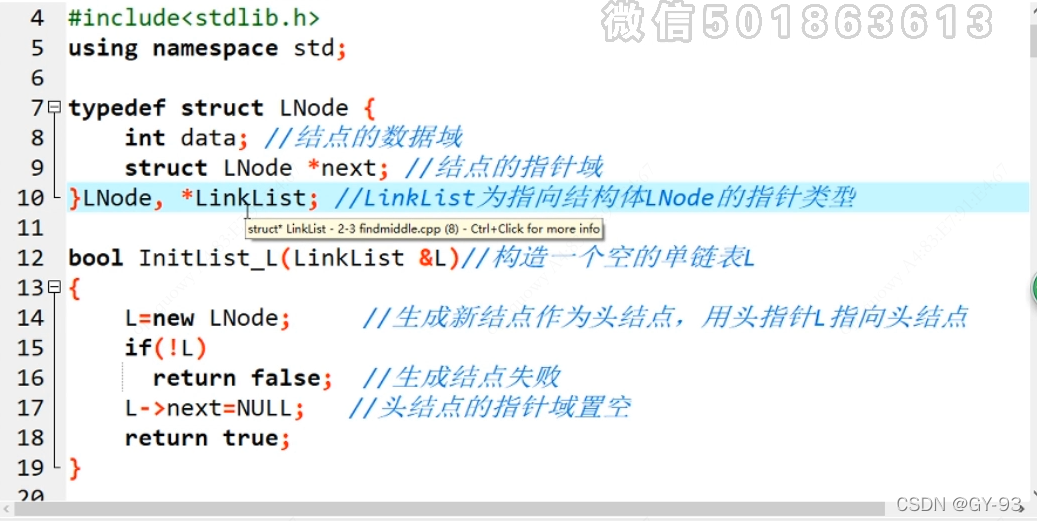
2.2.1 声明和创建一个空的单链表

• 初始化: 初始化 一个头指针 ，头指针的data域不存数据， next域指向NULL 初始化就成功了
  

//申明一个结构体
typedef struct LNode {
	int data; //结点数据域（这里你想储存什么类型就写什么类型， 这里以int类型为例）
	struct LNode *next; //结点的指针域
}LNode, *LinkList; //LinkList为指向结构体LNode的指针类型， LNode为对象 

//创建一个空的单链表L
bool InitList_L(LinkList &L)//构造一个空的单链表L，通常用大写的L来表示一个空链表的头指针
{
    L=new LNode;//生成新结点作为头结点，用头指针L指向头结点
	if(!L) //判断头结点创建是否创建成功
      return false;  //生成结点失败
	L->next=NULL;   //头结点的指针域置空
	return true;
}

2.2.2 创建链表

• 单向链表的创建分为两种，一种是头插法，一种是尾插法：
  • 头插法： 逆序建表， 每次都是从头指针的后面插入一个元素
  • 尾插法：顺序建表， 每次都是在链表的尾部插入一个元素
    

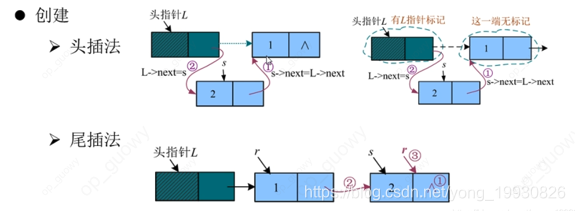
注意： 我们在修改指针标记的时候， 我们需要首先修改无标记的那一端， 然后在修改有指针标记的一端， 如果你想随便修该， 你可以声明一个零时变量，来记录无标记的一端，这里可能有很多人分不清楚声明时候用.属性名，什么时候用->属性名例：C语言中创建一个结构体， 变量对象（实例对象）调用属性时用. 例：变量名.属性名，指针反问属性时用-> 例：指针名->属性名

//使用头插法创建链表
void CreateList_H(LinkList &L)
{
	// 输入n个元素的值，建立到头结点的空连接L
	int n;
	LinkList s; //定义一个指针变量
	L=new LNode;
	L->next=NULL; //先创建一个带头结点的空链表
	cout <<"请输入元素个数n：" <<endl;
	cin>>n;
	cout <<"请依次输入n个元素：" <<endl;
	cout <<"头插法创建单链表" <<endl;
	while(n--)
    {
		s=new LNode; //生成新结点 s
		cin>>s->data; // 输入元素赋值给新结点的数据域
		s->next=L->next;// 把头结点指针域的值赋值给s的指针域
		L->next=s; //将新生成的结点s插入到头结点之后
	}
}

//尾插法创建链表
void CreateList_R(LinkList &L)
{
	// 输入n个元素的值，建立到头结点的空连接L
	int n;
	LinkList s, r;//定义两个指针变量
	L=new LNode;
	L->next=NULL; //先创建一个带头结点的空链表
	r=L; //尾指针r指向头结点, r相当增加的零时变量记录最后一个结点
	cout <<"请输入元素个数n：" <<endl;
	cin>>n;
	cout <<"请依次输入n个元素：" <<endl;
	cout <<"尾插法创建单链表" <<endl;
	while(n--)
    {
		s=new LNode;//生成新的结点
		cin>>s->data; // 输入元素值赋值给新结点的数据域
		s->next=NULL;//设置新结点的指针域为NULL
		r->next=s;//将新结点s插入到r结点之后
		r=s;//r指向新的结点s
	}
}

2.2.3 链表的查找

• 单向链表的取值和查找：

//单链表的取值： 查找链表L中第i个元素
bool GetElem_L(LinkList L, int i, int &e)
{
	//在带头结点的单链表L中查找第i个元素
	//用e记录L中第i个元素的值
	int j;
	LinkList p;//定义一个指针变量p
	p=L->next;//把单链表L的第一个结点赋值给p
	j=1; //j为计数器
	while (j<i && p) //顺链域向后扫描，直到p指向第i个元素或p为空
    {
		p=p->next; //p指向下一个结点
		j++; //计数器相应的加一
	}
	if (!p || j>i)
		return false; //p为空或i值不合法 则返回false
	e=p->data; //取第i个结点的数据域
	return true;
}

//按值查找
bool LocateElem_L(LinkList L, int e) 
{
	//在带头结点的链表L中查找值为e的元素
	LinkList p;
	p=L->next;
	while (p && p->data!=e)//顺链域向后扫描，直到p的数据域等于e或p为空
		p=p->next; //p指向下一个节点
	if(!p)
        return false; 
    return true;
}

2.2.4 链表的插入

• 插入：

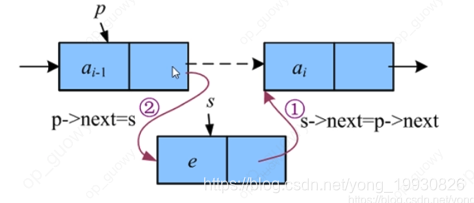
//单链表的插入
bool ListInsert_L(LinkList &L, int i, int e)
{
	//在带头结点的L链表中第i个位置插入值为e的新结点
	int j;
	LinkList p, s;//定义两个结点指针
	p=L;//把L头结点赋值给p
	j=0;
	while (p&&j<i-1) //查找第i-1个结点，P指向该节点
    {
		p=p->next;
		j++;
	}
	if (!p || j>i-1)
		return false;
	s=new LNode;     //创建一个新的结点
	s->data=e;       //把e赋值给新结点的数据域
	s->next=p->next; // 把p结点next域（也就是P+1位置的结点的地址值）赋值给s结点的next域，这样s结点就指向p+1个结点
	p->next=s;       // 把s结点的地址值赋值给p的next语 ，也就是p结点指向s结点 ，s结点指向原先的p+1位置的结点
	return true;
}

2.2.5 链表的删除

• 单向链表的删除

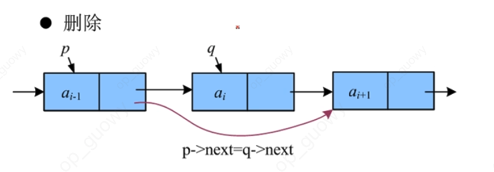
bool ListDelete_L(LinkList &L, int i) 
{
	//在带头结点的单向链表L中，删除第i个元素
	LinkList p, q; //定义两个结点指针
	int j;
	p=L;
	j=0;
	while((p->next)&&(j<i-1)) //判断p结点next是否为空，并且j<i-1
	{
		p=p->next;//把p指向下一个结点
		j++;
	}
	if (!(p->next)||(j>i-1))//如果p的next域为空，或则i不合法则返回false
		return false;
	q=p->next;        //找到需要删除的元素之后，把需要删除的结点赋值给q，这里p->next是我们当前需要删除的结点（临时保存被删除的结点的地址以备释放空间）
	p->next=q->next; //改变删除节点前驱的指针域
	delete q;        // 释放被删除结点的空间
	return true;
}

2.2.6 链表应用

题目：将两个有序（非递减）单链表La和Lb合并为一个新的有序（非递减）单链表。解题思路： 链表的合并不需要在创建空间，只需要穿针引线，把两个单链表中的结点，按非递减的顺序串联起来即可。注意：单链表的头指针是不可以移动的

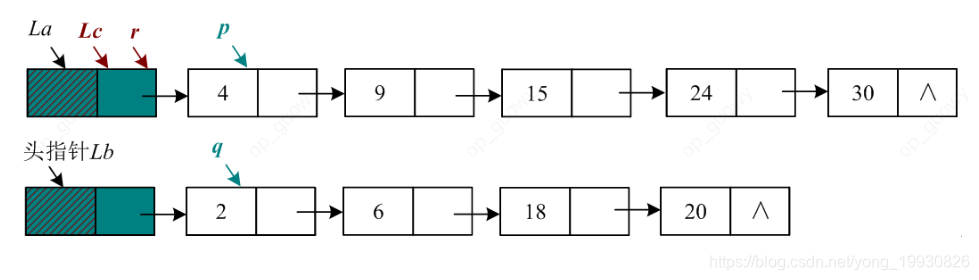
//链表的合并 把la和lb合并 lc表示合并后的链表
void mergelinklist(LinkList La, LinkList Lb, LinkList &Lc)
{
    LinkList p,q,r; //定义三个临时变量
    p=La->next; //p指向La的第一个元素
    q=Lb->next; //q指向Lb的第一个元素
    Lc=La;      //Lc指向La的头结点
    r=Lc;       //r指向Lc的尾部
    while(p&&q) // 判断只有当p和q都存在的时候吗，我们才有比较的必要
    {
        if(p->data<=q->data)
        {
        //如果p结点的值小于等于q结点值，那么把p指向的结点串起来
            r->next=p;
            r=p;
            p=p->next;//p往后移动一个结点 
        }
        else             
        {
        //如果p结点的值 大于 q结点的值， 那么就把q指向的结点串起来
            r->next=q;
            r=q;
            q=q->next; //q往后移动一个结点
        }
    }
    // 当不满足比较的情况时， 判断当前连个单链表那个是空， 然后把r结点（新链表的尾部）指向还剩下的链表的元素
    r->next=p?p:q;
    delete Lb;
}

题目：带有头结点的链表L，设计一个尽可能高效的算法求取L中的中间结点。
解题思路：这样的题型需要使用快慢指针来解决，一个快指针，一个慢指针，指针走两步慢指针走一步，当快指针走到结尾的时候，慢指针刚好走到中间

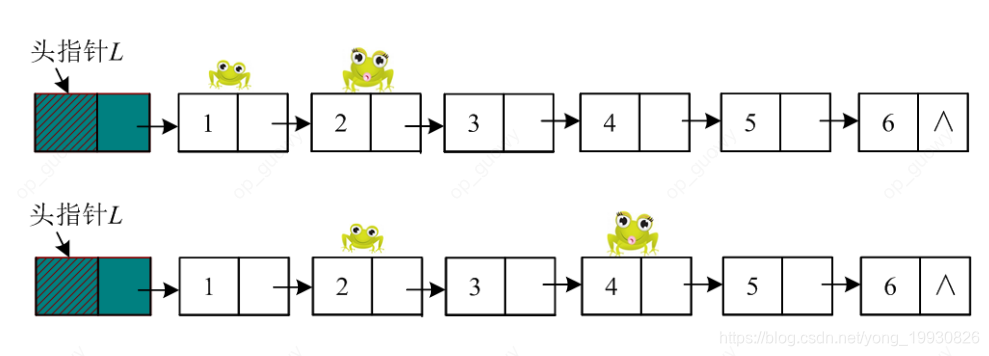
//高效的求链表L的中间结点
LinkList findmiddle(LinkList L)
{
	LinkList p,q;
    p=L; //p为快指针，初始指向L
    q=L; //q为慢指针，初始指向L
    while(p!=NULL&&p->next!=NULL) //判断P指针（快指针）存在，并且p的下一个结点也存在， 不然p->next->next 会出错
    {
        p=p->next->next;//p为快指针一次走两步
        q=q->next; //q为慢指针一次走一步
    }
    return q;//返回中间结点指针
}

2.2.7 示例作业

2.2.7.1 在单链表中查找倒数第k个结点

• 寻找单链表中的倒数第k个结点，最容易想到的遍历， 首先我们遍历一遍链表，求出链表的长度n，然后倒数第k个元素，也就是第n-k个结点， 那么接下来需要再遍历一遍得到结果， 但是该放大存在的问题是需要对链表遍历两边，第一遍求链表的长度， 第二遍用来查找n-k个元素。

//遍历查询单链表倒数第k个结点
void queryNodeFirst(LinkList L, int k) {
    //获取链表头指针后的第一个结点
    LinkList s = L->next;
    //链表的总长度
    int count = 0;
    while (s) { // n次
        count += 1;
        s = s->next;
    }
    
    //我们需要找的元素
    int currentCount = 0;
    LinkList r = L->next;
    while (r) { // n-k次
        if (currentCount == count - k) {
            printf("链表倒数第%d个元素=%d\n",k,r->data);
            //结束循环
            break;
        }
        
        currentCount += 1;
        r = r->next;
    }
}

• 上述方式还可以优化，第二种方法，从头到尾的方向，从链表的某个位置开始遍历，刚好遍历k个元素到达链表结尾，那么该元素就是我们要找的倒数第k个元素，根据这一性质，可以设计如下算法：从头节点开始，依次对链表的每一个节点元素进行这样的测试，遍历k个元素，查看是否到达链表尾，只到找到哪个倒数第k个元素。此种方法将对同一批元素进行反复多次的遍历，对于链表中的大部分元素而言，都要遍历K个元素，如果链表长度为n个的话，该算法的时间复杂度为O(kn)级，效率太低。

//从链表的中的某个元素循环， 循环k次之后，看是否到链表的末尾,如果到达链表末尾，则该结点是我们要找的结点， 否则重新循环
void queryNodeSecond(LinkList L, int k){
    LinkList s = L->next;
    LinkList r = L ->next;
    int loopCount = 0;
    while (s) { // k * n次
        loopCount += 1;
        if (loopCount == k) {
            if (r->next) {
                //不符合 从下一个元素开始循环
                loopCount = 0;
                s = s->next;
                r = s;
            } else {
                //循环k次 刚好到链表的末尾
                printf("链表的倒数第%d个元素=%d\n",k,s->data);
                break;
            }
            
        } else {
            r = r->next;
        }
    }
    // 时间复杂度 = O（k * n）
}

• 存在另外一个更高效的方式，只需要一次遍历即可查找到倒数第k个元素。由于单链表只能从头到尾依次访问链表的各个节点，因此，如果要找到链表的倒数第k个元素的话，也只能从头到尾进行遍历查找，在查找过程中，设置两个指针，让其中一个指针比另一个指针先前移k-1步，然后两个指针同时往前移动。循环直到线性的指针值为NULL时，另一个指针所指向的位置就是所要找到的位置。

// 链表中设置两个指针一个先移动，一个后移动， 快指针比慢指针先移动k-1步，然后在两个指针同时移动，循环知道快指针的指针值为NULL，另外一个指针所指向的位置就是所有找到的位置
void queryNodeThree(LinkList L, int k) {
    LinkList s,r;
    s = L->next;//先移动的指针
    r = L->next;//后移动的指针
    int setpCount = 0;
    while (s) { //n次
        if (setpCount > k-1) {
            //k指针已经移动k-1步，当再次移动的时候 r指针也需要移动一步
            r = r->next;
        }
        
        setpCount += 1;
        s = s->next;
    }
    
    printf("three:链表倒数第%d个元素是=%d\n",k,r->data);
    //时间复杂度 = O（n）
}

2.2.7.2 题目如下

用单链表保存m个整数，结点的结构为（data,next）,且|data|<=n(n为正整数)。现在要求我们设计一个时间复杂度尽量可能高效的算法，对于链表中的data的绝对值相等的结点，仅保留第一次出现的结点而删除其余绝对值相等的结点。

• 解题思路：
  1. 创建缓存链表中指定的数组
  2. 循环链表，判断每个结点的值的绝对值，是否在数组中存在， 如果存在，则执行删除该结点的操作， 不存在， 则把该结点的值的绝对值缓存到数组中
  3. 更换链表的指针，继续循环

2.3 双向链表

双向链表的结构：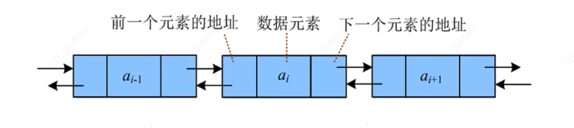

• 双向链表的插入：

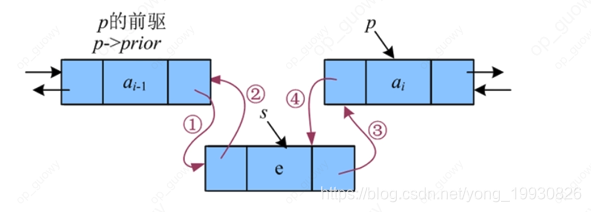
• 双向链表的删除：

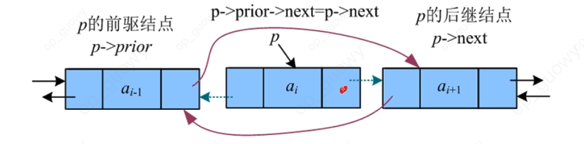
3. 栈和队列

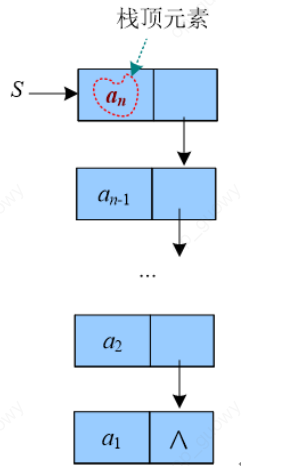
3.1 栈

后进先出（Last In First Out，LIFO）的线性序列，称为“栈”。栈也是一种线性表，只不过它是操作受限的线性表，只能在一端进出操作。进出的一端称为栈顶（top），另一端称为栈底（base）。栈可以用顺序存储，也可以用链式存储，分别称为顺序栈和链栈

3.1.1 顺序栈

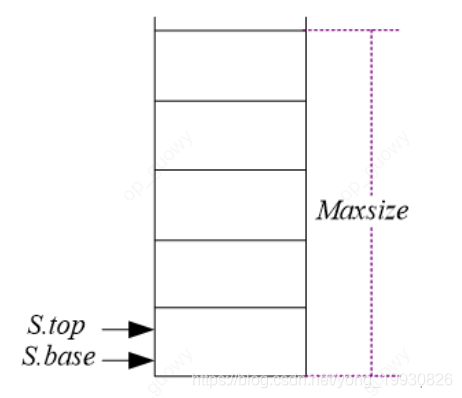
顺序栈： 需要两个指针base指向栈底，top指向栈顶：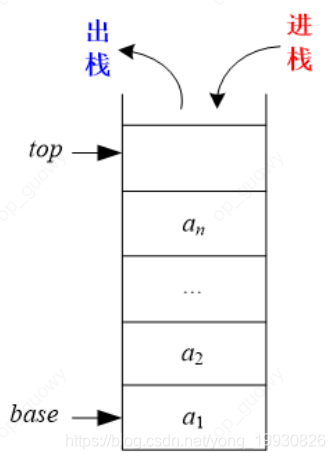

顺序栈是一组连续的空间 , 当top=base表示栈是空的，每添加一个元素时，top指针就+1，取数据的时候，只需要top指针-1

• 顺序栈动态分配（使用new关键字实现动态分配内存）：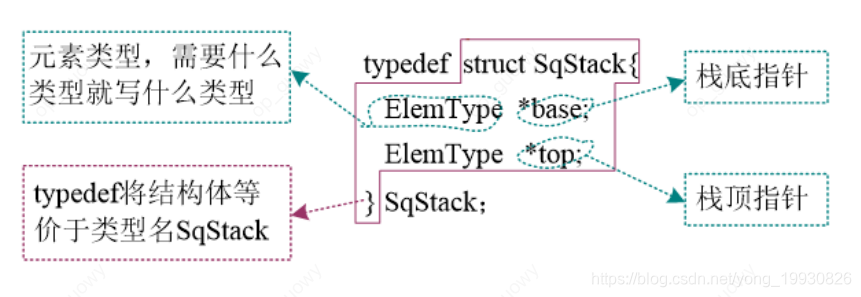

顺序栈静态分配（直接创建一个固定长度的一维数组）：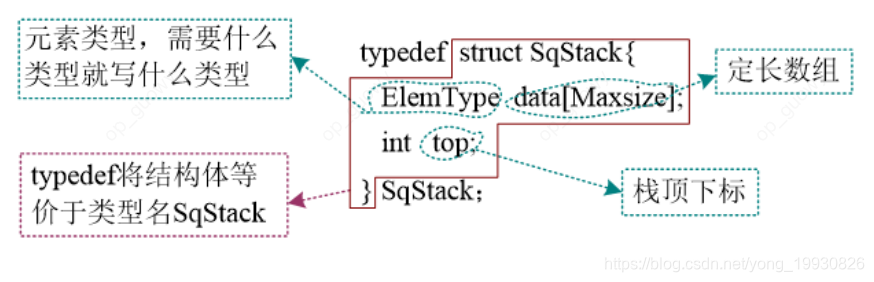

3.1.2 栈的初始化

c++中可以使用& 引用参数， 但是C语言是不可以使用的

#define Maxsize 100  //预先分配空间，这个数值根据实际需要预估确定；一般比实际需要大一些
//申明一个栈类型
typedef struct SqStack {
	int *base; //栈底指针
	int *top; //栈顶指针
}SqStack;

//初始化一个空栈
bool InitStack(SqStack &S) //构造一个空栈S
{
	S.base = new int[Maxsize];//为顺序栈分配一个最大容量为Maxsize的空间
	if (!S.base)    //空间分配失败
		return false;
	S.top=S.base;  //top初始为base，空栈 
	return true;
}

3.1.3 栈的插入

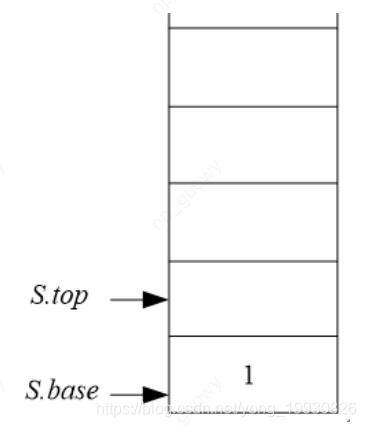
入栈：当往栈内插入一个元素时，需要判断是不是满栈，如果是满栈则无法插入元素，s.top栈的顶部指针会向上移动一个位置

bool Push(SqStack &S, int e) // 插入元素e为新的栈顶元素
{
	if (S.top-S.base == Maxsize) //栈满
		return false;
	*(S.top++) = e; //元素e压入栈顶，然后栈顶指针加1，等价于*S.top=e; S.top++;
	return true;
}

3.1.4 栈的删除

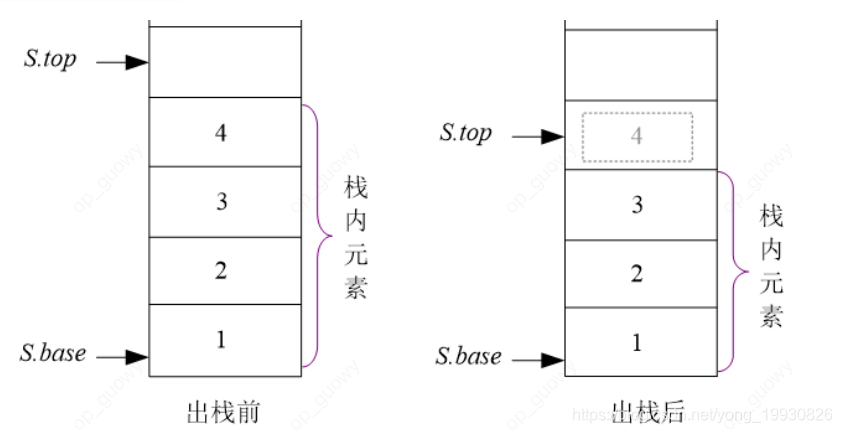
出栈：首先需要判断栈是否是空栈，如果是空栈，则没有元素可以出栈， 如果不是空栈，出栈一个元素，s.top指针向下移动一个位置。注意： 出栈之后，栈内的元素在下一个进栈元素覆盖之前，是还保存着原来的值的，并没有消失

bool Pop(SqStack &S, int &e) //删除S的栈顶元素，暂存在变量e中
{
	if (S.base == S.top) //栈空
		return false;
	e = *(--S.top); //栈顶指针减1，将栈顶元素赋给e 等价于： e = *(S.top-1); --S.top;
	return true;
}

如何获取栈顶的元素：

int GetTop(SqStack S) //返回S的栈顶元素，栈顶指针不变
{
	if (S.top != S.base)  //栈非空
		return *(S.top - 1); //返回栈顶元素的值，栈顶指针不变
    else
        return -1;
}

• 测试：

//测试栈的方法
//测试栈的方法
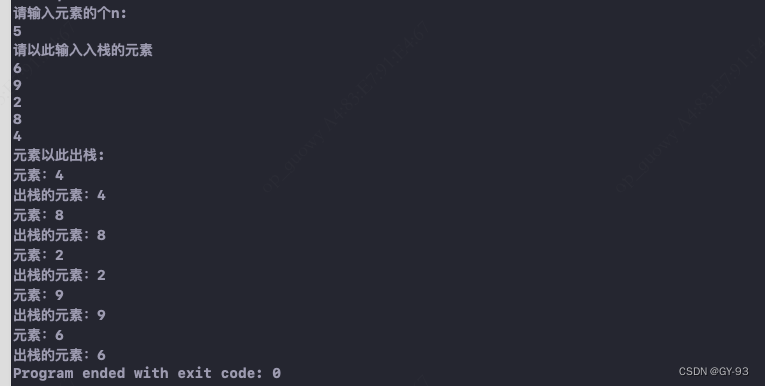
void testStackDemo(){
    //初始化一个顺序栈S
    SqSatck S;
    //需要入栈的元素的个数
    int n;
    //初始化一个空栈
    bool result = InitStack(S);
    if (result) {//初始化栈成功
        std::cout << "请输入元素的个n:" << std::endl;
        std::cin >> n;
        std::cout << "请以此输入入栈的元素" << std::endl;
        while (n--) {
            int x;
            std::cin >> x;
            pushStack(S, x);
        }
        
        std::cout << "元素依次出栈:" << std::endl;
        while (S.top != S.base) {
            std::cout << "元素：" << getStakTopElement(S) << std::endl;
            popStack(S);
        }
    }
}

3.1.5 链栈

链栈只需要一个指针，如何判断栈底，判断的结点next域是否是NULL，如果是NULL则是栈底，其操 跟链表操作类似：

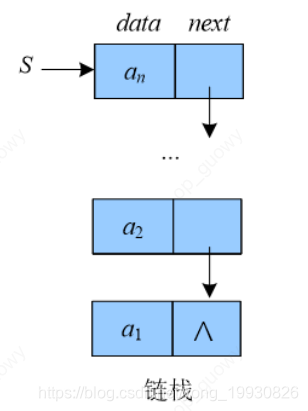
链栈其本质上就是一个单链表，链栈是不需要头结点的

链栈的插入和删除元素和链表的插入、删除一样：

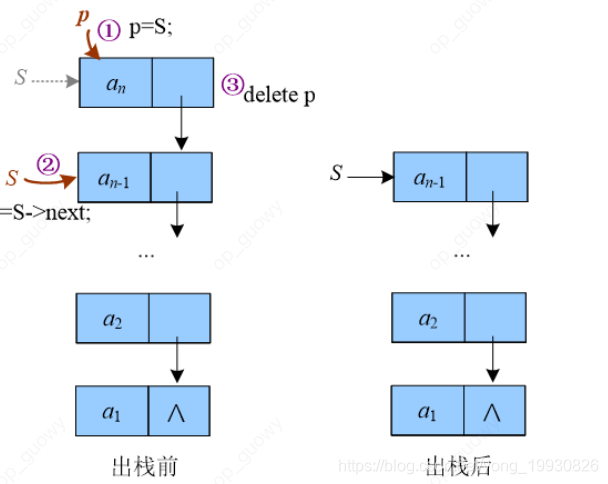
使用p变量记录结点的原因是因为要释放掉出栈的空间，动态生成的结点如果不释放，可能造成内存泄漏的问题

• 取栈顶元素，直接是S->data

3.2 队列

3.2.1 队列概念

• 先进先出（First In First Out，FIFO）的线性序列，称为“队列”。队列也是一种线性表，只不过它是操作受限的线性表，只能在两端操作：一端进，一端出。进的一端称为队尾（rear），出的一端称为队头（front）。队列可以用顺序存储，也可以用链式存储(只可以一端进，一端出，不可以从中间插入删除)

• 队列的顺序储存形式，可以用一段连续的空间存储数据元素，用两个整型变量记录对头和队尾元素的下标。
  

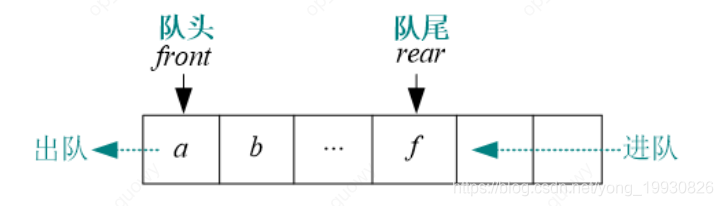
• 顺序队列动态分配：

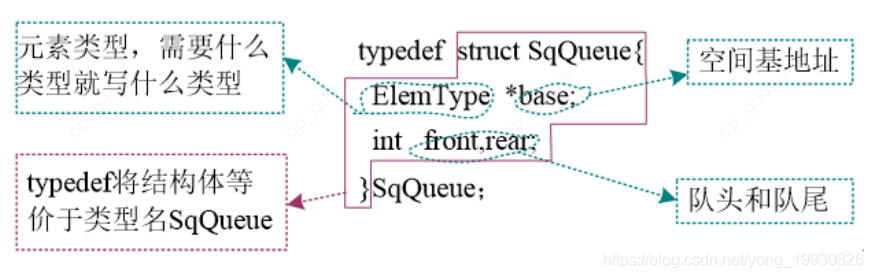
我们可以把队列看做一个数组来用，base指向数组的首地址，front和rear表示下标

• 静态分配：

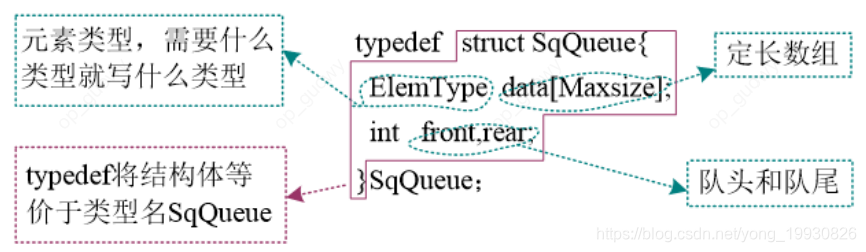
3.2.2 对列初始化

typedef  struct SqQueue{
  int *base; //基地址
  int front,rear; //头指针,尾指针
}SqQueue;

//循环队列的初始化
bool InitQueue(SqQueue &Q)//注意使用引用参数，否则出了函数，其改变无效
{
	Q.base=new int[Maxsize];//分配空间
	if(!Q.base) return false;
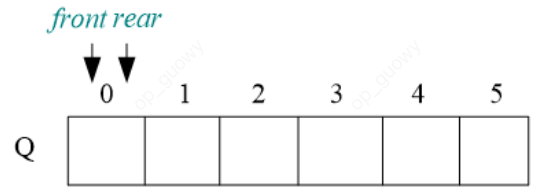
	Q.front=Q.rear=0; //头指针和尾指针置为零，队列为空
	return true;
}

3.2.3 入队和出队

• 入队：front表示队头，rear表示队尾，入队操作，

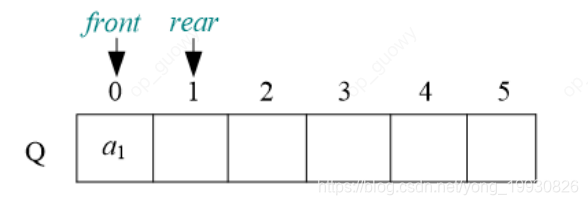
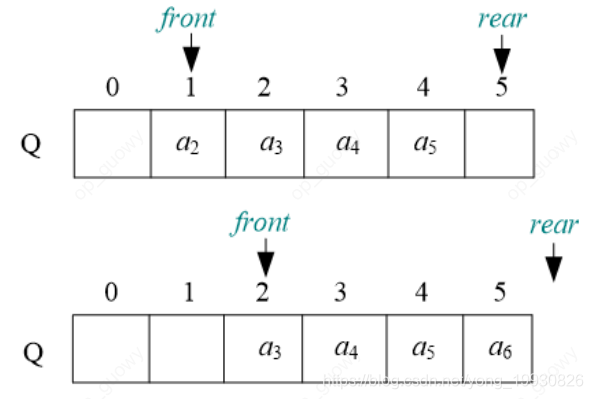
假溢出，队列可以一边入队，一边出队，所以为了防止我们出现假溢出的情况，一般我们使用循环队列的方式

3.2.4 循环队列

有时候当我们一直添加元素之后，队列后面空间满了，但是前面有出队，这时候我们会发生假溢出的现象，这个时候其实队列并没有满， 所以当我们再次添加元素的时候，我们会把元素添加到前面，这样就形成了循环队列

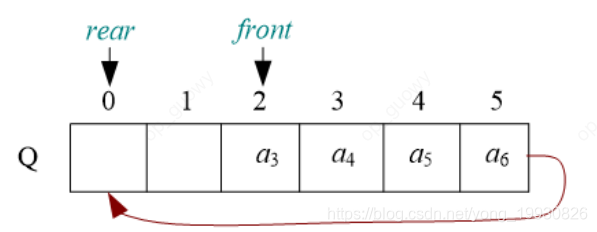
• 队空：当队头下标和队尾下标相等的时候我们认为这个时候队列是空的
  

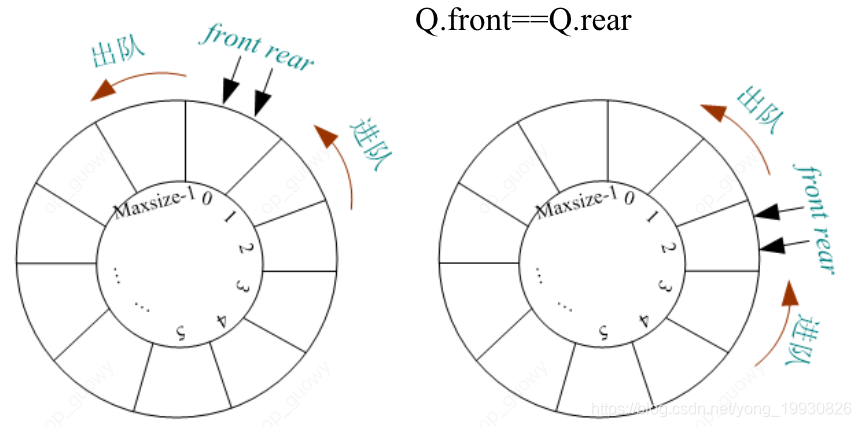
• 队满：当rear+1 对MaxSize取余等于队列的front的时候我们认为队列此时是满了，这时候rear下标此时是没有储存元素的，所以我们说队满，其实我们是浪费一个空间用来判断队满
  

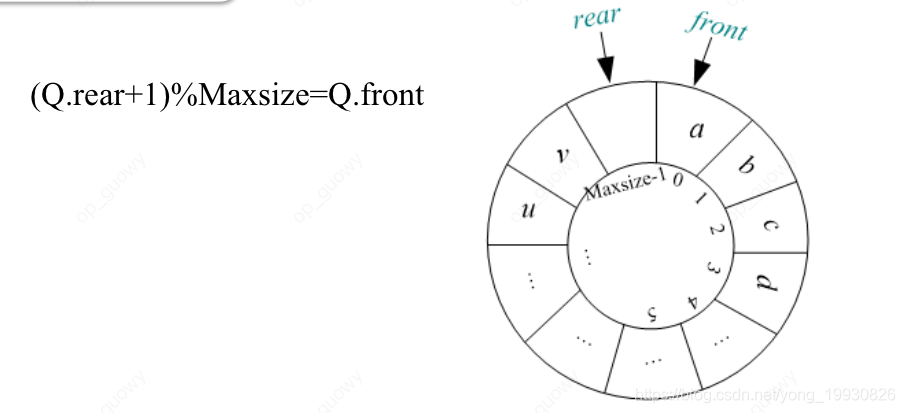
3.2.5 循环队列的出队和入队

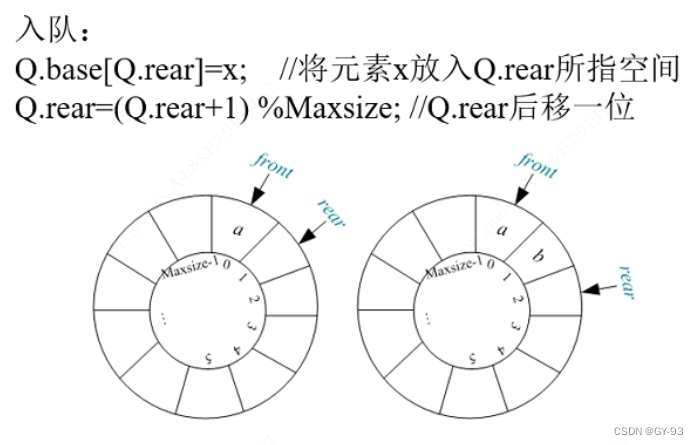
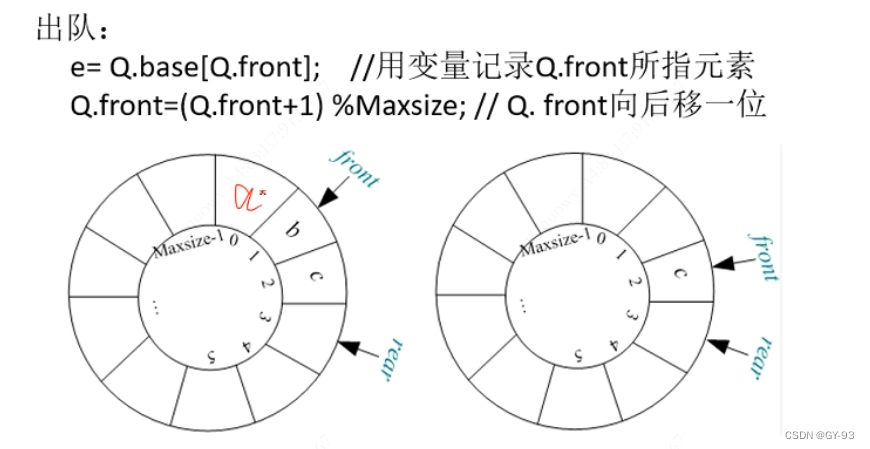
• 出队和入队 rear和front的下标都是+1 像后移
• 入队:

//循环队列的入队
bool EnQueue(SqQueue &Q,int e)//将元素e放入Q的队尾
{
	if((Q.rear+1)%Maxsize==Q.front) //尾指针后移一位等于头指针，表明队满
		return false;
	Q.base[Q.rear]=e; //新元素插入队尾
	Q.rear=(Q.rear+1)%Maxsize; //队尾指针加1
	return true;
}

• 出队：

//循环队列的出队
bool DeQueue(SqQueue &Q, int &e) //删除Q的队头元素，用e返回其值
{
	if (Q.front==Q.rear)
		return false; //队空
	e=Q.base[Q.front]; //保存队头元素
	Q.front=(Q.front+1)%Maxsize; //队头指针加1
	return true;
}

3.2.6 循环队列的头元素和队列长度

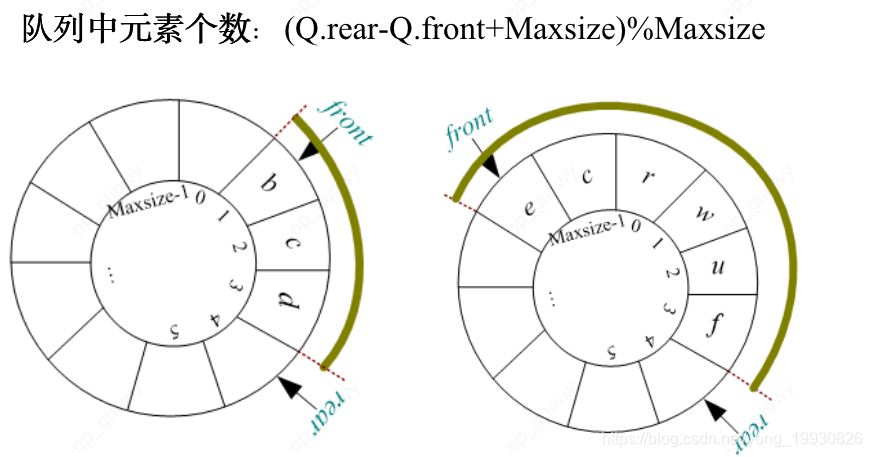
//取循环队列的队头元素
int GetHead(SqQueue Q)//返回Q的队头元素，不修改队头指针
{
	if (Q.front!=Q.rear) //队列非空
		return Q.base[Q.front];
    return -1;
}
//循环队列的长度
int QueueLength(SqQueue Q)
{
	return (Q.rear-Q.front+Maxsize)%Maxsize;
}

• +Maxsize：是防止Q.rear-Q.front计算为负数，加上Maxsize之后得到一个正确的队列长度，然后再进行取余计算得到还是队列长度
• %Maxsize：防止Q.rear-Q.front为正数，然后再加上Maxsize在对Maxsize取余操作，得到正确的队列长度

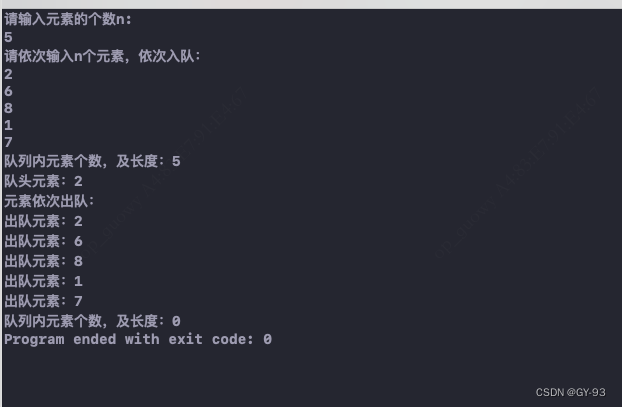
测试示例：

void testQueueDemo() {
    SqQueue S;
    int n,x;
    bool result = initQueue(S);
    if (result) {
        std::cout<<"请输入元素的个数n:"<<std::endl;
        std::cin>>n;
        std::cout<<"请依次输入n个元素，依次入队："<<std::endl;
        while (n--) {
            std::cin>>x;
            //入队
            enterQueue(S, x);
        }
        
        std::cout<<"队列内元素个数，及长度：" << getQueueElementCount(S) << std::endl;
        std::cout<<"队头元素："<< getQueueHeadElement(S)<<std::endl;
        std::cout<<"元素依次出队："<< std::endl;
        while (true) { //如果栈不空，则依次出栈
            if (!removeQqueue(S)) {
                break;
            }
        }
        
        std::cout<<"队列内元素个数，及长度：" << getQueueElementCount(S) << std::endl;
    }
}

3.2.7 链队

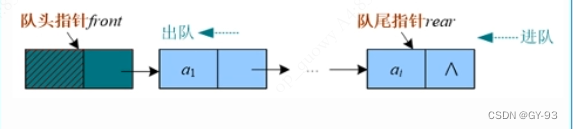
注意：链队是需要有头结点，因为我们经常需要删除元素

4. 二叉树

4.1 树的基础介绍

• 树（tree）是n（n>= 0）个结点的有限集合，当n=0时，为空树；，当n>0时，为非空树。任意一个非空树满足：
  • 有且仅有一个称之为根的结点
  • 除跟结点以为的其余结点为m（m>=0）个互不相交的有限集合T1，T2…Tm,其中每一个集合本身又是一颗树，并且称为根的子树（SubTree）

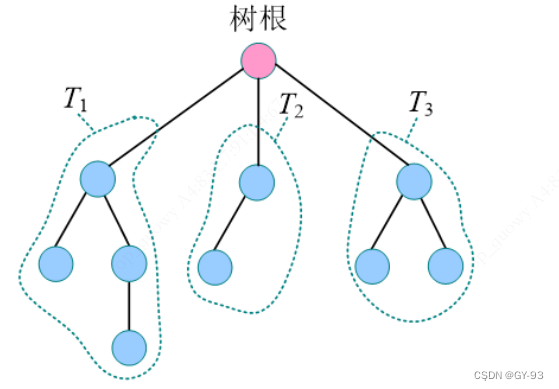
• 结点：结点包含数据元素及若干指向子树的分支信息
• 结点的度：结点拥有的子树个数
• 树的度：树中结点的最大度数
• 终端结点：度为0的结点，又称为叶子
• 分支结点：度大于0的结点，除了叶子都是分支结点
• 内部结点：除了树根河叶子都是内部结点
• 结点的层次：从根到该结点的层数（根结点为第一层）
• 树的深度（或高度）：指所有结点中最大的层数。

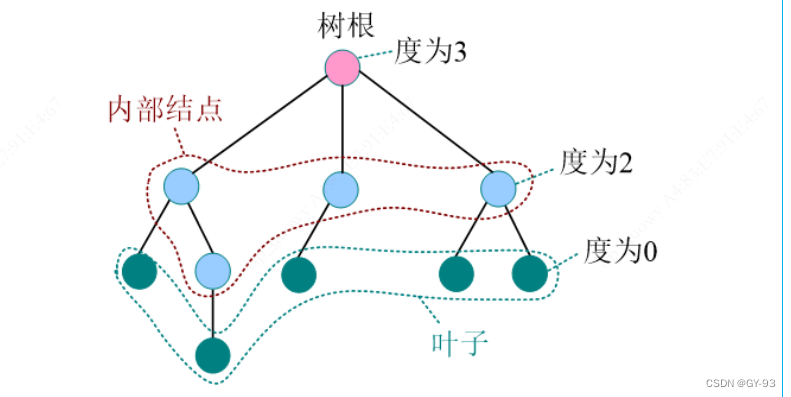
• 路径：书中两个结点之间的所经过的结点序列
• 路径长度：两节点之间路径上经过的边数
• 双亲、孩子：结点的子树的根成为该结点的孩子
• 兄弟：双亲相同的结点互称兄弟
• 堂兄弟：双亲是兄弟的结点互称堂兄弟
• 祖先：即从该节点到树根经过的所有结点，称为该节点的祖先
• 子孙：结点的子树中的所有结点都称为该节点的子孙
• 有序树：结点个子树从左至右有序，不能互换位置
• 无序树：结点各子树可互换位置
• 深林：由m（m>=0）棵不相交的树组成的集合。

4.2 树的存储结构

采用顺序储存和链式存储两种形式

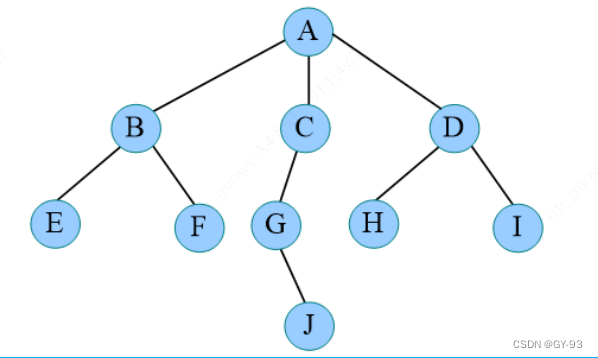
• 顺序储存
  

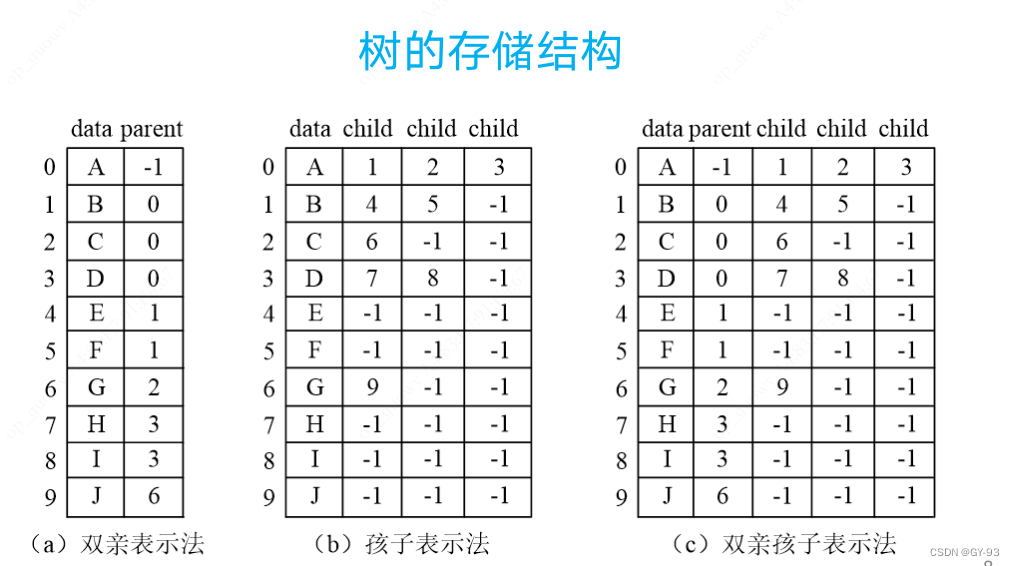
• 链式存储
  

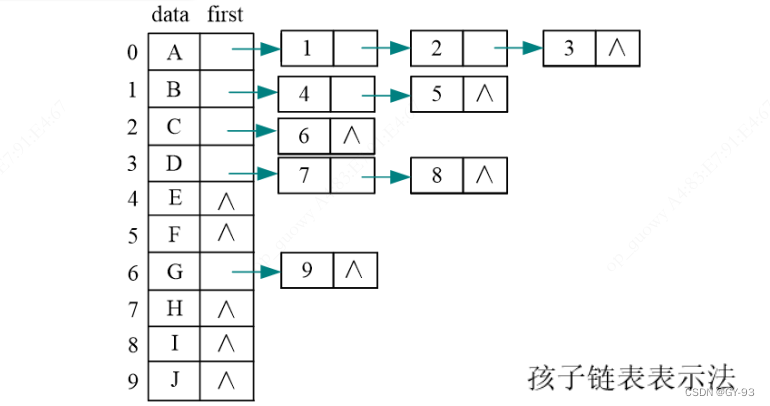
4.3 二叉树介绍

• 二叉树（Binary Tree）是n（n>=0）个结点所构成的集合，它或为空树（n= 0）；或为非空树。对于非空树T满足

  • 有且仅有一个称为根的结点
  • 除根结点以外，其余结点分为两个互不相交的子集T1和T2，分别称为T的左子树和右子树，且T1和T2本身都是二叉树

• 二叉树有如下性质：

  • 在二叉树的第i层上至多有2^i-1个结点。
  • 深度为k的二叉树至多有2^k-1个结点。
  • 对于任何一棵二叉树，若叶子数为n0度为2的节点数为n2，则n0=n2+1
    • 满二叉树：一棵深度为k且有2^k-1个结点的二叉树
    • 完全二叉树：除了最后一层，每一层都是满的（达到最大节点数），最后一层结点是从左向右出现的
  • 具有n个结点的完全二叉树的深度必为【log2n】+ 1
  • 对于完全二叉树，若从上至下、从左至右编号，则编号为i的结点，其左孩子编号必为2i，其右孩子编号必为2i+1;其双亲的编号必为i/2.
    

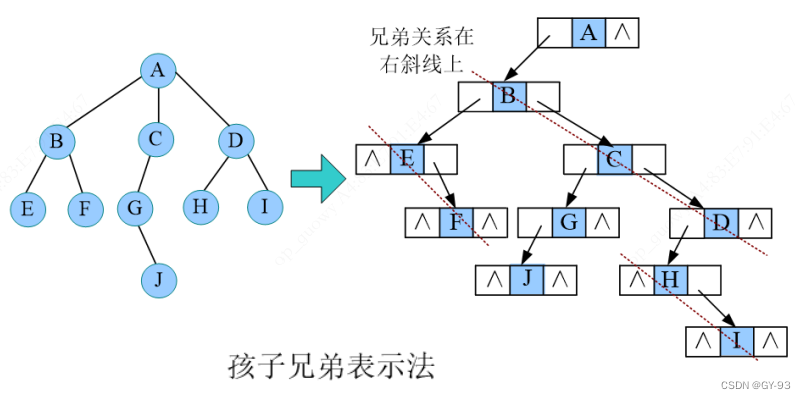
• 树转换成二叉树，孩子兄弟表示法的秘诀：长子当做左孩子，兄弟关系向友斜。
  

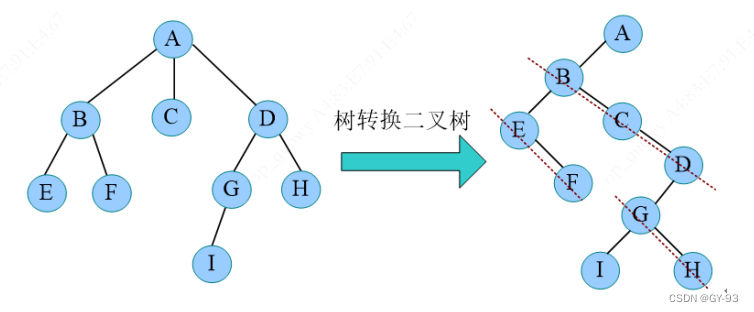
• 二叉树还原树
  

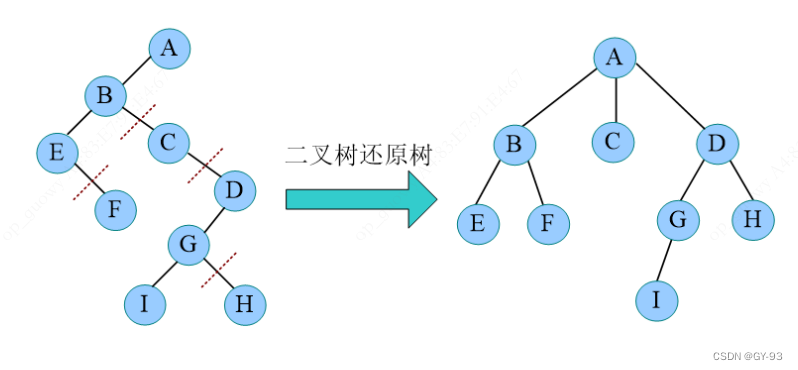
• 森林转换二叉树：
  

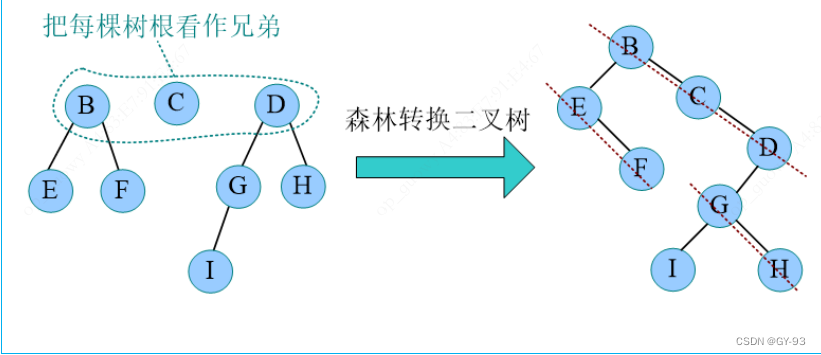
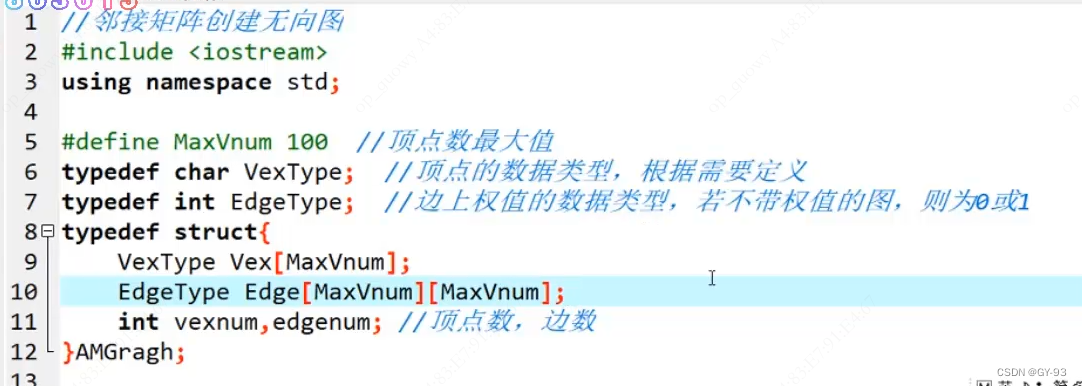
4.4 二叉树的存储

• 顺序储存，补0操作，该方法除非是一个完全的二叉树，我们可以使用该方法储存， 不然 那就需要补0的操作太多了
  
  

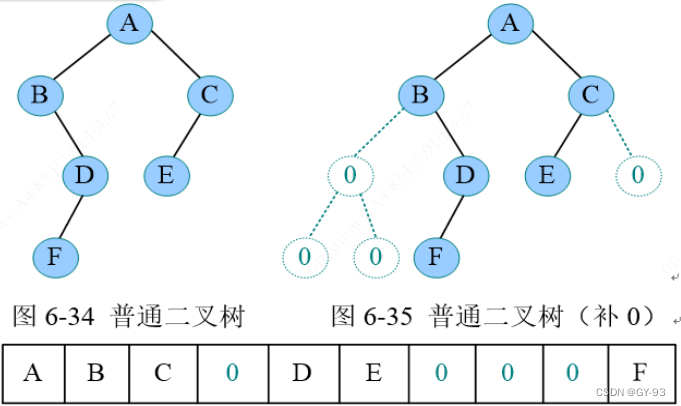
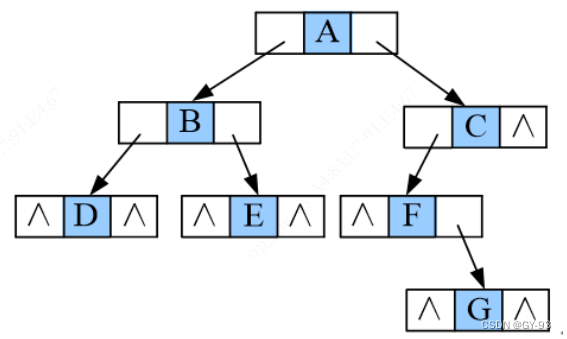
上述方法其实也可以使用两个数组来储存， 一个数组存左结点， 一个数组存右结点

4.5 二叉树的创建

• 补空法是指如果左子树或右子树为空时，则用特殊字符补空，如#。然后按照先序遍历的顺序，得到先序遍历序列，根据该序列递归创建二叉树。
• 算法步骤：
  • 输入补空后的二叉树先序遍历序列
  • 如果ch==’#‘，T=NULL；否则创建一个新结点T，令T->data= ch，然后递归创建T的左子树；递归创建T的右子树。

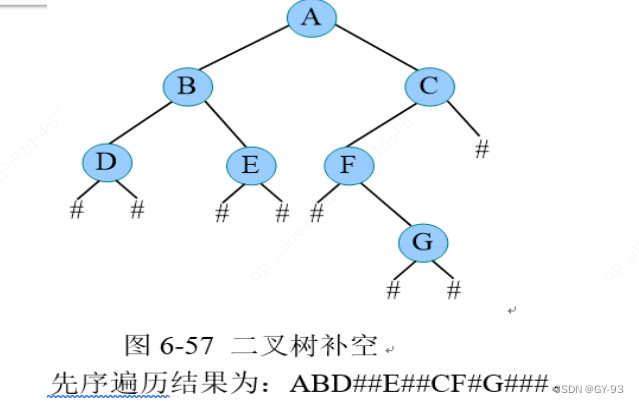
// 定义二叉树的存储结构
typedef struct Bnode {
    char data;//定义数据域
    struct Bnode *child,*rchild;//定义连个指针，表示左孩子 和 右孩子
}Bnode, *Btree;

//创建二叉树
void createTree(Btree &T) {
    //按先序顺序输入二叉树中结点的值（一个字符），创建二叉链表表示的二叉树T
    char ch;
    //从控制台输入
    std::cin>>ch;
    if (ch == '#') {
        T = NULL;//递归结束传递空树
    } else {
        T = new Bnode; //创建一个新的结点
        T->data = ch;
        //递归创建左子树
        createTree(T->child);
        //递归创建右子树
        createTree(T->rchild);
    }
}

4.6 二叉树的遍历

按照根的访问顺序不同，根在前面称为先序遍历（DLR），根在中间称为中序遍历（LDR），根在后面称为后续遍历（LRD）

4.6.1 先序遍历

先序遍历是指先访问根，然后先序遍历左子树，在先序遍历右子树，即DLR

• 算法步骤
  • 如果二叉树为空，则空操作，否则
  • 访问根节点
  • 先序遍历左子树
  • 先序遍历右子树
  • 注意：先序遍历，访问根，先序遍历左子树，左子树为空或已经遍历才可以遍历右子树

void preorder(Btree T) {
    //如果是空树，则直接返回
    if (!T) {
        return;
    }
    
    //先序遍历二叉树， 首先访问根， 在递归访问左子树（遍历左子树）， 在递归访问右子树（遍历右子树）
    std::cout << T->data;
    preorder(T->child);
    preorder(T->rchild);
}

4.6.2 中序遍历

中序遍历是指中序遍历左子树，然后再访问根，在中序遍历右子树，即LDR
算法步骤：

• 中序遍历左子树
• 访问根结点
• 中序遍历右子树
• 注意：中序遍历左子树，左子树为空或已遍历才可以访问根，中序遍历右子树

void inorder(Btree T) {
    // 如果是空树，则直接返回
    if (!T) {
        return;
    }
    //中序遍历: 先访问左子树（递归遍历所有左子树），在访问根， 在遍历右子树（递归遍历所有的右子树）
    //递归访问左子树
    inorder(T->child);
    //访问根
    std::cout<<T->data;
    //递归访问右子树
    inorder(T->rchild);
}

4.6.3 后续遍历

后序遍历是指后续遍历左子树，后续遍历右子树，然后访问根，即LRD
算法步骤：

• 如果二叉树为空，则空操作，否则
• 后续遍历左子树
• 后续遍历右子树
• 访问根结点
• 注意:后续遍历左子树，后续遍历右子树，左子树、右子树为空或已遍历才可以访问根

void postorder(Btree T) {
    //如果是空树 ，则直接返回
    if(!T) {
        return;
    }
    
    //后续遍历：先反问左子树（递归遍历所有左子树），在访问右子树（递归遍历所有右子树）， 最后访问根
    postorder(T->child);
    postorder(T->rchild);
    std::cout<<T->data;
}

4.6.4 层次遍历

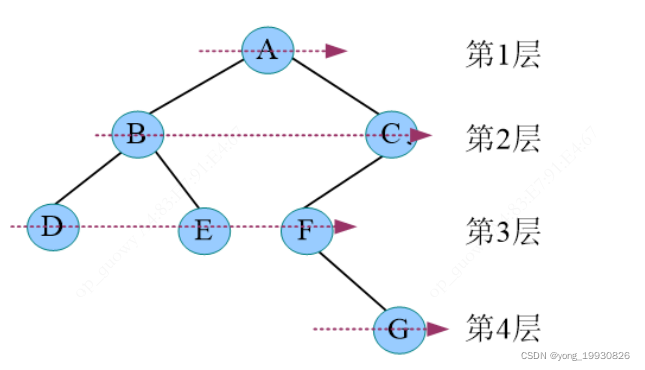
//使用队列实现层序遍历
void leveltraverse(Btree T) {
    Btree p;
    if (!T) {
        return;
    }
    
    std::queue<Btree> Q;//声明一个普通队列（先进先出），队列中存放都是指针类型
    Q.push(T);//入栈，根
    while (!Q.empty()) { //判断队列是否为空
        p = Q.front();//获取队头元素作为当前的扩展结点livenode
        Q.pop();//队头元素出队
        std::cout<<p->data;
        if (p->child) {//左孩子入队
            Q.push(p->child);
        }
        
        if (p->rchild) {//右孩子入队
            Q.push(p->rchild);
        }
    }
}

测试代码：

void testTreeDemo() {
    Btree T;
    std::cout<<"按先序次序输入二叉树中结点的值（孩子结点为空时输入#），创建一个二叉树"<<std::endl;
    createTree(T);//创建二叉树
    std::cout<<"二叉树的先序遍历结果："<<std::endl;
    preorder(T);
    std::cout<<"\n二叉树的中序遍历结果："<<std::endl;
    inorder(T);
    std::cout<<"\n二叉树的后序遍历结果："<<std::endl;
    postorder(T);
    std::cout<<"\n二叉树的层序遍历结果:"<<std::endl;
    leveltraverse(T);
    std::cout<<"\n"<<std::endl;
}

4.6.5 二叉树的还原

示例：一直一棵二叉树的先序遍历ABDFECFG和中序遍历DBEAFGC，画出这课二叉树。

• 算法步骤：
  • 先序遍历的第一个字符为根，
  • 中序序列中，以根为中心划分左右子树
  • 还原左右子树
    
    

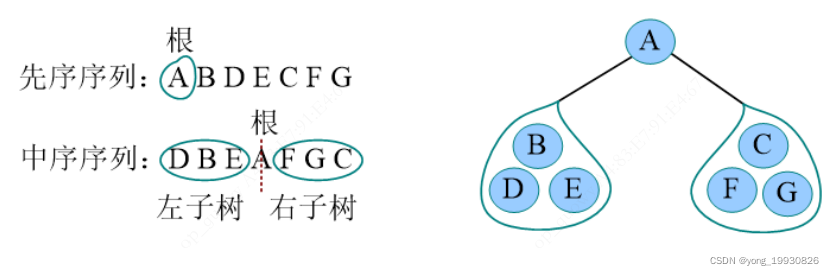
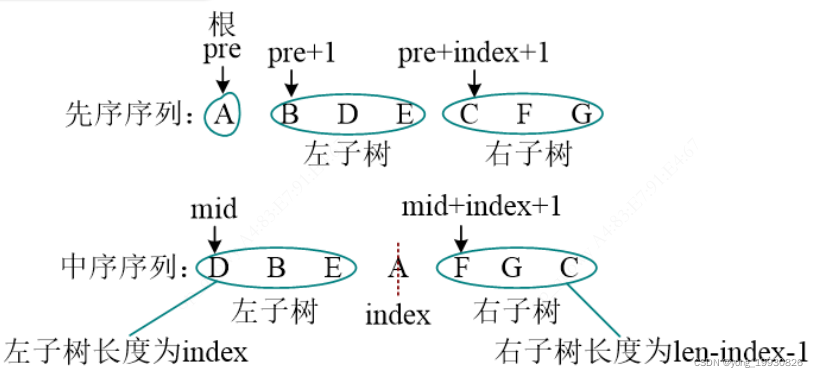
// 先序和中序还原二叉树
Btree pre_mid_creatBtree(char *pre, char *mid, int len){
    /**
     * 先序和中序还原二叉树
     * 1、先序的第一个结点是二叉树的根， 所以需要找到先序的第一个元素
     * 2、在中序中找到的根的结点为该节点的左子树，右边的为右子树
     * 3、递归创建左子树， 递归创建右子树
     */
    
    if (len == 0) {
        return NULL; //如果给的字符串长度为0 则为空树
    }
    
    char ch=pre[0];//获取先序字符串的第一个元素 就是二叉树的根
    int index = 0;
    //循环中序字符串，找到中序中的根字符串
    while (mid[index] != ch) { //找到 二叉树 根之后 结束循环
        index++;
    }
    
    Btree T = new Bnode;//创建根节点
    T->data = ch;
    //创建左子树
    T->child = pre_mid_creatBtree(pre+1, mid, index);
    T->rchild = pre_mid_creatBtree(pre+index+1, mid+index+1, len-index-1);
    
    return T;
}

中序和后续还原二叉树：

// 后续和中序还原二叉树
Btree pro_mid_createBtree(char *last, char *mid, int len) {
    if (len == 0) {
        return NULL; //如果给的字符串长度为0 则为空树
    }
    
    char ch=last[len-1];//获取先序字符串的第一个元素 就是二叉树的根
    int index = 0;
    //循环中序字符串，找到中序中的根字符串
    while (mid[index] != ch) { //找到 二叉树 根之后 结束循环
        index++;
    }
    
    Btree T = new Bnode;//创建根节点
    T->data = ch;
    //创建左子树
    T->child = pro_mid_createBtree(last, mid, index);//先序指针向前移动1
    T->rchild = pro_mid_createBtree(last+index, mid+index+1, len-index-1);
    
    return T;
}

5 图

5.1 图的基础介绍

线性表中，数据元素是一对一的关系，除了第一个和最后元素外，每个元素都有唯一的前驱和后继。树形结构中，数据元素是一对多的关系，除了根之外，没个结点都有唯一的双亲结点，可以有多个孩子。图形结构中是多对多的关系，任何两个数据元素都有可能有关系，每个结点可以有多个前驱和后继。

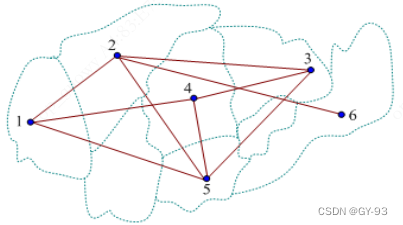
图通常用一个二元数组表示：G<V,E>,V表示顶点集，E表示边集。|V|表示顶点集中元素的个数，即顶点数，也称为G的阶，例如n阶图，表示途中有n个顶点。|E|表示边集中元素的个数，即边数。

注意：顶点集V和边集E均为有限集合，其中E可以为空集，V不可以为空集，也就是说一个图至少有一个顶点。线性表和树可以为空表和空树，图不可以为空图

5.2 图的种类

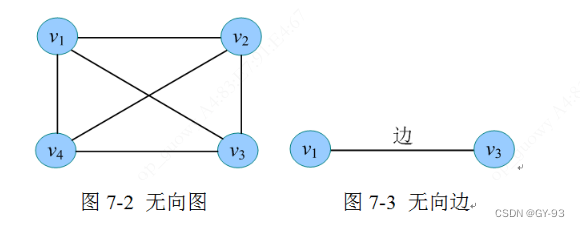
若图G中每条边都是没有方向的，则称为无向图。如上图所示，每条边都是两个顶点组成成的无序对，例如顶点v1和顶点v3之间的边，记为（v1，v3）或（v3，v1）

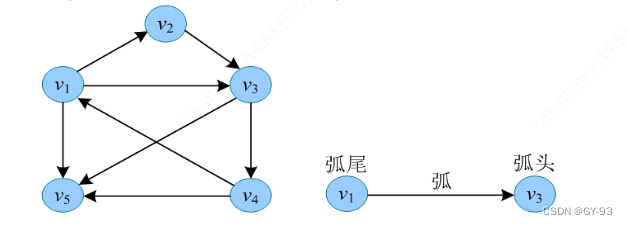
若图G中每条边都是有方向的，则称为有向图,如上图所示，有向边也称为弧，每条弧都是有两个顶点组成的有序对，例如从顶点v1到顶点v3的弧，记为<v1,v3>,v1称为弧尾，v3被称为弧头。
注意：尖括号<Vi, Vj>表示有序对，圆弧括号（Vi，Vj）表示无序对

既不含平行边也不含自环的图称为简单图， 如上述介绍的 两幅图均是简单图。

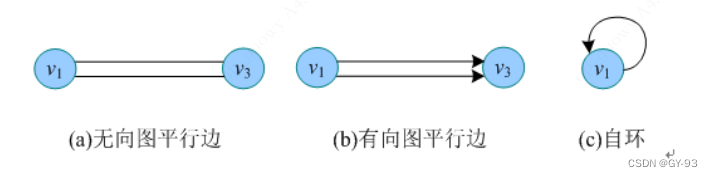
无向图中，关联一对顶点的无向边多余一条，则称这些边为平行边，平行边的条数称为重数。如山上图中（a）图所示。

有向图中，关联一对顶点的有向边多余一条，并且这些边的始点和终点相同（方向一致），则称这些边为平行边，如上图中（b)所示

自环是指一条边关联的两个顶点为同一顶点，也就是说自己到自己的一条边，如上图中（c）所示。

所以含有平行边或自环的图称为多重图

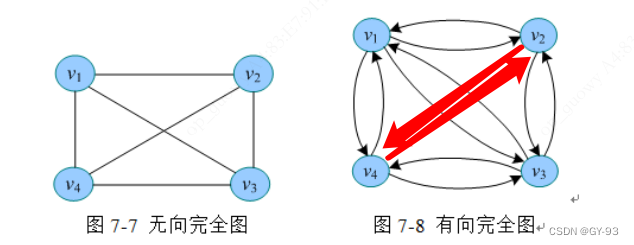
无向图中，任意两个点都有一个边，则该图称为无向完全图，如上图中7-7所示。含有n个顶点的无向图，每个点点到其它的n-1个顶点都有边，一共有(n*(n-1))/2条边

有向图中，任意两个带你都有两条方向相反的两条弧，则称该图为有向完全图，如上图中7-8所示。含有n个顶点的无向图，每个顶点发出n-1条边，一共有n * （n-1）条边。

稀疏图和稠密图：有很少或弧的图称为稀疏图，反之，称为稠密图。这是一个非常模糊的概念，很难讲多少洗漱，多少算稠密，一般来说，若图G满足|E|<|V|*log|V|,则称G为稀疏图。

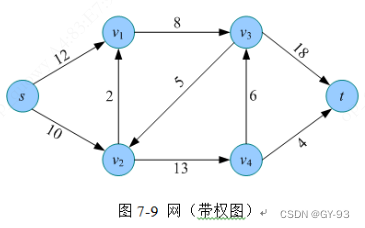
网：在实际应用中，经常在边上标注如距离、时间、耗费等数值，该数值称为边的权值。带权的图称为网。如上图所示

5.7 图的性质介绍

• 邻接和关联：
  • 邻接是指顶点和顶点之间的关系，关联是指边和顶点之间的关系。有边/弧相连的两个顶点之间的关系，如无向边（Vi,Vj）,则称Vi和Vj互为邻接点；有向边<Vi,Vj>,则称Vi邻接到Vj ,Vj邻接与Vi.若存在（Vi,Vj）或<Vi,Vj>，则称该边或弧关联与Vi和Vj,如下图所示：
  • **顶点的度：**顶点的度是指该顶点相关联的边的数目，记为TD(v).
  • **握手定理：**度数之和等于边数的两倍，即
• 路径、路径长度和距离
  • 路劲：接续的边的顶点构成的序列
  • 路径程度：路径上边或弧的数目
  • 距离：从顶点到另一顶点的最短路径长度
  • 子图：
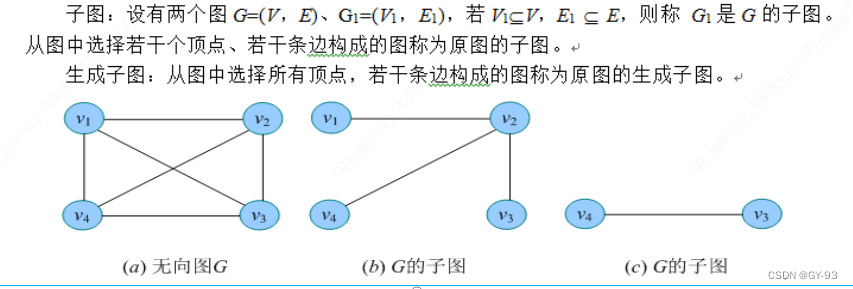
• 连通图和连通分量：
  
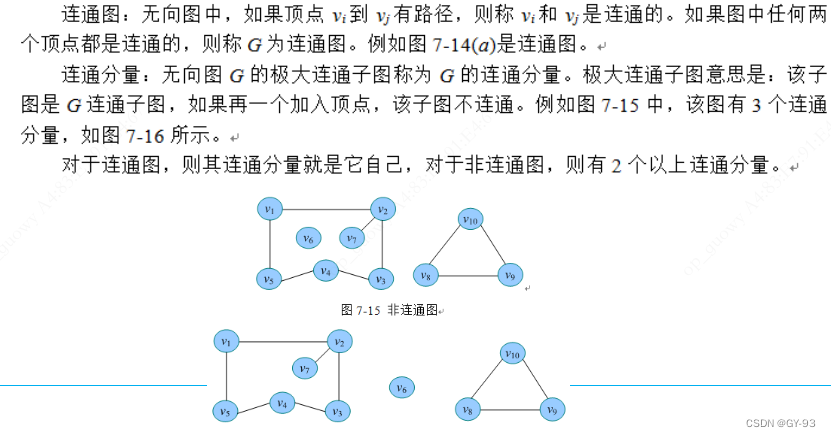
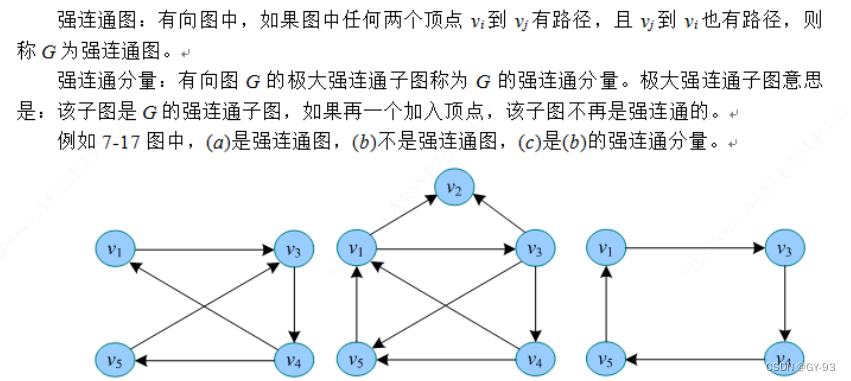
• 强连通图和强连通分量：