【中等】力扣算法题解析LeetCode223：矩形面积

关注文末的名片达文汐，回复关键词“力扣源码”，即可获取完整源码！！详见：源码和核心代码的区别

题目详情

给你二维平面上两个由直线构成且边与坐标轴平行/垂直的矩形，请你计算并返回两个矩形覆盖的总面积。

每个矩形由其左下顶点和右上顶点坐标表示：

• 第一个矩形由其左下顶点 (ax1, ay1) 和右上顶点 (ax2, ay2) 定义。
• 第二个矩形由其左下顶点 (bx1, by1) 和右上顶点 (bx2, by2) 定义。

示例 1：

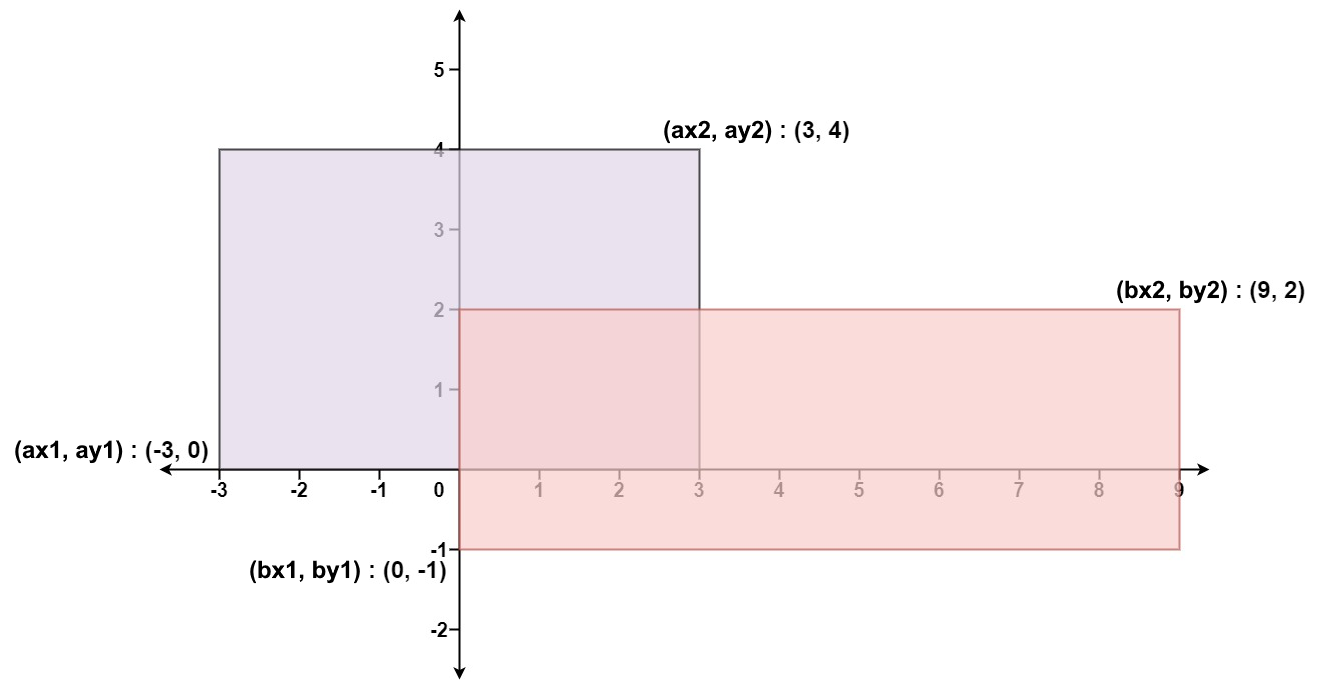
输入：ax1 = -3, ay1 = 0, ax2 = 3, ay2 = 4, bx1 = 0, by1 = -1, bx2 = 9, by2 = 2
输出：45

示例 2：
输入：ax1 = -2, ay1 = -2, ax2 = 2, ay2 = 2, bx1 = -2, by1 = -2, bx2 = 2, by2 = 2
输出：16

提示：

• -10^4 <= ax1, ay1, ax2, ay2, bx1, by1, bx2, by2 <= 10^4

---

解题思路

要计算两个矩形覆盖的总面积，需解决三个关键问题：

1. 计算两个矩形的面积：

   • 矩形1面积：width1×height1=(ax2−ax1)×(ay2−ay1)
   • 矩形2面积：width2×height2=(bx2−bx1)×(by2−by1)

2. 计算重叠区域面积：

   • 重叠宽度：取两矩形右边界的最小值减去左边界最大值（若结果为负说明无重叠，取0）：
     overlapWidth=max(0,min(ax2,bx2)−max(ax1,bx1))
   • 重叠高度：取两矩形上边界的最小值减去下边界最大值（若结果为负说明无重叠，取0）：
     overlapHeight=max(0,min(ay2,by2)−max(ay1,by1))
   • 重叠面积：overlapArea=overlapWidth×overlapHeight

3. 覆盖总面积：
   totalArea=area1+area2−overlapArea

---

代码实现（Java版）

class Solution {
    public int computeArea(int ax1, int ay1, int ax2, int ay2, int bx1, int by1, int bx2, int by2) {
        // 计算两个矩形的面积
        int area1 = (ax2 - ax1) * (ay2 - ay1);
        int area2 = (bx2 - bx1) * (by2 - by1);
        
        // 计算重叠部分的宽度和高度（若为负则取0）
        int overlapWidth = Math.max(0, Math.min(ax2, bx2) - Math.max(ax1, bx1));
        int overlapHeight = Math.max(0, Math.min(ay2, by2) - Math.max(ay1, by1));
        int overlapArea = overlapWidth * overlapHeight;
        
        // 覆盖总面积 = 两矩形面积之和 - 重叠区域面积
        return area1 + area2 - overlapArea;
    }
}

---

代码说明

1. 计算矩形面积：
   • 通过坐标差值直接求出两个矩形的面积 area1 和 area2。
2. 计算重叠区域：
   • 宽度：取两矩形右边界的最小值（min(ax2, bx2)）减去左边界最大值（max(ax1, bx1)），若结果为负说明无重叠，通过 max(0, ...) 归零。
   • 高度：同理取上边界最小值（min(ay2, by2)）减去下边界最大值（max(ay1, by1)），处理逻辑同宽度。
   • 重叠面积为宽度与高度的乘积。
3. 覆盖总面积：
   • 总面积 = 矩形1面积 + 矩形2面积 - 重叠区域面积，避免重复计算重叠部分。

---

提交详情（执行用时、内存消耗）

我的名片👇👇👇👇👇👇👇👇👇👇👇