Jensen不等式/琴生不等式的证明 数学归纳法

Table of Contents

凸函数

​​​​​​​琴生不等式/Jensen不等式

用数学归纳法来证明琴生不等式/Jensen不等式

---

​​​​​​​

​​​​​​​凸函数

​​​​​​​

一个函数如果满足

，

那么这个函数就是凸函数。

严格凸函数：≤改为<

​​​​​​​琴生不等式/Jensen不等式

如果是凸函数，那么对于任意的，以及正的权重系数，且，则如下不等式成立

用数学归纳法来证明琴生不等式/Jensen不等式

已知当n = 2时，此结论成立，如下：

对于一般的n用数学归纳法来证明。

假设n = N时此结论成立，需要证明n = N + 1时此结论成立

此时我们有N + 1 个点，以及权重，

令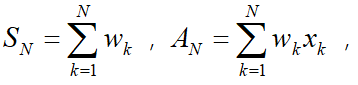

假设n = N时此结论成立，根据公式(1)即得出

 

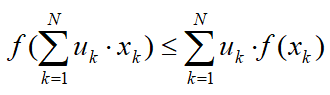
不等式左边：

 

不等式右边：

 

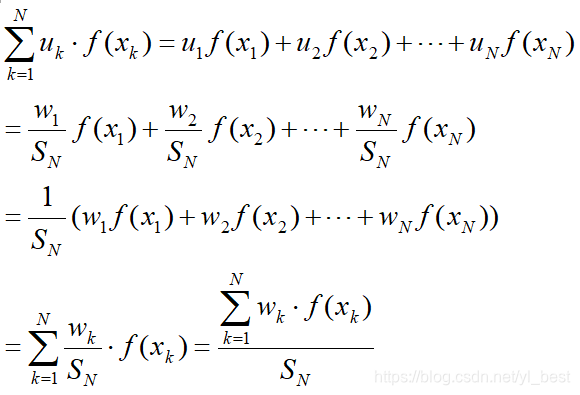
所以

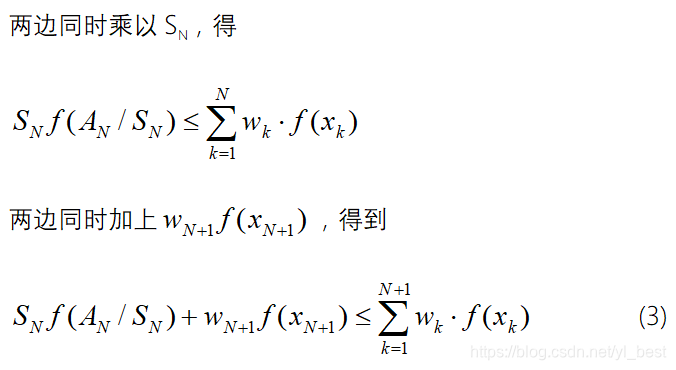
根据凸函数的定义

因为，所以公式(4)可以根据公式(2)（n=2的情况）类比得出(5)

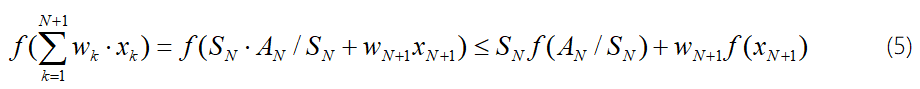
其中

结合不等式(3)(5)得出N+1的公式

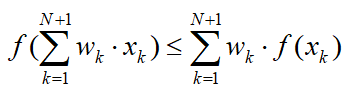
n = 2的情形已知成立，从n= N的情形出发，证明了n = N + 1的情形。

至此，公式证明完毕。