素数的快速判定

最新推荐文章于 2021-07-22 13:56:29 发布

原创最新推荐文章于 2021-07-22 13:56:29 发布 · 2.7k 阅读

1 ·

CC 4.0 BY-SA版权

算法篇专栏收录该内容

13 篇文章

订阅专栏

本文介绍了判断素数的三种方法，包括直观判断法及其改进，以及埃氏筛法和欧拉筛法。通过优化，避免了遍历到n-1的低效问题，提出只需遍历到sqrt(n)即可。同时，讨论了埃氏筛法可能存在的合数被多次筛选的问题，并介绍了欧拉筛法以确保每个合数只被筛选一次。

判断素数的方法

定义：“1不是质数。质数又称素数。一个大于1的自然数，除了1和它自身外，不能被其他自然数整除的数叫做质数；否则称为合数。所以1不是质数。质数的个数是无穷的。欧几里得的《几何原本》中有一个经典的证明。它使用了证明常用的方法：反证法。”约数只有1和本身的整数称为质数，或称素数。

Level 1:我们最先学的简单粗暴的质数函数判定

就像是这样：

bool is_prime(int x)
{
    if(x==0 || x==1) return false;//0和1不是素数
    if(x==2) return true;//2是素数
    for(int i=2;i*i<=x;i++)枚举2~sqrt(i)中的因数
    {
        if(x%i==0) return false;//如果这个数不包括自己和1之外有因数，说明这个数不是素数
    }
    return true;//如果除了1和自己外没有因数，说明是素数
}

这种方法的时间复杂度很大，一般在OI中不建议使用

1.直观判断法：

最直观的方法，根据定义，因为质数除了1和本身之外没有其他约数，所以判断n是否为质数，根据定义直接判断从2到n-1是否存在n的约数即可。java代码如下：

import java.util.*;

public class Main5 {
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		int n = sc.nextInt();
		int ok = 0;
		for (int i = 2; i < n; i++) {
			if (n % i == 0) {
				ok = 1;
				break;
			}
		}
		if (ok == 0) {
			System.out.println("素数");
		} else {
			System.out.println("不是素数");
		}
	}
}

2.直观判断法改进
上述判断方法，明显存在效率极低的问题。对于每个数n，其实并不需要从2判断到n-1，我们知道，一个数若可以进行因数分解，那么分解时得到的两个数一定是一个小于等于sqrt(n)，一个大于等于sqrt(n)，据此，上述代码中并不需要遍历到n-1，遍历到sqrt(n)即可，因为若sqrt(n)左侧找不到约数，那么右侧也一定找不到约数。java代码如下：

import java.math.BigDecimal;
import java.math.BigInteger;
import java.util.*;

public class Main3{
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		int n = sc.nextInt();
		int ok=0;
		for (int i = 2; i <=Math.sqrt(n) ; i++) {
			if(n%i==0) {
				ok=1;
				break;
			}
		}	
		if(ok==0) {
			System.out.println("素数");
		}else {
			System.out.println("不是素数");
		}			
				
	}
}

例题：

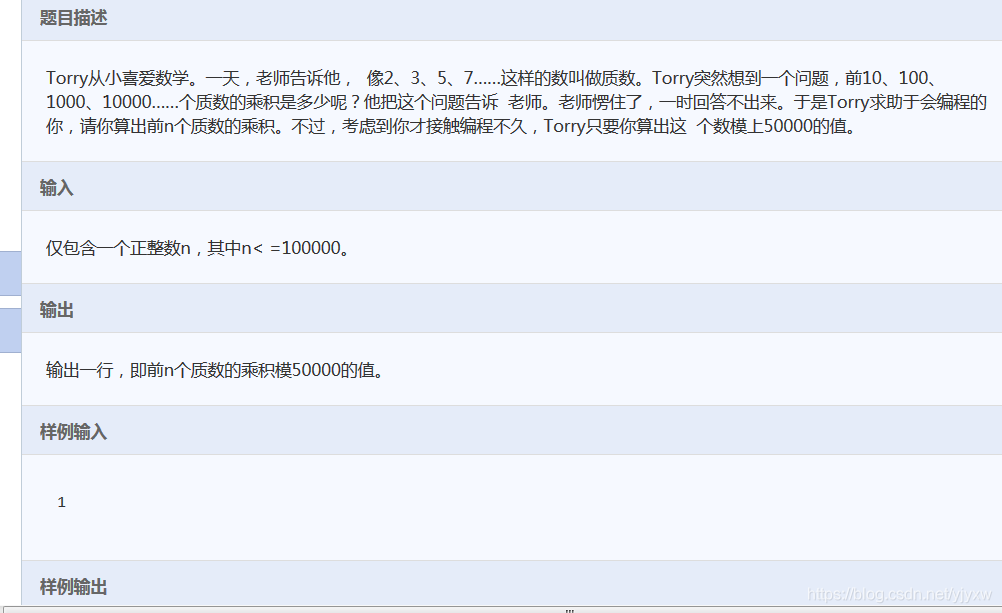
代码：

import java.math.BigInteger;
import java.util.*;

public class Main {
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		while (sc.hasNext()) {
		    long n  = sc.nextLong();
			int jj = 0;
			long sum = 1l;
				ff:for (int i = 2;; i++) {
					for (int j = 2; j <=Math.sqrt(i); j++) {
						if (i % j == 0) {
							jj++;
						}
					}
					if (jj == 0) {
						sum = (sum*i)%50000;
						n--;
						if(n==0) {
							break ff;
						}
					}
					jj = 0;
				}
           System.out.println(sum);
		}
	}
}

测评结果：

分析：判断有一个数被除开之后应该立即跳出循环！！break！！

代码改进：

import java.math.BigInteger;
import java.util.*;

public class Main {
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		while (sc.hasNext()) {
		    long n  = sc.nextLong();
			int jj = 0;
			long sum = 1l;
				ff:for (int i = 2;; i++) {
					for (int j = 2; j <=Math.sqrt(i); j++) {
						if (i % j == 0) {
							jj++;
							break;
						}
					}
					if (jj == 0) {
						sum = (sum*i)%50000;
						n--;
						if(n==0) {
							break ff;
						}
					}
					jj = 0;
				}
           System.out.println(sum);
		}
	}
}

测评结果：

例题（杭电oj1215）：

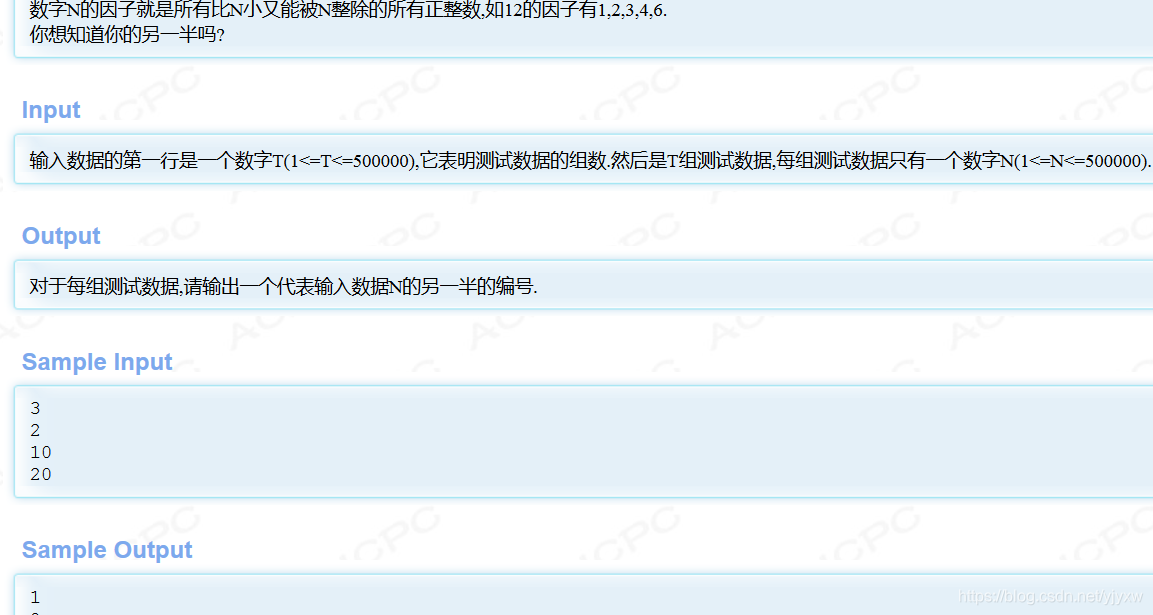
分析及题意：求出所有约数之和，一个数若可以进行因数分解，那么分解时得到的两个数一定是一个小于等于sqrt(n)，一个大于等于sqrt(n)，据此，上述代码中并不需要遍历到n-1，遍历到sqrt(n)即可，因为若sqrt(n)左侧找不到约数，那么右侧也一定找不到约数。所以只要找出左面的约数，右面的也就知道了。注意9=3*3

例如20的约数是：

1 2 4 $\sqrt{20}$ $根号20$ 5 10；遍历到2 ，右面的等于20/2=10 ，遍历到4，右面的等于20/4=5。

代码实现：

import java.util.Scanner;

public class Main2 {
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		while (sc.hasNext()) {
			int n = sc.nextInt();
			while (n-- > 0) {
				int a = sc.nextInt();
				long sum = 0l;
				for (int j = 1; j <= Math.sqrt(a); j++) {
					if (a % j == 0) {
						sum += j;
						if (j * j != a) {
							if (j != 1) {
								sum += a / j;
							}
						}
					}
				}
				System.out.println(sum);
			}

		}
	}
}

总结：

一个数若可以进行因数分解，那么分解时得到的两个数一定是一个小于等于sqrt(n)，一个大于等于sqrt(n)，据此，上述代码中并不需要遍历到n-1，遍历到sqrt(n)即可，因为若sqrt(n)左侧找不到约数，那么右侧也一定找不到约数。

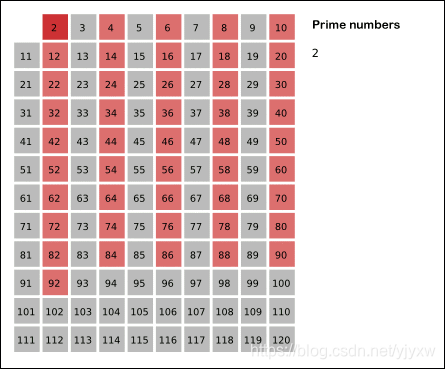
判断前2到n个数的所有素数，其中最小的数字2是素数。将表中所有2的倍数都划去。表中剩余的最小数字是3，它不能被更小的数整除，所以是素数。再将表中所有3的倍数全都划去。依次类推，如果表中剩余的最小数字是m时，m就是素数。然后将表中所有m的倍数全部划去。像这样反复操作，就能依次枚举n以内的素数

Level 2:埃氏筛法

基本思想：从2开始，将每个质数的倍数都标记成合数，以达到筛选素数的目的。

代码：

int visit[maxn];  
void Prime(int n)
{
memset(visit,0,sizeof(visit));//初始化都是素数
visit[0]=visit[1]=1;//0和1不是素数
for(int i=2;i<=n;i++) {
    if(!visit[i])//如果i是素数，让i的所有倍数都不是素数
    {        
        for (int j=i;j<=n;j+=i)
        { 
            visit[j] = 1;
        }
    }
}

但是埃氏筛法有缺陷：对于一个合数，有可能被筛多次。例如30=2×15=3×10= 5×6……那么如何确保每个合数只被筛选一次呢？我们只要用它的最小质因子来筛选即可，这便是欧拉筛法。

Level 3:欧拉筛法

基本思想：在埃氏筛法的基础上，让每个合数只被它的最小质因子筛选一次，以达到不重复的目的。
代码：

int prime[maxn];
int visit[maxn];
void Prime(int n){
    memset(visit,0,sizeof(visit));
    memset(prime,0,sizeof(prime));
    for(int i=2;i<=n;i++) {
        if(!visit[i]) {
            prime[++prime[0]]=i;//记录素数，这个prime[0]相当于cnt，用来计数
        }
        for(int j=1;j<=prime[0] && i*prime[j]<=maxn;j++) {
            visit[i*prime[j]] = 1;
            if (i%prime[j] == 0) {
                break;
            }
        }
    }
}