jzoj2019.03.09【NOIP提高组】模拟 B组 快速幂+状压搜索+辗转相除

T1单峰

可以发现，峰顶一定是n，因此考虑1~n-1 分别放在n 的左边还是右边，一一得出相应的唯一方案。所以答案就是2^(n-1)
再由数据范围可知用快速幂即可
快速幂就是求x^n时，每逢n的二进制位为1时才操作答案。在快速幂中可以随时%

#include <cstdio>

using namespace std;

const long long mo=1e9+7;
long long n,ans;

void ksm(long long x,long long y){
	ans=1;
	while (x){
		if (x&1==1) {					
			ans=(ans*y)%mo;							
		}
		y=(y*y)%mo;
		x>>=1;
	}
}

int main(){
	scanf("%lld",&n);
	ksm(n-1,2);
	printf("%lld",ans);
}

T2积木

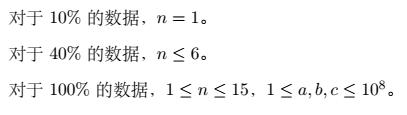
那么，由n的数量之少以及状态之多可知用状态压缩

对于状态压缩有

取出第i位	第i位赋为1
x&(1<<i)	x or (1<<i)

显然是状态压缩DP。设计状态f[S][i][0/1/2] 表示已经⽤了集合S 内的积⽊，最顶上是编
号为i 的积⽊，它的哪个⾯朝上。转移时枚举不在S 内的积⽊，以及朝上的⾯判断即可。时间
复杂度O(2n*(3n)^2)。
然后利用状态压缩进行记忆化搜索也行
剪枝方式有
1.用状态压缩表示第i块积木是否已用；
2.将a,b,c简单排序，可以规定长是较小的而宽则为较大的，如此则枚举每一块积木时只需找a,b,c分别做为高度的情况，因为长宽的顺序是 已固定的，且这种固定对答案不会有影响；

#include <cstdio>
#include <algorithm>

using namespace std;

int n,ans;
int a[20],b[20],c[20];

void dfs(int dep,int h,int ch,int k,long long x){
	if (dep>n) return;
	for (int i=1;i<=n;i++)
	if ((x&(1<<i))==0){
		if (a[i]<=ch){
			if (b[i]<=k){
				dfs(dep+1,h+c[i],a[i],b[i],x|1<<i);
			}
			if (c[i]<=k){
				dfs(dep+1,h+b[i],a[i],c[i],x|1<<i);
			}
		}
		if ((b[i]<=ch)&&(c[i]<=k)){
			dfs(dep+1,h+a[i],b[i],c[i],x|1<<i);
		}
	}
	if (h>ans) ans=h;
}

int main(){
	scanf("%d",&n);
	for (int i=1;i<=n;i++){
		scanf("%d%d%d",&a[i],&b[i],&c[i]);
		if (a[i]>b[i]) swap(a[i],b[i]);
		if (a[i]>c[i]) swap(a[i],c[i]);
		if (b[i]>c[i]) swap(b[i],c[i]);
	}
	dfs(0,0,1e8,1e8,0);
	printf("%d",ans);
}

T3看电影

听说NOIP2016大家都考得不错，于是CCF奖励省常中了 K 张变形金刚5的电影票奖励OI队的同学去看电影。可是省常中OI队的同学们共有 N（N >= K）人。于是机智的你想到了一个公平公正的方法决定哪K人去看电影。
N个人排成一圈，按顺时针顺序标号为1 - N，每次随机一个还存活的人的编号，将这个人踢出。继续上述操作，直到剩下K个人。
但这样显然太无聊了，于是小S又想出一个牛逼的方法。
N个人排成一圈，按顺时针顺序标号为1 - N，每次随机一个1 - N的编号，假设随机到的编号是X，如果编号为X人还未踢出，则将这个人踢出，否则看编号为X % N + 1（即顺时针顺序下一个编号）的人是否存活，如果还未踢出则将他踢出，否则继续看编号（X + 1）% N +1的人，如果已被踢出看顺时针的下一个…………，以此类推，直到踢出一个人为止。重复上述操作，直到剩下K个人。
已知小S的编号是Id，问按照小S的方法来他有多少的概率可以不被踢出，成功得到看电影的机会。

由于每次随机到每个人的几率是固定的，所以每次每个人被踢出的概率都相等
可得无论Id值几何，概率都是k/n，结果是k/n化为最简分数
这时可以用辗转相除求出k,n的最大公因数

#include <cstdio>
#include <iostream>

using namespace std;

int n,k,id,c;

int gcd(int a,int b){
	if (b==0) return a;
		else return gcd(b,a%b);
}

int main(){
	scanf("%d%d%d",&n,&k,&id);
	if (k==n) printf("1/1"); else
	if (k==0) printf("0/1"); else
	if (k==1) printf("1/%d",n); else{
		c=gcd(n,k);
		printf("%d/%d",k/c,n/c);
	}
	cout<<(4&2);
}

冠盖满京华，斯人独憔悴