Buck电路小信号建模仿真及控制器设计

图1.Buck电路拓扑

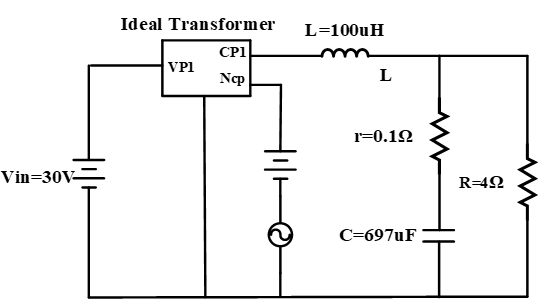
1.状态空间表达式

                                                                                  

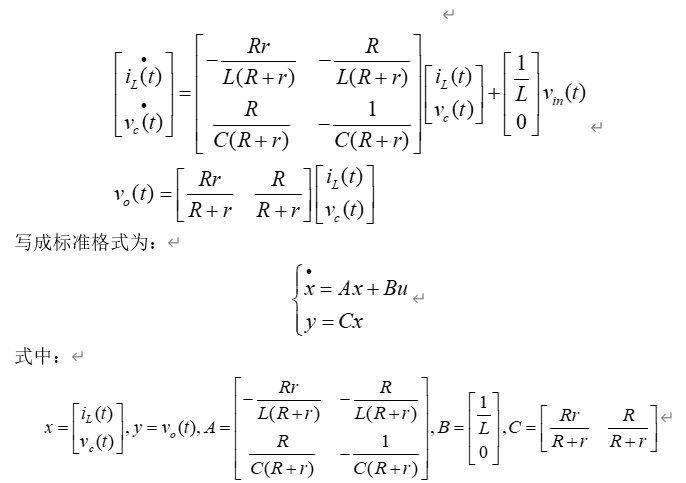
2.状态平均表达式

3.小信号动态模型

4.Gps(s)求解

5.Bode图绘制

        由Gps传递函数编写M语言如下：

n = [3e4,4.3042e8];

d= [1,1358.6801,1.4372e7];

margin(n,d);grid on

        用MATLAB画出其幅频与相频特性曲线如下图所示：

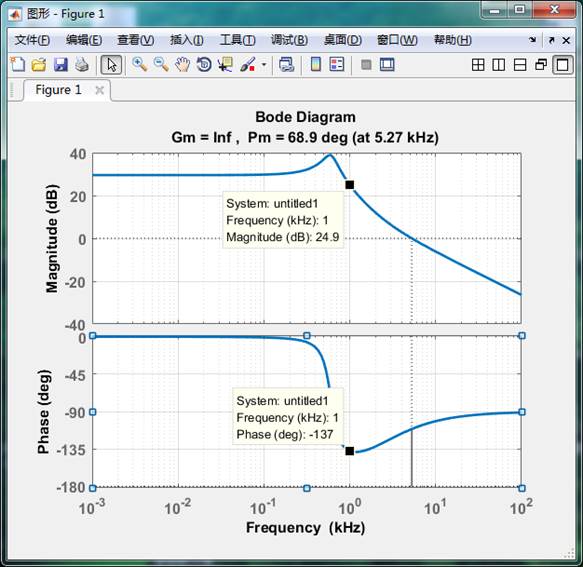
图2.小信号模型Gps幅频特性

6.反馈控制器设计

（a）控制器传递函数求解：

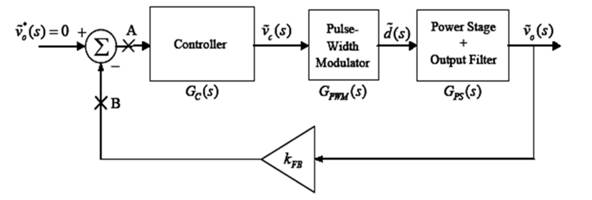
图3.小信号模型控制框图

（b）用运算放大器搭建控制器：

        控制器电路如下，可在Psim中进行搭建仿真

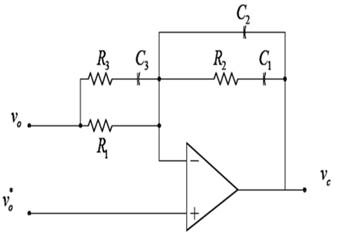
图4.控制器电路模块

7.建模仿真

        分别在simulink和Psim中建立仿真模型，进行仿真分析对比，其中simulink中的控制器以传递函数进行表示，而Psim中则用运算放大器和电阻电容元件搭建传递函数，从而实现矫正功能。

（a）matlab建模仿真

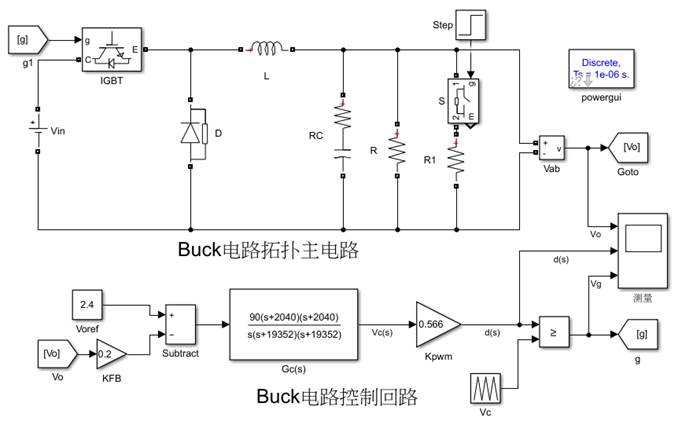
图5. Simulink仿真模型

        仿真模型包括主电路和控制回路，其中主电路为Buck电路各参数如前所述，仿真总时长为3s，在2s时刻，突加负载，即输出电阻R两端并联一个10Ω的电阻R1。输出电压稳压在12V，经反馈系数与参考电压比较，通过反馈控制器矫正后与三角波比较得到占空比，从而调节开关管开通关断实现稳压。

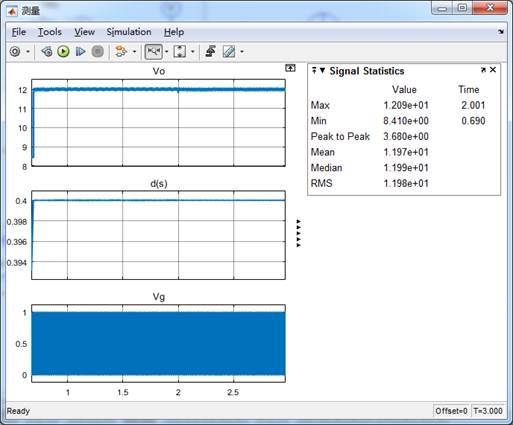
图6.Simulink仿真整体图

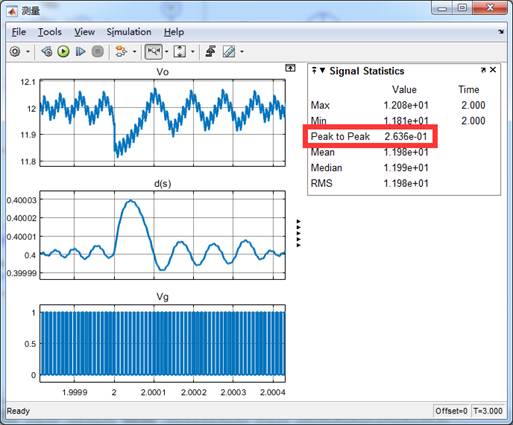
图7. Simulink仿真局部图

        图中波形由上至下分别是输出电压，占空比和开关管驱动信号，由仿真结果可知，系统能较好的稳定在12V输出，开关管占空比稳定在0.4，当2s时，突加负载瞬间，误差低于0.26V，且在0.4ms内基本恢复稳定，说明系统动态及稳态性能均较好。

（b）Psim建模仿真

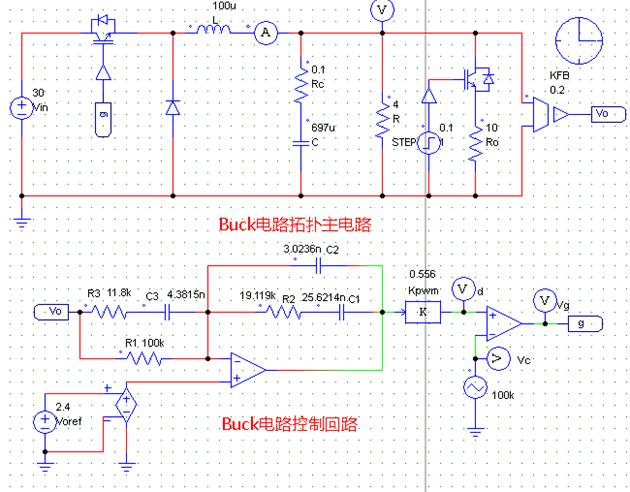
图8. Psim仿真模型

        按前述计算结果搭建控制器如上图所示，仿真总时长0.2s，在0.1s处突加负载，输出并联一个10Ω电阻，仿真结果如下。此处仅用于理论仿真，对实际电路元器件参数选型具有一定指导意义。

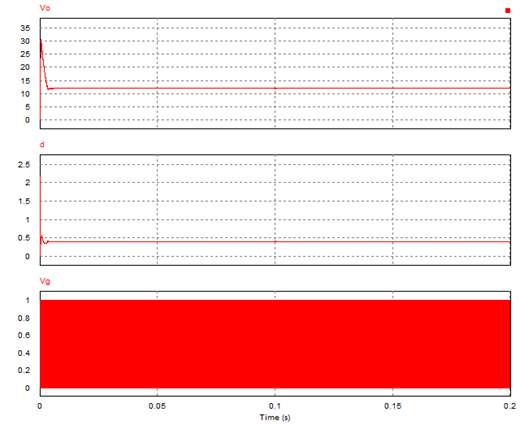
图9.Psim仿真整体图

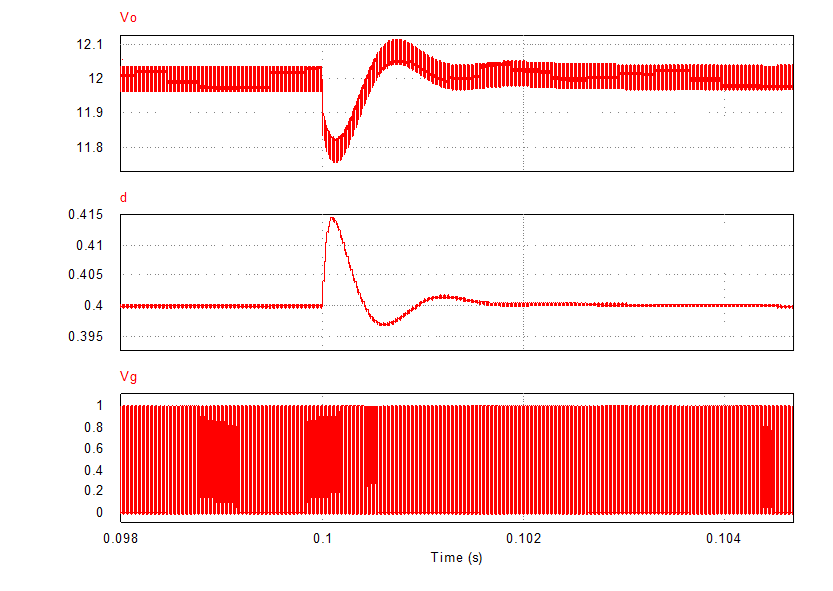
图10.Psim仿真局部图一

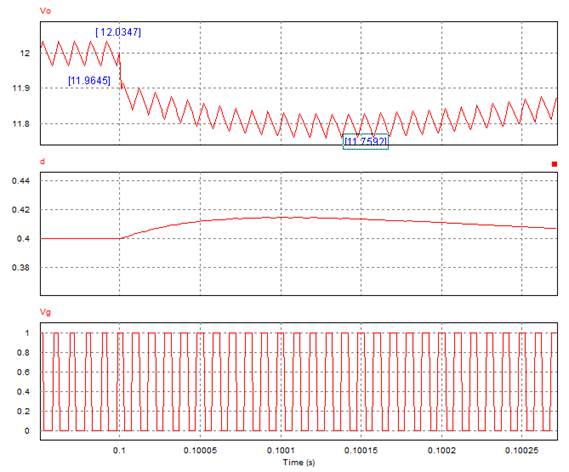
图11. Psim仿真局部图二

        图中波形由上至下分别是输出电压，占空比和开关管驱动信号，由仿真结果可知，系统能较好的稳定在12V输出，开关管占空比稳定在0.4，当0.1s时，突加负载瞬间，误差低于0.276V，且在0.4ms内基本恢复稳定，（与Simulink仿真结果一致）说明系统动态及稳态性能均较好。

负载突变瞬间电压略微跌落

现象：对比分析simulink和psim模型发现，无论是用传递函数作为控制器还是用运放搭建控制器，在负载突增时，均会发现电压有一个微小的跌落，由图11Vo波形数据可知电压跌落约为11.759V。

分析：因为负载突增前，负载电阻为4Ω，输出电压稳态为12V，稳态电容电压计算得，当负载突增瞬间，电容电压保持不变，外电阻并联一个10Ω电阻后减小为，分压减小，所以负载突变瞬间，外电阻端电压即输出电压，与仿真测量结果11.759V近似相等。

8.总结

        首先根据开关管不同导通状态，分析电路导通情况，根据KVL，KCL列写各状态下的电路微分方程，整理成标准形式，并求出平均状态模型，在此基础上推导出小信号动态模型，求解对应传递函数及其幅频特性，根据系统设计要求，选定控制器形式及反馈系数等，并计算控制器传递函数（可根据传递函数用电路搭建控制器），之后搭建仿真模型进行验证，通过加入扰动，分析验证设计的控制系统的动态特性及稳态特性。