leetcode50.Pow(x,n)(java)：快速幂

最新推荐文章于 2025-03-18 10:19:22 发布

原创最新推荐文章于 2025-03-18 10:19:22 发布 · 181 阅读

0 ·

CC 4.0 BY-SA版权

leetcode 专栏收录该内容

87 篇文章

订阅专栏

本文深入探讨了快速幂运算的两种高效实现方法：递归与迭代。递归方法利用分治策略，将大问题分解为小问题，显著降低计算复杂度至O(logn)。迭代方法则通过循环操作，避免了递归带来的额外空间开销，实现了O(1)的空间复杂度。文章详细介绍了每种方法的具体步骤与代码实现，适用于处理大规模幂运算场景。

题目
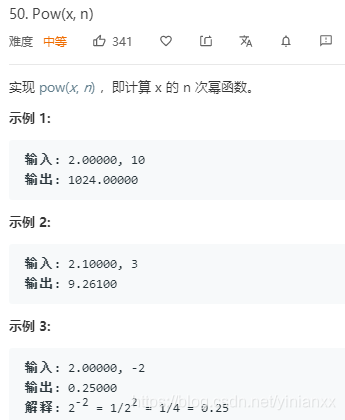
在这里插入图片描述
n为负数，可以转换为1.0/x^-n，所以把n看成自然数来处理即可。
方法一：递归
两种情况

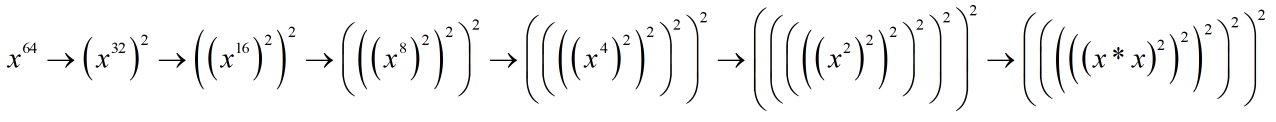
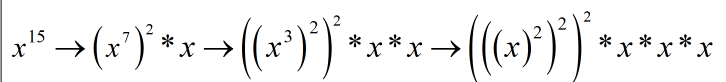
递归结束条件：
如果n==0，return1.0；

递归过程：
y = f(x,n/2)
如果n为奇数，返回值为yy
否则，返回值为yy*x。

具体代码

class Solution {
    public double quickMul(double x, long N){
        if(N == 0){
            return 1.0;
        }
        double y = quickMul(x,N/2);
        return N % 2 == 0?y*y:y*y*x;
    }
    public double myPow(double x, int n) {
        long N = Math.abs(n);
        return n >= 0? quickMul(x,N):1.0/quickMul(x,N);
    }
}

时间复杂度：O(logn)
空间复杂度：O(logn)

方法二：迭代
比如计算2^13
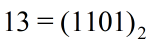
15 = (1101)
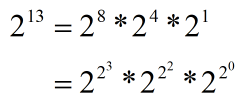
在这里插入图片描述
判断n的第i位是否为1，为1则

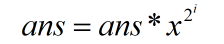
每次循环n = n/2，x=x*x

具体代码

class Solution {
    public double quickMul(double x, long N){
        double ans = 1.0;
        double x_temp = x;
        while(N > 0){
            if(N % 2 == 1){
                ans *= x_temp;
            }
            x_temp *= x_temp;
            N /=2;
        }
        return ans;
    }
    public double myPow(double x, int n) {
        long N = n;
        return n >= 0? quickMul(x,N):1.0/quickMul(x,-N);
    }
}