栈及波兰表达式

栈的特点：

先进后出

栈的方法：

stack.pop():弹出最上层的数据，并弹出数据
stack.push():在栈的最上层压入数据
stack.peek():查看栈的最上层数据，但是不弹出数据

表达式：

表达式分前缀表达式、中缀表达式和后缀表达式。
中缀表达式：人类最熟悉的一种表达式1+2，(1+2)3，3+42+4等等都是中缀表示法。
前缀表达式又叫做波兰式，前缀表达式为- + A * B - C D * E F
后缀表达式又叫做逆波兰式。形如：A B C D - * + E F * -

中缀表达式对于计算机的运算并不便利，而前缀后缀表达式的计算相对简单方便。因此，需要将中缀表达式转换成前缀后缀表达式，然后利用栈结构计算前后缀表达式。

栈结构计算后缀表达式：

    public static void main(String[] args) {
        ReversePolandNotation poland = new ReversePolandNotation();
        String suffixExpression = "30 4 + 5 * 6 -";
        String result =  poland.caculate(poland.getArray(suffixExpression));
        System.out.println(result);
    }

    //计算得到表达式结果
    public String caculate(String[] arrays){
        Stack<String> stack = new Stack<>();
        for(String str : arrays){
            if(str.matches("\\d+")){
                stack.push(str);
            }else{
                int num2 = Integer.parseInt(stack.pop());
                int num1 = Integer.parseInt(stack.pop());
                if("+".equals(str)){
                    stack.push(String.valueOf(num1 + num2));
                }else if("-".equals(str)){
                    stack.push(String.valueOf(num1 - num2));
                }else if("*".equals(str)){
                    stack.push(String.valueOf(num1 * num2));
                }else if("/".equals(str)){
                    stack.push(String.valueOf(num1 / num2));
                }else{
                    throw new RuntimeException("操作符不对");
                }
            }
        }
        return stack.pop();
    }

    //表达式根据空格分隔得到数组和操作符的数组
    public String[] getArray(String expression){
        if(expression != null){
            String[] arrays = expression.split(" ");
            return arrays;
        }
        return null;
    }

中缀表达式转后缀表达式

1、转化原理：

2、转化示例：

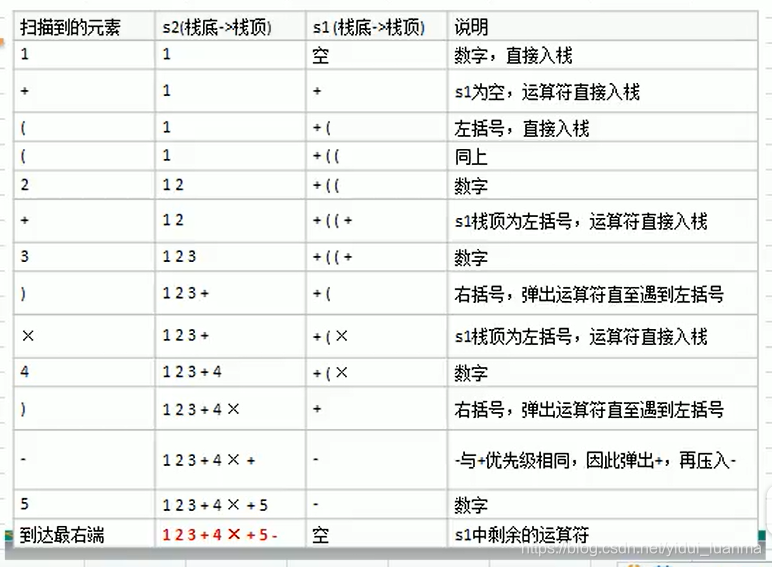
3、转化代码：

   public class PolandNotationChange {
public static void main(String[] args) {
    PolandNotationChange poland = new PolandNotationChange();
    String middleExpression = "1 + ( ( 2 + 3 ) * 4 ) - 5";
    //1、表达式转为数组
    String[] middleArray = poland.getArray(middleExpression);
    //2、中缀转后缀
    String suffixExpression = poland.changeExpression(middleArray);
    //3、后缀倒叙输出
    String reverseExpression = new StringBuilder(suffixExpression).reverse().toString();
    System.out.println("中缀表达式“"+middleExpression + "”转化为后缀表达式：“"+reverseExpression + "”");
    String result = new ReversePolandNotation().caculate(poland.getArray(reverseExpression));
    System.out.println("最终计算结果："+result);
}
//2、中缀转后缀
private String changeExpression(String[] middleArray) {
    Stack<String> resultStack = new Stack<>();
    Stack<String> operStack = new Stack<>();

    for(String str : middleArray){
        if(str.matches("\\d+")){
            resultStack.push(str);
        }else if("+".equals(str) || "-".equals(str) || "*".equals(str) || "/".equals(str)){
            pushOperStack(resultStack,operStack,str);
        }else if("(".equals(str)){
            operStack.push(str);
        }else if(")".equals(str)){
            pushRightStack(resultStack,operStack);
        }

    }

    while(true){
        if(operStack.isEmpty()){
            break;
        }
        resultStack.push(operStack.pop());
    }

    StringBuilder sb = new StringBuilder();
    while(true){
        if(resultStack.isEmpty()){
            sb.replace(sb.length()-1,sb.length(),"");
            break;
        }
        sb.append(resultStack.pop()).append(" ");
    }
    return sb.toString();
}

//5、压栈时右括号处理
public void pushRightStack(Stack<String> resultStack,Stack<String> operStack){
    String topOper = operStack.pop();
    if("(".equals(topOper)){
        return;
    }else{
        resultStack.push(topOper);
        pushRightStack(resultStack,operStack);
    }
}

//4、压栈时运算符处理
public void pushOperStack(Stack<String> resultStack,Stack<String> operStack,String oper){
    if(operStack.isEmpty()){
        operStack.push(oper);
    }else{
        String topOper = operStack.pop();
        if( "(".equals(topOper) ){
            operStack.push(topOper);
            operStack.push(oper);
        }else if(priority(oper) > priority(topOper)){
            operStack.push(topOper);
            operStack.push(oper);
        }else{
            resultStack.push(topOper);
            pushOperStack(resultStack,operStack,oper);
        }
    }
}

//3、获取运算符优先级
public int priority(String oper){
    if("+".equals(oper)){
        return 1;
    }else if("-".equals(oper)){
        return 1;
    }else if("*".equals(oper)){
        return 2;
    }else if("/".equals(oper)){
        return 2;
    }
    throw new RuntimeException("运算符不正确");
}


//1、表达式根据空格分隔得到数组和操作符的数组
public String[] getArray(String expression){
    if(expression != null){
        String[] arrays = expression.split(" ");
        return arrays;
    }
    return null;
}