支持向量机SVM——自学第十篇

最新推荐文章于 2025-05-08 19:17:43 发布
原创 最新推荐文章于 2025-05-08 19:17:43 发布 · 530 阅读 · 3 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文深入探讨支持向量机(SVM)原理，涵盖线性与非线性分类，软边际与正则化概念，以及SVM在sklearn中的实现与应用，包括回归问题的解决。

1、支持向量机

可以解决分类问题，也可以解决回归问题
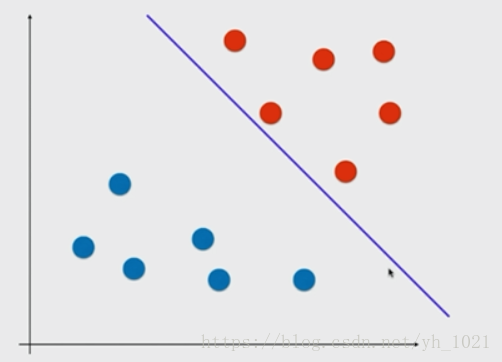
在这里插入图片描述
在上图所示中，有两类数据，如果使用逻辑回归，那在两组数据中找出一条分界线即可，当然这个分界线有很多种可能。如果有一个新的数据，是靠近红色点的那一边，但是没有过线而被分为了蓝色点，在这种情况下的模型的泛化能力是不高的。
我们选择另一条分割线，使得两组数据距离直线的最近距离相等，这样的模型泛化能力较高。
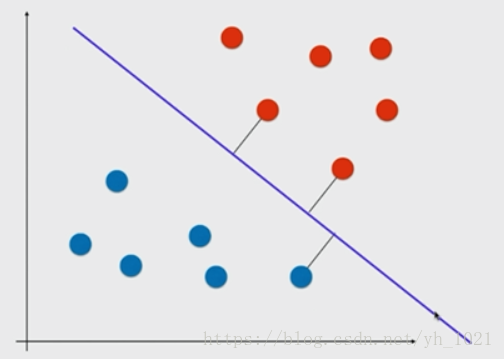
在这里插入图片描述
再画出两条与分割线相平行的直线，使得在这两条直线当中没有数据点。
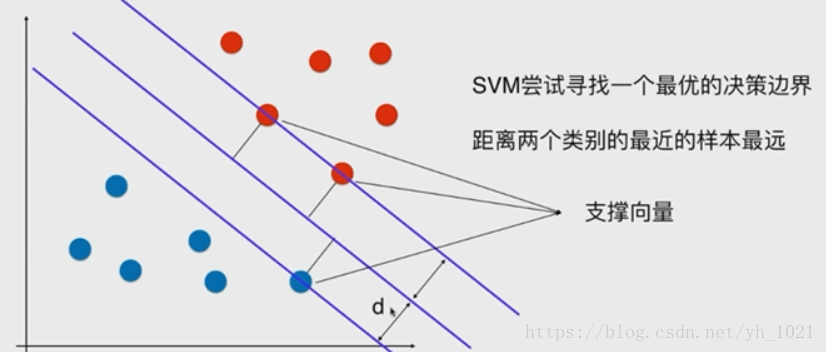
在这里插入图片描述
在边界线上的数据点叫做支撑向量，两条边界线之间的距离叫做margin（2*d），中间的线叫做最优决策边界，而svm分类器要做的，就是最大化这个margin。这种方法是解决线性可分问题，叫做Hard Margin SVM，解决线性不可分的问题需要用Soft Margin SVM。

2、数学推导（Hard Margin SVM）

（x,y）到直线Ax+By+C=0的距离为∣Ax+By+C∣A2+B2\frac{\left | Ax+By+C \right |}{\sqrt{A^{2}+B^{2}}}A2+B2​∣Ax+By+C∣​，拓展到n维空间，到中间直线wTx+b=0w^{T}x+b=0wTx+b=0的距离为∣wT+b∣∥w∥\frac{\left | w^{T}+b \right |}{\left \| w \right \|}∥w∥∣wT+b∣​，其中∥w∥=w12+w22+...+wn2\left \| w \right \|=\sqrt{w_{1}^{2}+w_{2}^{2}+...+w_{n}^{2}}∥w∥=w12​+w22​+...+wn2​​。
若点到直线的距离>d，则y取1；若将点带入距离公式并去掉绝对值<-d，则y取0>。将d除到左边后可以得到式子：
wTx(i)+b≥1w^{T}x^{\left ( i \right )}+b\geq 1wTx(i)+b≥1，则y取1；wTx(i)+b≤−1w^{T}x^{\left ( i \right )}+b\leq -1wTx(i)+b≤−1，则y取0。
还可以化简为：y(i)(wTx(i)+b)≥1y^{\left ( i \right )}\left ( w^{T}x^{\left ( i \right )}+b \right )\geq 1y(i)(wTx(i)+b)≥1
目标函数为：max∣wT+b∣∥w∥\frac{\left | w^{T}+b \right |}{\left \| w \right \|}∥w∥∣wT+b∣​，因为支持向量带入决策边界方程后分子均为1，所以
目标函数:在：y(i)(wTx(i)+b)≥1y^{\left ( i \right )}\left ( w^{T}x^{\left ( i \right )}+b \right )\geq 1y(i)(wTx(i)+b)≥1的条件下max1∥w∥\frac{1}{\left \| w \right \|}∥w∥1​，(最小化12∥w∥2\frac{1}{2}\left \|w \right \|^221​∥w∥2），这是有条件的最优化问题。

3、Soft Margin和SVM的正则化

为了提高泛化能力和容错能力，在分类时需要不考虑一些极度特殊的点和错误的点。所以就要用到soft margin svm。因为在hard margin svm中，给定的限定条件是必须在>1和<-1的两根直线之外，为了增加容错能力，将两根直线之间的距离稍微小一点（即允许两根线之间有一些点）。需满足：
y(i)(wTx(i)+b)≥1−ξiy^{\left ( i \right )}\left ( w^{T}x^{\left ( i \right )}+b \right )\geq 1-\xi_{i}y(i)(wTx(i)+b)≥1−ξi​，（ξi≥0\xi _{i}\geq 0ξi​≥0）
为了不使ξ\xiξ无穷大，在目标函数后面增加一项，变成：
min12∥w∥2+∑i=1mCξi\frac{1}{2}\left \| w \right \|^2+\sum_{i=1}^{m}C\xi _{i}21​∥w∥2+∑i=1m​Cξi​
这样使得最小化目标函数的同时能有效抑制ξ\xiξ，同时该项也起到了L1正则化的目的，当然L2正则化就是使用的ξ\xiξ的平方。
C的值越小，给予的容错空间越大，当C=0时，就为Hard Margin SVM。

4、sklearn中实现SVM（分类）

因为计算最大间隔涉及距离，所以如果在不同的维度上量纲不同的话，会使得量纲大的那个维度的数占主导地位。所以在进行svm之前也需要做数据的标准化处理。

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets

iris=datasets.load_iris()
x=iris.data
y=iris.target
#这里只做二分类问题
x=x[y<2,:2]
y=y[y<2]

plt.scatter(x[y==0,0],x[y==1,1],color='r')
plt.scatter(x[y==1,0],x[y==1,1],color='b')
plt.show()

#对数据进行标准化
from sklearn.preprocessing import StandardScaler
standardscaler=StandardScaler()
standardscaler.fit(x)
x_standard=standardscaler.transform(x)

#加载线性SVM，进行分类工作
##SVC默认采用ovr，多分类时可以改成ovo；默认使用L2方式，也可以使用L1正则化
from sklearn.svm import LinearSVC
svc=LinearSVC(C=1e11)  #C取值越小，容错空间越大
svc.fit(x_standard,y)

#画出决策边界以及两条边界线
def plot_svc(axis):
    w0=svc.coef_[0]
    b=svc.intercept_[0]
#w0*x0+w1*x1+b=0    x1=-w0/w1*x0-b/w1
    plot_x=np.linspace(axis[0],axis[1],200)
    plot_y=-w0[0]/w0[1]*plot_x-b/w0[1]
#画出svm的上下边界，w0*x0+w1*x1+b=1 ，x1=-w0/w1*x0-b/w1+1/w1
    up_y=-w0[0]/w0[1]*plot_x-b/w0[1]+1/w0[1]
    down_y=-w0[0]/w0[1]*plot_x-b/w0[1]-1/w0[1]
    plt.plot(plot_x,plot_y,color='black')
#将上下边界的y轴范围确定在图的范围之内
    up_index=(up_y>=axis[2])&(up_y<=axis[3])
    down_index=(down_y>=axis[2])&(down_y<=axis[3])
    plt.plot(plot_x[up_index],up_y[up_index],color="r")
    plt.plot(plot_x[down_index],down_y[down_index],color="r")
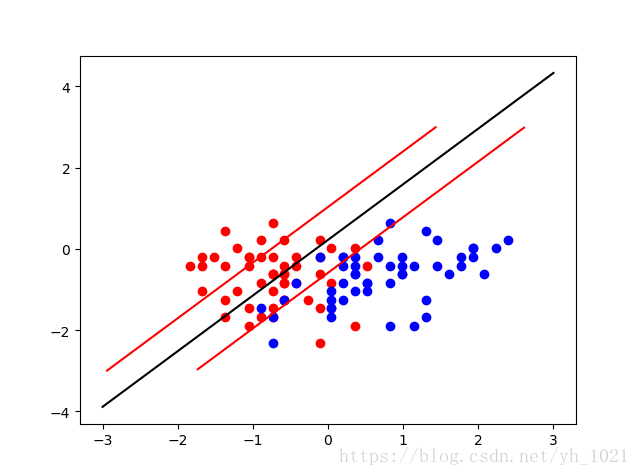
plot_svc(axis=[-3,3,-3,3])
#必须用标准化后的数据进行画图
plt.scatter(x_standard[y==0,0],x_standard[y==1,1],color='r')
plt.scatter(x_standard[y==1,0],x_standard[y==1,1],color='b')
plt.show()

当C的值取的很大（=1e11）时，容错区间较小
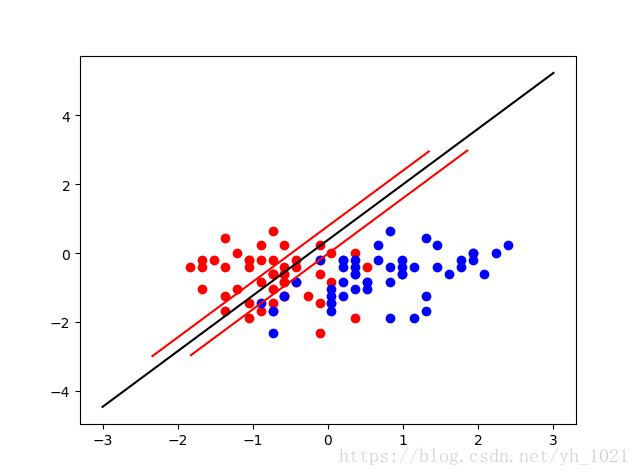
在这里插入图片描述
当C的值较小（C=0.1）时，容错空间较大
在这里插入图片描述

5、非线性SVM

（1）使用多项式特征的SVM

  • 用PolynomialFeatures生成多项式特征
  • 用StandardScaler进行数据归一化
  • 再利用LinearSVC线性SVM模型
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
#用datasets自己生成数据集
x,y=datasets.make_moons(noise=0.1,random_state=666)   #增加数据标准差，加入噪音
plt.scatter(x[y==0,0],x[y==0,1],color='r')
plt.scatter(x[y==1,0],x[y==1,1],color='b')
plt.show()

#使用多项式特征的SVM
from sklearn.preprocessing import PolynomialFeatures,StandardScaler
from sklearn.svm import  LinearSVC
from sklearn.pipeline import Pipeline

def polynomialsvc(degree,C=1.0):
    return Pipeline([
        ("poly",PolynomialFeatures(degree=degree)),
        ("std_scaler",StandardScaler()),
        ("linear_svc",LinearSVC(C=C))
    ])
poly_svc=polynomialsvc(degree=3)
poly_svc.fit(x,y)
print(poly_svc.fit(x,y))

def plot_decision_boundary(model, axis):
    x0, x1 = np.meshgrid(
        np.linspace(axis[0], axis[1], int((axis[1] - axis[0]) * 100)).reshape(-1, 1),
        np.linspace(axis[2], axis[3], int((axis[3] - axis[2]) * 100)).reshape(-1, 1)
    )
    X_new = np.c_[x0.ravel(), x1.ravel()]

    y_predict = model.predict(X_new)
    zz = y_predict.reshape(x0.shape)

    from matplotlib.colors import  ListedColormap
    custom_map=ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
    plt.contourf(x0,x1,zz,linewidth=5,cmap=custom_map)

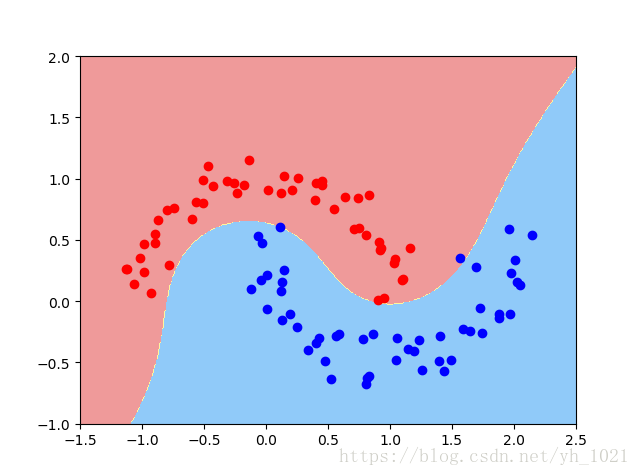
plot_decision_boundary(poly_svc,axis=[-1.5,2.5,-1,2])
plt.scatter(x[y==0,0],x[y==0,1],color='r')
plt.scatter(x[y==1,0],x[y==1,1],color='b')
plt.show()

在这里插入图片描述

（2）使用多项式核函数的SVM

  • 对数据进行归一化
  • 利用核函数SVC(kernel=‘poly’, degree=degree, C=C) （自动多项式化）
from sklearn.svm import SVC
def PolynominalKernelSVC(degree,C=1.0):
    return Pipeline([
        ("sed_scaler",StandardScaler()),
        ("kernel_svc",SVC(kernel='poly'))
    ])
poly_kernel_svc=PolynominalKernelSVC(degree=3)
poly_kernel_svc.fit(x,y)
def plot_decision_boundary(model, axis):
    x0, x1 = np.meshgrid(
        np.linspace(axis[0], axis[1], int((axis[1] - axis[0]) * 100)).reshape(-1, 1),
        np.linspace(axis[2], axis[3], int((axis[3] - axis[2]) * 100)).reshape(-1, 1)
    )
    X_new = np.c_[x0.ravel(), x1.ravel()]
    y_predict = model.predict(X_new)
    zz = y_predict.reshape(x0.shape)
    from matplotlib.colors import  ListedColormap
    custom_map=ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
    plt.contourf(x0,x1,zz,linewidth=5,cmap=custom_map)
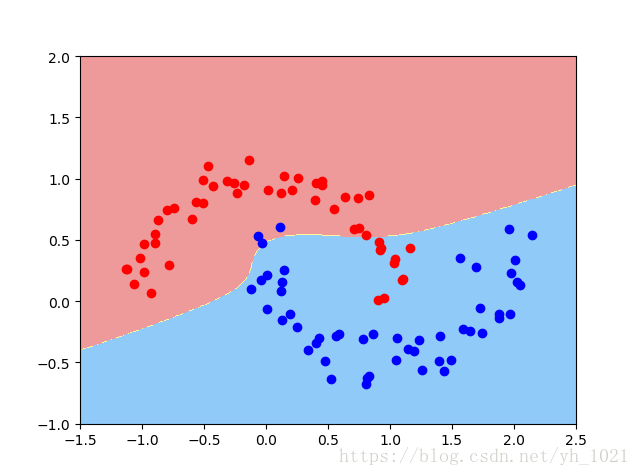
plot_decision_boundary(poly_kernel_svc,axis=[-1.5,2.5,-1,2])
plt.scatter(x[y==0,0],x[y==0,1],color='r')
plt.scatter(x[y==1,0],x[y==1,1],color='b')
plt.show()

在这里插入图片描述

多项式核函数：K(x,y)=(x⋅y+c)dK\left ( x,y \right )=\left ( x\cdot y+c \right )^{d}K(x,y)=(x⋅y+c)d
线性核函数：K(x,y)=x⋅yK\left ( x,y \right )=x\cdot yK(x,y)=x⋅y
高斯核函数：K(x,y)=e−γ∥x−y∥2K\left ( x,y \right )=e^{-\gamma\left \| x-y \right \|^{2} }K(x,y)=e−γ∥x−y∥2

（3）高斯核函数以及sklearn实现
K(x,y)=e−γ∥x−y∥2K\left ( x,y \right )=e^{-\gamma\left \| x-y \right \|^{2} }K(x,y)=e−γ∥x−y∥2
在高斯函数中，gamma越大，高斯分布越窄，gamma越小，高斯分布越宽

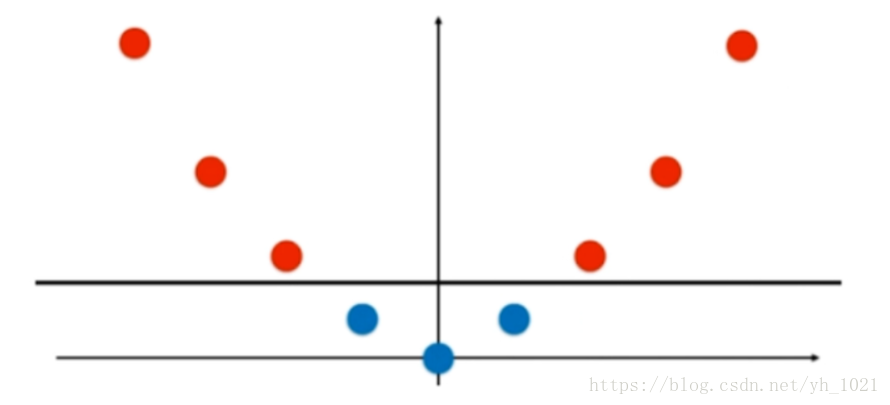
依靠升维使得原本线性不可分的数据线性可分。
假设有两类数据，分部在x轴上，如图所示这组数据是线性不可分的，即无法用直线将红和蓝分开。
在这里插入图片描述
但是将数据升维，增加一个y轴的维度（=x2x^{2}x2），数据就变得线性可分了。
在这里插入图片描述
将高斯核函数K(x,y)=e−γ∥x−y∥2K\left ( x,y \right )=e^{-\gamma\left \| x-y \right \|^{2} }K(x,y)=e−γ∥x−y∥2中的y固定为l1和l2,把一维的数据坐标x变成二维的坐标(e−γ∥x−l1∥2,e−γ∥x−l2∥2)\left ( e^{-\gamma \left \| x-l_{1} \right \|^{2}},e^{-\gamma \left \| x-l_{2} \right \|^{2}} \right )(e−γ∥x−l1​∥2,e−γ∥x−l2​∥2)
在这里插入图片描述

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
#用datasets自己生成数据集
x,y=datasets.make_moons(noise=0.1,random_state=666)   #增加数据标准差，加入噪音
plt.scatter(x[y==0,0],x[y==0,1],color='r')
plt.scatter(x[y==1,0],x[y==1,1],color='b')
plt.show()

#用sklearn中的高斯核
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline
from sklearn.svm import SVC

def RBFkernelSVC(gamma=1.0):
    return Pipeline([
        ("std_scaler",StandardScaler()),
        ("svc",SVC(kernel="rbf",gamma=gamma))
    ])
svc=RBFkernelSVC(gamma=1.0)
svc.fit(x,y)

def plot_decision_boundary(model, axis):
    x0, x1 = np.meshgrid(
        np.linspace(axis[0], axis[1], int((axis[1] - axis[0]) * 100)).reshape(-1, 1),
        np.linspace(axis[2], axis[3], int((axis[3] - axis[2]) * 100)).reshape(-1, 1)
    )
    X_new = np.c_[x0.ravel(), x1.ravel()]

    y_predict = model.predict(X_new)
    zz = y_predict.reshape(x0.shape)

    from matplotlib.colors import  ListedColormap
    custom_map=ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
    plt.contourf(x0,x1,zz,linewidth=5,cmap=custom_map)

plot_decision_boundary(svc,axis=[-1.5,2.5,-1,2])
plt.scatter(x[y==0,0],x[y==0,1],color='r')
plt.scatter(x[y==1,0],x[y==1,1],color='b')
plt.show()

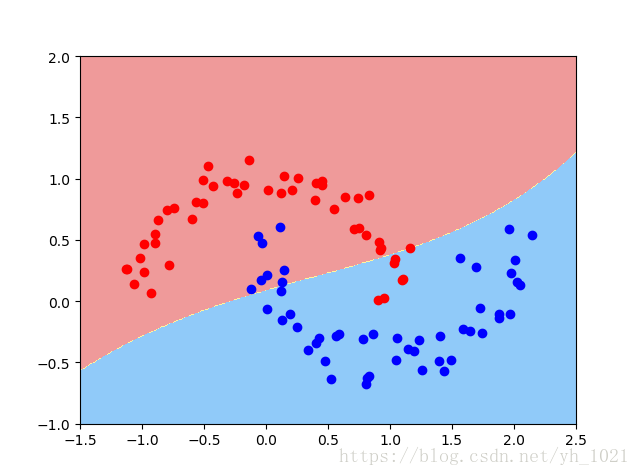
利用rbf内核，gamma取值为1的时候画出决策边界
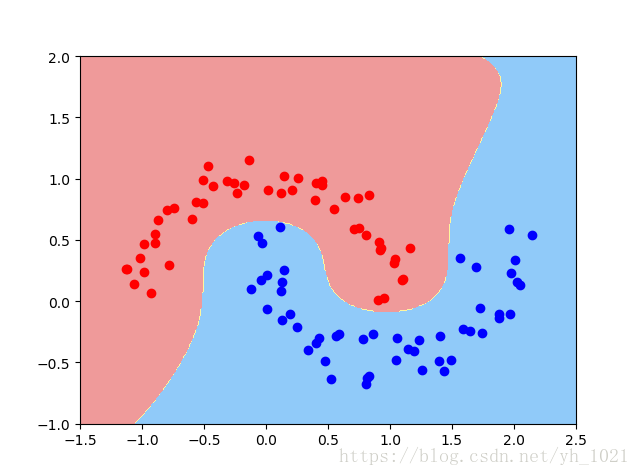
在这里插入图片描述
当gamma=100时（因为gamma越大，高斯分布的范围越窄）
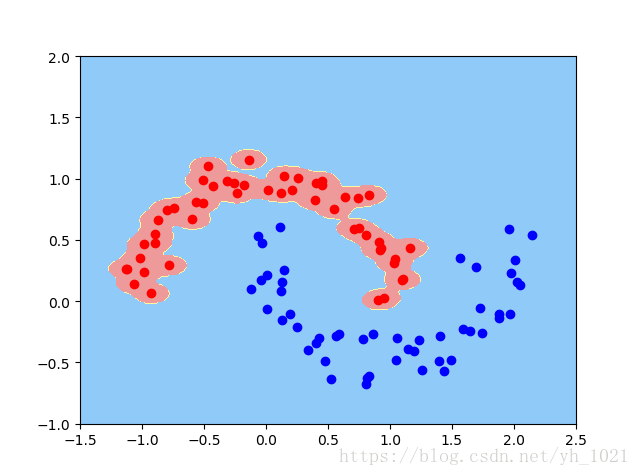
在这里插入图片描述
当gamma=0.1时
在这里插入图片描述
可以看出，当gamma值越大，高斯分布的中心范围越窄，也就是以每一个点为中心周边围绕的区域变小，当然这样的gamma值使得模型过拟合了（泛化能力低）；当gamma值很小，高斯分布的中心范围就会变得很大，每一个点的周边范围也会变得很大，如上图所示分界线近似于一条直线，这也就变成了欠拟合。
从另一个角度来说，gamma影响着模型的复杂度，gamma值越小，模型复杂度越小（欠拟合），gamma值越大，模型负责度越大（过拟合）。

6、用SVM实现回归问题

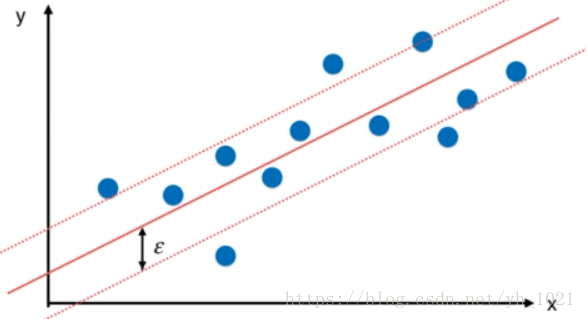
在分类任务中，我们利用了决策边界直线进行分割，并且得到了使得margin区域最大时的上下边界，在这个边界中不允许有数据点存在。而在回归问题中，我们也可以使用上下边界的概念，在得到拟合曲线之后，我们定义距离拟合曲线margin（ϵ\epsilonϵ）的两条直线为上下边界，与分类问题相反，在上下边界中包含的数据点的个数越多越好。
在这里插入图片描述

from sklearn import datasets

boston=datasets.load_boston()
x=boston.data
y=boston.target

from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test=train_test_split(x,y,random_state=666)

#使用svm中的回归函数
from sklearn.svm import LinearSVR
from sklearn.svm import SVR
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline

def standardLinearSVR(epsilon=0.1):
    return Pipeline([
        ("std_scaler",StandardScaler()),
        ("linearSVR",LinearSVR(epsilon=epsilon))
    ])
svr=standardLinearSVR()
svr.fit(x_train,y_train)
print(svr.score(x_test,y_test))

可以使用LinearSVR也可以使用SVR，使用LinearSVR时可以改变epsilon的值，C的值；使用SVR时可以改变的超参数有核函数，可以使用高斯核，可以改变gamma的值等。可以通过改变各种超参数，或者使用交叉验证的方式，来提高精确度。

yh_1021
关注
[网络安全自学篇] 十.论文之基于机器学习算法的主机恶意代码
杨秀璋的专栏
09-15 1万+
这是作者的系列网络安全自学教程，主要是关于网安工具和实践操作的在线笔记，特分享出来与博友共勉，希望您们喜欢，一起进步。本篇文章，作者将分享两篇论文，机器学习是如何运用到恶意代码攻击中的，并谈谈自己的理解，后续深入研究尝试分享相关实验，目前还是小白一只。基础性文章，希望对初学者有帮助，大神请飘过，谢谢各位看官！
支持向量机-SVM
网瘾少年康复中心
03-07 3494
小白理解的SVM
支持向量机（svm）
GGBOY1312313的博客
06-11 824
支持向量机（Support Vector Machine，简称SVM）是一种广泛应用于分类和回归分析的监督学习算法。其基本原理是通过在特征空间中找到一个最优的超平面，将不同类别的数据点分隔开。在二分类问题中，SVM的目标是找到一个能够将两类数据点分隔开的超平面，使得两侧距离最近的数据点到超平面的距离（即间隔）最大。这些最靠近超平面的数据点被称为支持向量。超平面的选择不仅要使得间隔最大，还要满足不同类别的数据点被正确分类，即位于超平面两侧的点应被分到不同的类别。
支持向量机（SVM算法）
m0_62064241的博客
07-10 8887
概念;支持向量机，英文全称“Support Vector Machines”（简称 SVM），它是机器学习中最常用的一种“分类算法”。SVM 是一种非常优雅的算法，有着非常完善的数学理论基础，其预测效果，在众多机器学习模型中可谓“出类拔萃”。在深度学习没有普及之前，“支持向量机”可以称的上是传统机器学习中的“霸主”，下面我们将介绍本节的主人公——支持向量机（SVM）。支持向量机是有监督学习中最有影响力的机器学习算法之一，该算法的诞生可追溯至上世纪 60 年代， 前苏联学者 Vapnik 在解决模式识别问题时
支持向量机（SVM）
Above the cloud
09-12 9874
SVM，中文名叫支持向量机。 在深度学习出现以前，它是数据挖掘的宠儿，SVM被认为机器学习近十几年最成功,表现最好的算法； SVM具有十分完整的数据理论证明，但同时理论也相当复杂。 SVM既可以用于回归也可以用于分类问题。 SVM的英文全称是Support Vector Machines，我们叫它支持向量机。支持向量机是我们用于分类的一种算法。让我们以一个小故事的形式，开启我们的SVM之旅吧。 在很久以前的情人节，一位大侠要去救他的爱人，但天空中的魔鬼和他玩了一个游戏。魔鬼在桌子上似乎有规律放了两种颜色的球
KNN及影响其算法性能的优化（交叉验证、是否过拟合等）——自学第二篇
热门推荐
yh_1021的博客
09-16 1万+
1、KNN(K近邻） 如图所示为每一个病人的肿瘤大小与其发现肿瘤的时间的关系，以此来判断肿瘤是否为恶性，其中恶性为蓝色，良性为红色，如果新来的病人为绿色的，需要用knn判断是否为恶性。 若k值取3，则找出之前数据中的点离新的数据点的距离最近的三个点，再分别将这三个点进行投票，若三个点中蓝色的居多，则新的点也为蓝色（恶性），反之则为红色（良性）。 上图所示离绿色点最近的三个点中，有两个...
模式分类课程完整PPT详解：从贝叶斯到支持向量机
“支持向量机及其应用”这一专题PPT深入剖析了现代机器学习中最具影响力的分类器之一——支持向量机（SVM）。SVM基于结构风险最小化原则，通过寻找最大间隔超平面实现强泛化能力。课程详细推导了硬间隔与软间隔SVM的...
1.1 从图灵机到GPT，人工智能经历了什么？——《带你自学大语言模型》系列
陌北有棵树的博客
06-23 1564
本节主要从发展史的角度，梳理自AI诞生起经历了哪些阶段，从而让我们更清晰地认识到，当下我们是处在哪个位置？ 虽然今天正处于本轮AI的应用爆发初期，大家更感兴趣的是如何基于大模型做应用开发，但我仍然希望读者愿意花十几分钟的时间，去探索这个领域是如何走到今天的。对当下是否真的走在了”正确“的道路上，有自己辨证且深入的思考。与其杞人忧天 AI 产生智慧，我们更应该担心自己因为人云亦云从而失去智慧。
灰狼优化算法优化SVM参数实现光谱预测与分类
灰狼优化算法（Grey Wolf Optimizer, GWO）在支持向量机（Support Vector Machine, SVM）参数优化中的应用，是当前机器学习领域中一个极具研究价值和实际意义的技术方向。该方法通过模拟自然界中灰狼群体的社会等级...
支持向量机(SVM)
最新发布
2401_87608917的博客
05-08 1880
支持向量机是一种监督学习算法，最初由统计学家Vladimir Vapnik在20世纪90年代提出。它的核心思想可以简单概括为：​​找到一个最优的超平面，将不同类别的数据点尽可能远地分开​​。​​超平面​​：在二维空间中是一条线，三维中是一个平面，更高维度中是超平面​​最大间隔​​：SVM试图找到使两类数据点间隔（margin）最大的超平面想象一下，你需要用一根棍子将苹果和橘子分开。粗心的方式可能随便一放就完事，但SVM会选择最中间的位置放置棍子，这样即使新来的苹果或橘子出现轻微偏移，依然能被正确分类。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值