作业二

最新推荐文章于 2024-06-21 19:20:27 发布

原创最新推荐文章于 2024-06-21 19:20:27 发布 · 417 阅读

0 ·

CC 4.0 BY-SA版权

计量作业专栏收录该内容

0 篇文章

订阅专栏

第一题：

（1）

> fm=lm(exp~income,data=consumption[25:200,])
> fm

Call:
        lm(formula = exp ~ income, data = consumption[25:200, ])

Coefficients:
        (Intercept)       income  
7550.2970       0.8567

故可支配收入的边际消费倾向为0.8567

（2）

>b=residuals(fm)
> plot(b~consumption$year[25:200],xlab="时间",ylab="resduals",main="残差的散点图")
> abline(h=0)

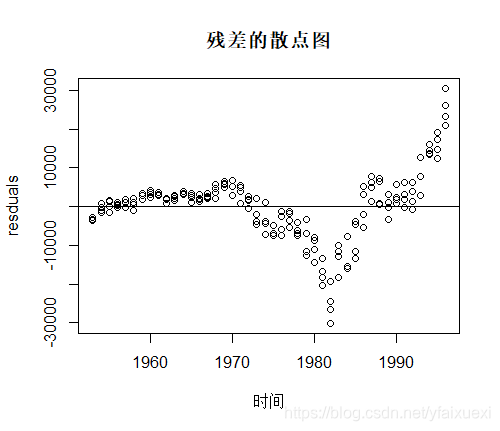
由残差的散点图可以看出，残差并不均匀的分布于0的两边，故消费函数的模型没有被很好的说明

（3）

> consumtion.simulate=numeric(0)
> e=rnorm(1000,mean=0,sd=sd(b))
> for(i in 25:200){
+     consumtion.simulate[i]=fm$coefficients[1]+fm$coefficients[2]*consumption$income[i]+e[i]
+ }
> consumtion.simulate

 [1]        NA        NA        NA        NA        NA        NA        NA        NA        NA        NA        NA        NA        NA
 [14]        NA        NA        NA        NA        NA        NA        NA        NA        NA        NA        NA  67602.38  85361.77
 [27]  91099.13  70015.95  60661.14  55368.01  73888.95  68236.34  83866.94  71897.67  75680.88  78062.76  70394.12  84843.30  91000.17
 [40]  87677.12  74300.04  81240.22  92586.31  83171.57 104099.65  97171.95  94383.86  80940.79  92911.47  88645.74  87371.14 104732.63
 [53]  83170.00  88732.84  95637.48 108196.25  97111.01  98903.78 103386.57  85517.69 100632.89 109468.58  93445.84 104913.64 115803.67
 [66] 112661.08 114327.32 100433.40 106786.50 105092.67 106094.08 111246.33 112058.63 125349.80 121831.10 121320.89 113496.89 129664.88
 [79] 129077.53 141532.35 156271.87 134235.05 133661.62 125898.42 160840.96 130739.91 127310.58 149179.79 153186.93 141285.96 142481.44
 [92] 154480.87 154751.36 162861.08 139387.68 158845.07 150828.99 161372.45 167336.35 177637.52 169567.68 180572.40 157809.60 191593.46
[105] 189344.36 187312.54 199243.93 188721.23 208851.13 205626.25 198539.07 205412.41 200494.46 225353.16 220274.46 225245.26 226412.29
[118] 240965.72 223026.73 233325.44 237005.07 237281.97 250961.51 228358.83 250932.17 253592.84 230730.16 255180.34 249588.10 248038.71
[131] 267452.41 264014.04 248605.48 264046.10 252463.65 257183.41 280553.85 275228.67 287612.17 282627.58 273259.42 291749.13 263067.30
[144] 265522.83 274601.96 262936.90 276549.90 272589.96 284995.22 286564.34 283023.15 299163.32 286280.12 306082.98 290402.80 302817.12
[157] 296547.00 293310.55 290185.30 300831.89 299587.42 301168.93 303105.27 297884.62 309939.98 317422.30 337479.84 329209.80 322125.42
[170] 336058.18 330487.34 321292.91 349703.02 329182.67 344560.38 345304.33 315574.14 314761.65 325225.87 339137.94 324060.50 331547.16
[183] 348333.15 323140.18 339415.36 335924.37 353086.22 324917.34 341164.77 333653.74 346251.10 339287.65 346000.25 346904.47 346162.92
[196] 365042.41 335132.85 355920.85 343495.43 360925.92

（4）

> fm1=lm(consumtion.simulate[25:200]~consumption$income[25:200])
> fm1

Call:
lm(formula = consumtion.simulate[25:200] ~ consumption$income[25:200])

Coefficients:
               (Intercept)  consumption$income[25:200]  
                 4447.8737                      0.8692

估计参数和原数据的估计参数明显不同，因为之前的模型中误差并不符合正态分布，而我们现在的误差是符合正态分布的。

（5）

> c=residuals(fm1)
> plot(consumption$year[25:200],c,xlab="时间",ylab="残差",main="残差散点图")
> abline(h=0)

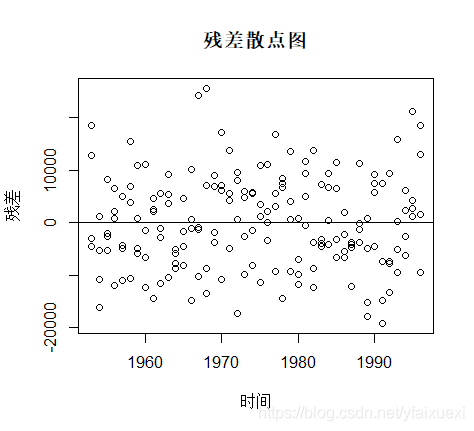
该残差散点图看起来与之前的残差散点图明显不同。

第二题

（1）

tbrate.lm <- lm (`delta r(t)`~1+`delta r(t-1)`+`delta r(t-2)`+`pi(t-1)`+`delta y(t-1)`,tbrate)

> summary(tbrate.lm)
Call:
        lm(formula = `delta r(t)` ~ 1 + `delta r(t-1)` + `delta r(t-2)` + 
                   `pi(t-1)` + `delta y(t-1)`, data = tbrate)

Residuals:
        Min      1Q  Median      3Q     Max 
-3.6601 -0.3893 -0.0103  0.4276  3.9350 

Coefficients:
        Estimate Std. Error t value Pr(>|t|)   
(Intercept)    -0.23194    0.12561  -1.846  0.06647 . 
`delta r(t-1)`  0.23746    0.07407   3.206  0.00159 **
        `delta r(t-2)` -0.15402    0.07254  -2.123  0.03510 * 
        `pi(t-1)`       0.01606    0.02003   0.802  0.42367   
`delta y(t-1)` 18.38074    5.75892   3.192  0.00167 **
        ---
        Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.8911 on 180 degrees of freedom
(3 observations deleted due to missingness)
Multiple R-squared:  0.1344,	Adjusted R-squared:  0.1152 
F-statistic: 6.988 on 4 and 180 DF,  p-value: 2.984e-05

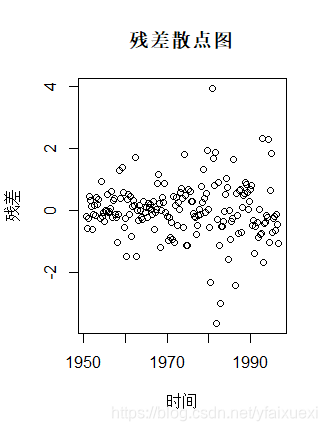
> b=residuals(tbrate.lm)
> t<-seq(1950.75,1996.75,0.25)
> plot(t,b,xlab="时间",ylab="残差",main="残差散点图")
>abline(h=0)

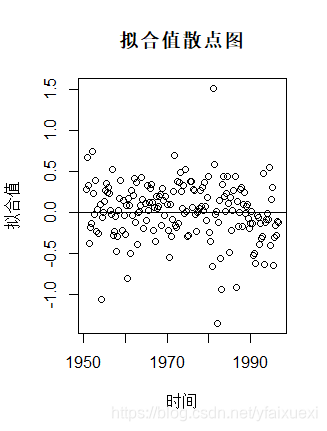
> plot(t,tbrate.lm$fitted.values,xlab="时间",ylab="拟合值",main="拟合值散点图")
> abline(h=0)

> lm2<-lm(b~tbrate.lm$fitted.values)
> summary(lm2)

Call:
        lm(formula = b ~ tbrate.lm$fitted.values)

Residuals:
        Min      1Q  Median      3Q     Max 
-3.6601 -0.3893 -0.0103  0.4276  3.9350 

Coefficients:
        Estimate Std. Error t value Pr(>|t|)
(Intercept)              2.218e-17  6.503e-02       0        1
tbrate.lm$fitted.values -5.891e-16  1.876e-01       0        1

Residual standard error: 0.8838 on 183 degrees of freedom
Multiple R-squared:  4.048e-32,	Adjusted R-squared:  -0.005464 
F-statistic: 7.408e-30 on 1 and 183 DF,  p-value: 1

将残差对拟合值做回归，可以看出回归的调整拟合优度接近于0，且t-value=0.说明残差不能对拟合值进行拟合。

> lm3<-lm(tbrate.lm$fitted.values~b)
> summary(lm3)

Call:
        lm(formula = tbrate.lm$fitted.values ~ b)

Residuals:
        Min       1Q   Median       3Q      Max 
-1.37411 -0.18022  0.01318  0.22632  1.50550 

Coefficients:
        Estimate Std. Error t value Pr(>|t|)
(Intercept)  1.339e-02  2.561e-02   0.523    0.602
b           -1.021e-16  2.913e-02   0.000    1.000

Residual standard error: 0.3483 on 183 degrees of freedom
Multiple R-squared:  6.272e-32,	Adjusted R-squared:  -0.005464 
F-statistic: 1.148e-29 on 1 and 183 DF,  p-value: 1

将拟合值对残差做回归，调整拟合优度接近0，且t-value接近于0，故拟合值中不存在残差可以解释的部分。

（2）

> lm4<- lm (`delta r(t)`~1+`delta r(t-1)`+`delta r(t-2)`+`delta y(t-1)`,tbrate)
> ethat=residuals(lm4)
> lm5<- lm (`pi(t-1)`~1+`delta r(t-1)`+`delta r(t-2)`+`delta y(t-1)`,tbrate）
> vthat=residuals(lm5)
> lm6<-lm(ethat~vthat)
 

> summary(lm6)

Call:
lm(formula = ethat ~ vthat)

Residuals:
    Min      1Q  Median      3Q     Max 
-3.6601 -0.3893 -0.0103  0.4276  3.9350 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.288e-17  6.498e-02   0.000     1.00
vthat       1.606e-02  1.987e-02   0.809     0.42

Residual standard error: 0.8838 on 183 degrees of freedom
Multiple R-squared:  0.00356,	Adjusted R-squared:  -0.001885 
F-statistic: 0.6538 on 1 and 183 DF,  p-value: 0.4198

R-squared接近于0，t值也接近于0，且不显著，说明ethat不能与vthat进行回归，ethat中不存在vthat能够解释的部分。也就是说，对于pi(t-1)和delta r(t)，在排除delta r(t-1)，delta r(t-2)，delta y(t-1)的解释部分后，pi(t-1)中不存在能解释delta r(t)的部分，这正好解释了回归方程(1)中pi(t-1)的估计参数不显著，因为其能解释的已经被其他三者覆盖了。

（3）

ht <- hatvalues(tbrate.lm)
p <- length(tbrate.lm$coefficients)
n <- length(tbrate.lm$fitted.values)
plot(t,ht,xlab = '年',main = '高杠杆点')
abline(h = 3*p/n,col = 2,lty = 4 , lwd = 2)

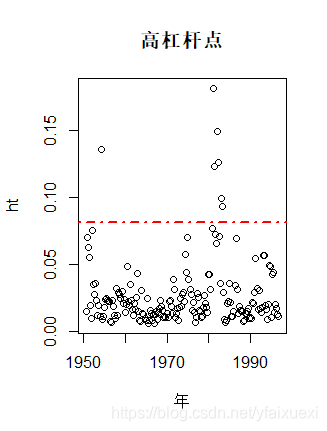
如上图所示，虚线以上为高杠杆点。