一、矩阵的引入
显然,矩阵的概念应该从方程组的概念引入。例如:
2x−y=02x−y=0
−x+2y=3−x+2y=3
其矩阵形式为:
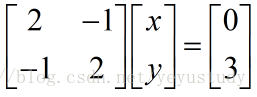
接下来介绍两种不同分析矩阵的方法:
行图像:实质是将矩阵按行进行思考,例如上例中的两个方程,将其在坐标轴上画出图像,其交点即为方程组的解
列图像:实质是将矩阵按列进行思考,即这种形式:
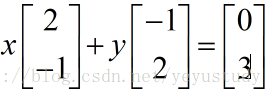
即向量的线性组合,只要经过线性组合能得到的右边的向量,则解必然能够找到。
二、消元
通过主元来进行消元,例如:

需要注意的是,主元永远不会是0,如果最后一个主元是零,意味着消元失效。
三、矩阵的乘法
矩阵的乘法可以看做向量对矩阵的操作,以这种思想来看,就容易解释为什么行变换是左乘矩阵,列变换是右乘矩阵。因此,矩阵的乘法不能改变顺序
四、矩阵的逆
关于矩阵逆的一种解释,如果存在非零向量X使得AX=0,则A肯定是奇异不可逆的。如果可逆,最终会推得X为0,矛盾
求矩阵的逆可使用高斯-若尔当消元法
线性代数(一)
最新推荐文章于 2018-10-08 00:08:56 发布
























 3724
3724

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








