一、关联分析概述
大型超市有海量的交易数据,作为精明的商家肯定不会放弃对这些海量数据的应用,他们希望通过对这些交易数据的分析,了解顾客的购买行为。我们可以通过聚类算法寻找购买相似物品的人群,从而为特定人群提供更具个性化的服务。但是对于超市来讲,更有价值的是找出商品之间的隐藏关联,从而可以用于商品定价、市场促销、存货管理等一系列环节,来增加营业收入。那如何从这种海量而又繁杂的交易数据中找出商品之间的关联呢?当然,你可以使用穷举法,但是这是一种十分耗时且计算代价高的笨方法,所以需要用更智能的方法在合理的时间范围内找到答案。因此,关联分析就此诞生了。
1. 关联分析
关联分析(association analysis)是一种在大规模数据集中寻找有趣关系的非监督学习算法。这种关系可以有两种形式:频繁项集或者关联规则。频繁项集(frequent item sets)是经常出现在一块的物品的集合,关联规则(association rules)暗示两种物品之间可能存在很强的关系。
关联分析的一个典型例子是购物篮分析。下面我们一起来看一个简单例子。
| 交易号码 | 商品 |
|---|---|
| 001 | 豆奶,莴苣 |
| 002 | 莴苣,尿布,啤酒,甜菜 |
| 003 | 豆奶,尿布,啤酒,橙汁 |
| 004 | 莴苣,豆奶,尿布,啤酒 |
| 005 | 莴苣,豆奶,尿布,橙汁 |
交易号码代表交易流水号,商品代表一个顾客一次购买的全部商品。
- 事务:每一条交易称为一个事务。例如,在这个例子中包含了5个事务。
- 项:交易的每一个物品称为一个项,例如豆奶、尿布等。
- 项集:包含零个或者多个项的集合叫做项集,例如 {豆奶,莴苣}。
- k-项集:包含k个项的项集叫做k-项集。例如 {豆奶} 叫做1-项集,{豆奶,尿布,啤酒} 叫做3-项集。前件和后件:对于规则{尿布}→{啤酒},{尿布} 叫做前件,{啤酒} 叫做后件。
2. 频繁项集的评估标准
频繁项集是经常出现在一块的物品的集合,那么问题就来了:第一,当数据量非常大的时候,我们无法凭肉眼找出经 常出现在一起的物品,这就催生了关联规则挖掘算法,比如 Apriori、PrefixSpan、CBA 等。第二是我们缺乏一个频繁项集的标准。比如10条记录,里面A和B同时出现了三次,那么我们能不能说A和B一起构成频繁项集呢?因此我们需要一个评估频繁项集的标准。
常用的频繁项集的评估标准有支持度,置信度和提升度三个。
3.1 支持度
支持度就是几个关联的数据在数据集中出现的次数占总数据集的比重。或者说几个数据关联出现的概率。如果我们有 两个想分析关联性的数据X和Y,则对应的支持度为:
S
u
p
p
o
r
t
(
X
,
Y
)
=
P
(
X
Y
)
=
n
u
m
b
e
r
(
X
Y
)
n
u
m
(
A
l
l
S
a
m
p
l
e
s
)
Support(X,Y) = P(XY) = \frac{number(XY)}{num(AllSamples)}
Support(X,Y)=P(XY)=num(AllSamples)number(XY)
比如上面例子中,在5条交易记录中{尿布, 啤酒}总共出现了3次,所以:
S
u
p
p
o
r
t
(
尿
布
,
啤
酒
)
=
3
5
Support(尿布,啤酒) = \frac{3}{5}
Support(尿布,啤酒)=53
以此类推,如果我们有三个想分析关联性的数据X,Y和Z,则对应的支持度为:
S
u
p
p
o
r
t
(
X
,
Y
,
Z
)
=
P
(
X
Y
Z
)
=
n
u
m
b
e
r
(
X
Y
Z
)
n
u
m
(
A
l
l
S
a
m
p
l
e
s
)
Support(X,Y,Z) = P(XYZ) = \frac{number(XYZ)}{num(AllSamples)}
Support(X,Y,Z)=P(XYZ)=num(AllSamples)number(XYZ)
一般来说,支持度高的数据不一定构成频繁项集,但是支持度太低的数据肯定不构成频繁项集。 另外,支持度是针对项集来说的,因此,可以定义一个最小支持度,而只保留满足最小支持度的项集,起到一个项集过滤的作用。
3.2 置信度
置信度体现了一个数据出现后,另一个数据出现的概率,或者说数据的条件概率。如果我们有两个想分析关联性的数 据X和Y,X对Y的置信度为:
C
o
n
f
i
d
e
n
c
e
(
X
−
>
Y
)
=
P
(
Y
∣
X
)
=
P
(
X
Y
)
P
(
X
)
Confidence(X->Y) = P(Y|X) = \frac{P(XY)}{P(X)}
Confidence(X−>Y)=P(Y∣X)=P(X)P(XY)
比如上面例子中,莴苣对豆奶的置信度=豆奶和莴苣同时出现的概率/莴苣出现的概率,则有
P
(
豆
奶
∗
莴
苣
)
=
3
5
P
(
豆
奶
∗
莴
苣
)
=
3
5
C
o
n
f
i
d
e
n
c
e
(
莴
苣
−
>
豆
奶
)
=
P
(
豆
奶
∗
莴
苣
)
P
(
莴
苣
)
=
0.6
0.8
=
0.75
P(豆奶*莴苣) = \frac{3}{5} \\ P(豆奶*莴苣) = \frac{3}{5} \\Confidence(莴苣->豆奶) = \frac{P(豆奶*莴苣)}{P(莴苣)} = \frac{0.6}{0.8} = 0.75
P(豆奶∗莴苣)=53P(豆奶∗莴苣)=53Confidence(莴苣−>豆奶)=P(莴苣)P(豆奶∗莴苣)=0.80.6=0.75
也可以以此类推到多个数据的关联置信度,比如对于三个数据X,Y,Z,则Y和Z对于X的置信度为:
C
o
n
f
i
d
e
n
c
e
(
Y
Z
−
>
X
)
=
P
(
X
∣
Y
Z
)
=
P
(
X
Y
Z
)
P
(
Y
Z
)
Confidence(YZ->X) = P(X|YZ) = \frac{P(XYZ)}{P(YZ)}
Confidence(YZ−>X)=P(X∣YZ)=P(YZ)P(XYZ)
为什么使用支持度和置信度?支持度是一种重要度量,因为支持度很低的规则可能只是偶然出现。从商务角度来看, 低支持度的规则多半也是无意义的,因为对顾客很少同时购买的商品进行促销可能并无益处。因此,支持度通常用来 删去那些无意义的规则。此外,支持度还具有一种期望的性质,可以用于关联规则的有效发现。
另一方面,置信度度量通过规则进行推理具有可靠性。对于给定的规则X→Y,置信度越高,Y在包含X的事务中出现的 可能性就越大。置信度也可以估计Y在给定X下的条件概率。
同时,应当小心解释关联分析的结果。由关联规则作出的推论并不必然蕴涵因果关系。它只表示规则前件和后件同时 出现的一种概率。
2.3 提升度
现有的关联规则的挖掘算法需要使⽤⽀持度和置信度来除去没有意义的模式。⽀持度的缺点在于许多潜在的有意义的模式由于包含⽀持度小的项而被删去,置信度的缺点更加微妙,用下面的例子最适于说明。
| 咖啡 | 不喝咖啡 | ||
|---|---|---|---|
| 茶 | 150 | 50 | 200 |
| 不喝茶 | 650 | 150 | 800 |
| 800 | 200 | 1000 |
可以使⽤表中给出的信息来评估关联规则{茶}→{咖啡}。猛⼀看,似乎喜欢喝茶的⼈也喜欢喝咖啡,因为该规则的支 持度(15%)和置信度(75%)都相当的高。这个推论也许是可以接受的,但是所有的⼈中,不管他是否喝茶,喝咖啡的⼈的比例为80%,⽽喝咖啡的饮茶者却只占75%。也就是说,⼀个人如果喝茶,则他喝咖啡的可能性由80%减到了75%。因此,尽管规则{茶}→{咖啡}有很高的置信度,但是它却是⼀个误导。所以说,置信度的缺陷在于该度量忽略了规则后件中项集的⽀持度。
茶与咖啡的例⼦表明,由于置信度度量忽略了规则后件中出现的项集的⽀持度,高置信度的规则有时可能出现误导。 解决这个问题的⼀种⽅法是使⽤称作提升度(lift)的度量:
l
i
f
t
(
X
−
>
Y
)
=
C
o
n
f
i
d
e
n
c
e
(
X
−
>
Y
)
S
u
p
p
o
r
t
(
Y
)
=
C
o
n
f
i
d
e
n
c
e
(
X
−
>
Y
)
P
(
Y
)
lift(X->Y) = \frac{Confidence(X->Y)}{Support(Y)} = \frac{Confidence(X->Y)}{P(Y)}
lift(X−>Y)=Support(Y)Confidence(X−>Y)=P(Y)Confidence(X−>Y)
提升度体先了X和Y之间的关联关系, 提升度大于1则 是有效的强关联规则, 提升度小于等于1则 是无效的强关联规则 。一个特殊的情况,如果X和Y独立,则有,因为此时 。
那我们计算一下{茶}→{咖啡}的提升度:
l
i
f
t
(
茶
−
>
咖
啡
)
=
P
(
咖
啡
∣
茶
)
P
(
咖
啡
)
=
0.75
0.8
=
0.94
lift(茶->咖啡) = \frac{P(咖啡|茶)}{P(咖啡)} = \frac{0.75}{0.8} = 0.94
lift(茶−>咖啡)=P(咖啡)P(咖啡∣茶)=0.80.75=0.94
一般来说,要选择一个数据集合中的频繁数据集,则需要自定义评估标准。最常用的评估标准是用自定义的支持度, 或者是自定义支持度和置信度的一个组合。
3. 关联规则的发现
给定事务的集合T,关联规则发现是指找出支持度大于等于 并且置信度大于等于 的所有规则,其中和 是对应的支持度和置信度阈值。挖掘关联规则的一种原始方法是:计算每个可能规则的支持度 和置信度。但是这种方法的代价很高,令人望而却步,因为可以从数据集提取的规则的数目达指数级。更具体地说, 从包含d个项的数据集提取的可能规则的总数为:
R
=
3
d
−
2
d
+
1
+
1
R = 3^d - 2^{d+1}+1
R=3d−2d+1+1
【公式证明过程】可参考:https://blog.youkuaiyun.com/wxbmelisky/article/details/48268833
对于前面的小例子,里面一共有6中商品,提取的可能规则数为:
3
6
−
2
7
+
1
=
602
3^6-2^7+1 = 602
36−27+1=602 ,也就是说对于只有6种商品的小数据集都需要计算602条规则的支持度和置信度。使用minsup= 20%和minconf=50%,80%以上的规则将被丢弃,使得大部分计算是无用的开销。为了避免进行不必要的计算,事先对规则剪枝,而无须计算它们的支持度和置信 度的值将是有益的。 因此,大多数关联规则挖掘算法通常采用的一种策略是,将关联规则挖掘任务分解为如下两个主要的子任务。
- 频繁项集产生:
其目标是发现满足最小支持度阈值的所有项集,这些项集称作频繁项集(frequent itemset) 。 - 规则的产生:
其目标是从上一步发现的频繁项集中提取所有高置信度的规则,这些规则称作强规则(strong rule)。
通常,频繁项集产生所需的计算开销远大于产生规则所需的计算开销。那有没有办法可以减少这种无用的计算呢?有。下面这两种方法可以降低产生频繁项集的计算复杂度:
(1)减少候选项集的数目M。
(2)减少比较次数。替代将每个候选项集与每个事务相匹配,可以使用更高级的数据结构,或者存储候选项集或者压缩数据集,来减少比较次数。
这些策略将在Apriori算法基本思想中进行讨论。
二、 Apriori算法
先验原理 : 如果一个项集是频繁的,则它的所有子集一定也是频繁的。
假设我们在经营一家商品种类并不多的杂货店,我们对那些经常在一起被购买的商品非常感兴趣。我们只有4种商 品:商品0,商品1,商品2和商品3。那么所有可能被一起购买的商品组合都有哪些?这些商品组合可能只有一种商 品,比如商品0,也可能包括两种、三种或者所有四种商品。我们并不关心某人买了两件商品0以及四件商品2的情 况,我们只关心他购买了一种或多种商品。
下图显示了物品之间所有可能的组合。为了让该图更容易懂,图中使用物品的编号0来取代物品0本身。另外,图中从 上往下的第一个集合是Ф,表示空集或不包含任何物品的集合。物品集合之间的连线表明两个或者更多集合可以组合 形成一个更大的集合。
根据先验原理,假如 {1,2,3} 是频繁项集,那么它的所有子集(下图中橘色项集)一定也是频繁的。

这个先验原理直观上并没有什么帮助,但是反过来看就有用了,也就是说如果一个项集是非频繁项集,那么它的所有 超集也是非频繁的(如下图所示)。

上图中,已知阴影项集 {2,3} 是非频繁的。利用这个知识,我们就知道项集{0,2,3} ,{1,2,3}以及{0,1,2,3}也是非频繁的。这也就是说,一旦计算出了{2,3}的支持度,知道它是非频繁的之后,就不需要再计算{0,2,3}、{1,2,3}和{0,1,2,3} 的支持度,因为我们知道这些集合不会满足我们的要求。使用该原理就可以避免项集数目的指数增长,从而在合理时间内计算出频繁项集。
三、 利用Apriori算法来发现频繁项集
关联分析的目的包括两项:发现频繁项集和发现关联规则。首先需要找到频繁项集,然后才能获得关联规则。
Apriori 算法过程

C1,C2,…,Ck分别表示1-项集,2-项集,…,k-项集;
L1,L2,…,Lk分别表示有k个数据项的频繁项集。
Scan表示数据集扫描函数。该函数起到的作用是支持度过滤,满足最小支持度的项集才留下,不满足最小支持度的项集直接舍掉。
下面我们用python代码来实现这一过程。
1、 生成候选项集
数据集扫描的伪代码如下:
对数据集中的每条交易记录transaction 对每个候选项集can:
检查can是否是transaction的子集:
如果是,增加can的计数
对每个候选项集:
如果支持度不低于最小值,则保留该项集
返回所有频繁项集列表
函数一:创建一个用于测试的简单数据集
#导入包
import pandas as pd
import numpy as np
#创建生成数据集的函数
def loadDataSet():
dataSet = [[1,3,4],[2,3,5],[1,2,3,5],[2,5]]
return dataSet
函数二:构建第一个候选集合C1
由于算法一开始是从输入数据集中提取候选项集列表,所以这里需要一个特殊的函数来处理——frozenset类型。frozenset是指被“冰冻”的集合,也就是用户不能修改他们。这里必须要用frozenset而非set类型,是因为后面我们要将这些集合作为字典键值使用。
s = set('hello') #生成集合,集合会自动去重
s.add('a') #集合允许修改
f = frozenset('hello') #创建frozenset类型,也有去重功能
f.add('a') #frozdenset类型不允许修改
该函数流程是:首先创建一个空列表,用来储存所有不重复的项值。接下来遍历数据集中所有的交易记录,对每一条 交易记录,遍历记录中的每一个项。如果该项没有在C1中出现过,那么就把它添加到C1中,这里需要注意的是,并 非简单地添加物品项,而是添加只包含该物品项的一个集合(此处用集合或者列表都可以)。循环完毕后,对整个C1进行排序并将其中每个单元素集合映射到frozenset(),最后返回frozenset的列表。
'''
函数功能: 生成一个候选集合C1
参数说明:
dataSet:原始数据集
返回: frozen形式的候选频繁项集
'''
def createC1(dataSet):
c1 = [] #候选1项集
for transaction in dataSet:
for item in transaction:
if not {item} in c1:
c1.append({item})
c1.sort()
return list(map(frozenset,c1))
C1=createC1(dataSet)
C1
'''
[frozenset({1}),
frozenset({3}),
frozenset({4}),
frozenset({2}),
frozenset({5})]
'''
- .sort()函数起到排序的作用,默认从小到大排序。
- map()是python内置的高阶函数,它接收一个函数f 和一个列表list,它的功能是把函数 f 依次作用到list 的每个元素上,得到一个新的list然后返回。
函数三:生成满足最小支持度的频繁项集L1
C1是大小为1的所有候选项集的集合,Apriori算法首先构建集合C1,然后扫描数据集来判断这些只有一个元素的项集是否满足最小支持度的要求。那些满足最低要求的项集构成集合L1。
'''
函数功能:生成满足最小支持度的频繁项集L1
参数说明:
D:原始数据
Ck:候选项集
minSupport: 最小支持度
返回:
retList:频繁项集
supportData:所有候选项集的支持度
'''
def scanD(D,Ck,minSupport):
#字典形式存放项集及其出现的次数{项集:次数}
ssCnt = {}
#每一条事务集
for tid in D:
#候选集中的每一个项集
for can in Ck:
#判断can是否是tid的子集
if can.issubset(tid):
#如果是子集则字典值加1
#get(item,num) num=>如果字典中没找到返回num,这里返回0
ssCnt[can] = ssCnt.get(can,0)+1
#数据集长度,float计算更快一点
numItems = float(len(D))
#频繁项集
retList = []
#候选项集ck的支持度字典(key候选项,value支持度)
supportData = {}
for key in ssCnt:
#计算每一个项集的支持度
support = ssCnt[key]/numItems
#将所有项集及其支持度的形式放入到supportData
supportData[key] = support
#如果满足最小支持度的要求
if supportData[key] >= minSupport:
retList.append(key)
#返回频繁项集和所有候选项集的支持度
return retList,supportData
L1,supportData = scanD(dataSet,c1,0.5)
L1,supportData

从运行结果中可以看出,设定最小支持度为0.5时,frozenset({4})支持度为0.25<0.5,就被舍弃了,没有放入到L1 中。
2、 项集迭代函数
根据前述Apriori算法工作流程,我们已经有了频繁一项集的生成函数,但是我们还缺少由频繁k项集生成候选k+1项集的函数,下面我们就来构建这个函数。构建这个函数的思路是:将不同的频繁k项集两两合并生成候选k+1项集。 在这个函数的构造过程中,有两点需要注意:
- Ck中不会放重复的项集,这样会增加计算量。也就是说在生成候选k+1项集之后需要判断,这个候选k+1项集是否已经存在Ck中,如果没有的话再把它放入Ck,反之则舍弃。
- 判断两两合并之后得到的项集是不是长度为k+1,如果是则放入Ck,反之则舍弃。
运算符| 在python中表示集合的合并,frozenset集合也可以执行合并操作,并且合并结果仍为frozenset类型。

"""
函数功能:由频繁k项集生成候选k+1项集参数说明
Lk:频繁k项集
返回:
Ck:候选k+1项集
"""
#连接操作,将频繁k项集通过拼接转化为候选k+1项集
def aprioriGen(Lk):
#用于放置候选k+1项集
ck = []
lenLk = len(Lk)
for i in range (lenLk):
for j in range(i+1,lenLk):
L1 = Lk[i]
L2 = Lk[j]
C = Lk[i] | Lk[j]
if not C in ck and (len(C) == (len(Lk[0])+1)):
ck.append(Lk[i]|Lk[j])
return ck
由前面运行结果得知L1中共有4个频繁1项集,那两两组合的话,可以得到 个候选2项集。现在我们用aprioriGen函数由频繁1项集生成候选2项集,查看运行结果:

接下来可以看一下由频繁2项集生成候选3项集,并由候选3项集生成频繁3项集的过程。在这个过程中,首先用scanD 函数根据候选2项集C2生成频繁2项集L2,再用aprioriGen函数生成候选3项集C3,之后再次使用scanD函数生成频繁3项集L3。

函数2:根据数据集和支持度,返回所有的频繁项集,以及所有项集的支持度。
'''
Apriori主函数:根据输入的数据集,返回所有频繁项集和所有项集的支持度
参数说明:
D:原始数据集
minSupport:最小支持度
返回:
L: 所有频繁项集
supportData:所有项集及其支持度
'''
def apriori(D, minSupport = 0.5):
C1 = createC1(D) #生成候选1项集
L1, supportData = scanD(D, C1, minSupport) #生成频繁1项集和支持度列表
L = [L1] #将频繁1项集放入L中k=2 #项集数,初始值设为2
while (len(L[-1]) > 0): #如果L中最后项集中的元素数不为0则持续循环
Ck = aprioriGen(L[-1]) #生成候选k项集
Lk, supK = scanD(D, Ck, minSupport) #根据候选k项集,生成频繁k项集和支持度列表supportData.update(supK) #更新支持度列表
L.append(Lk) #更新频繁项集L
k=k+1
return L, supportData
dataSet = loadDataSet()
L,supportData = apriori(dataSet,minSupport=0.5)

流程如下图:

四、 Apriori关联规则挖掘
1. 挖掘规则的流程
完成频繁项集的挖掘之后,我们就可以根据这些频繁项集来寻找关联规则了。对于频繁项集,上面给出了量化定义, 即它满足最小支持度要求。那么,对于关联规则,我们也有类似的量化方法——置信度。对于一条规则P→H的置信 度可以表示为: 。在python中,操作符|表示集合的并操作,数学上集合并的符号是
∪。
类似于频繁项集的生成,每一个频繁项集也可以生成许多条关联规则。如下图,列出了频繁项集{0,1,2,3}可以生成的全部规则。如果某一条规则不满足最小置信度要求,那么该规则的所有子集也不会满足最小置信度的要求(如图中阴影部分所示)。我们可以利用这条性质来减少需要计算的规则数目,一旦发现某条规则不满足最小置信度的要求,那么这条规则的所有子集也就不用再去计算了。
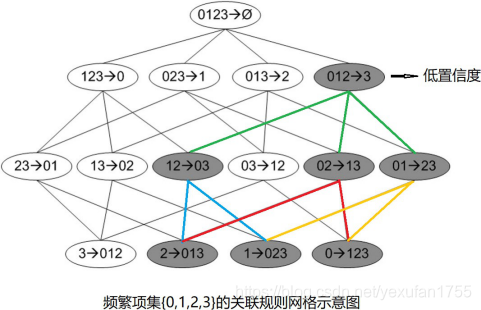
挖掘关联规则的流程为:首先从一个频繁项集开始,创建一个规则列表,其中规则右部只包含一个元素,然后计算这 些规则的置信度。接下来合并所有剩余规则,创建一个新的规则列表,其中右部包含两个元素,计算这些规则的置信 度……如此循环,遍历所有的规则。这种方法也被称为分级法 。
了解流程之后,我们尝试用python实现这一流程。
2. 关联规则的发掘python实现
我们直接在Apriori()函数挖掘出来的频繁项集的基础上来进一步挖掘满足置信度的关联规则,首先再来看一下Apriori()函数返回的结果:

其中,L是一个由频繁项集组成的list,**而supportData则包含了所有项集及其支持度。**对于L而言,第一个元素就是频繁一项集的list,第二个元素就是频繁二项集的list,以此类推。大家已经知道,置信度表示的是一个数据出现后另一个数据出现的概率(即条件概率),所以对于频繁一项集而言并无置信度的概念。频繁二项集的置信度相较于频繁 多项集(三项集及以上)更为简单,因此在计算置信度时,我们对频繁二项集和频繁多项集分别计算。
首先考虑频繁二项集,返回的L中包含了所有的频繁项集,直接取出频繁二项集L[1]
freqSet = L2[0] freqSet
#置信度的计算过程非常简单,借助集合运算以及Apriori的supportData计算结果,用频繁项集的支持度除以前驱项的支 持度即可,例如计算1→3的置信度:
supportData[freqSet]/supportData[freqSet-frozenset({3})]
#此处用到了集合减法运算求差集freqSet
freqSet - frozenset({3})
将其封装成函数:
"""
函数功能:根据单个频繁项集生成满足最小置信度的关联规则
参数说明:
freqSet:单个频繁项集
H:可以出现在关联规则右部的元素列表
supportData:所有项集及其支持度
brl:强关联规则列表
minConf:最小置信度
返回:
prunedH:关联规则右部元素列表
"""
def calcConf(freqSet, H, supportData, brl, minConf=0.5): prunedH = []
for conseq in H:
conf = supportData[freqSet]/supportData[freqSet-conseq]
if conf >= minConf:
print(freqSet-conseq,'-->',conseq,'conf:',conf)
brl.append((freqSet-conseq, conseq, conf))
prunedH.append(conseq)
return prunedH
测试函数:
brl=[]
H1 = [frozenset([item]) for item in freqSet]
calcConf(freqSet, H1, supportData, brl, minConf=0.5)

频繁多项集生成函数:
对于多项集,生成置信度规则的过程会更加复杂,在上述例子中,只有一个频繁三项集{2,3,5},接下来考虑计算该项集所能生成的规则置信度。首先仍然是将该频繁项集赋值给一个单独的变量,然后将其内部的每个元素单独保存为一个frozenset。
freqSet = L[2][0] freqSet
H2 = [frozenset([item]) for item in freqSet]
H2
#采用上述二项集置信度计算函数来计算前驱项只有一项的关联规则
calcConf(freqSet, H2, supportData, brl, minConf=0.5)
#然后用aprioriGen函数由一项集生成二项集
H3 = aprioriGen(H2)
H3
calcConf(freqSet, H3, supportData, brl, minConf=0.5)
将上述封装成函数:
"""
函数功能:根据单个频繁项集生成满足最小置信度的关联规则参数说明:
freqSet:单个频繁项集
H:频繁项集中的所有子项,可以放在规则右部的元素列表
brl:存放关联规则的容器
"""
def rulesFromConseq(freqSet, H, supportData, brl, minConf=0.7):
Hmp = True
while Hmp:
Hmp = False
H = calcConf(freqSet, H, supportData, brl, minConf)
H = aprioriGen(H)
Hmp = not(H == [] or len(H[0]) == len(freqSet))
测试函数:
freqSet = L[2][0]
H2 = [frozenset([item]) for item in freqSet]
brl = []
rulesFromConseq(freqSet, H2, supportData, brl, minConf=0.5)

生成关联规则的主函数:
"""
函数功能:生成所有满足最小置信度的关联规则
参数说明:
L:频繁项集
supportData:所有项集及其支持度
minConf:最小置信度
返回:
bigRuleList:满足最小置信度的关联规则(即强关联规则)
"""
def generateRules(L, supportData, minConf=0.7):
bigRuleList = [] #强关联规则容器
for i in range(1, len(L)): #对所有频繁项集循环操作,这里需要注意的是频繁1项集不存在关联规则
for freqSet in L[i]: # 对频繁项集中的每个子集关联规则进行挖掘
H1 = [frozenset([item]) for item in freqSet]
if (i > 1):
rulesFromConseq(freqSet, H1, supportData, bigRuleList,minConf) #频繁多项集
else:
calcConf(freqSet, H1, supportData, bigRuleList, minConf) #频繁二项集
return bigRuleList

五、案例:发现美国国会投票中的模式
| 特征索引 | 特征名称 |
|---|---|
| 0 | 党派(民主党,共和党) |
| 1 | 残疾人婴幼儿提案 |
| 2 | 水项目费用分摊 |
| 3 | 预算决议案 |
| 4 | 医生费用冻结决议案 |
| 5 | 萨尔瓦多援助 |
| 6 | 校园宗教团体决议 |
| 7 | 反卫星禁试决议 |
| 8 | 援助尼加拉瓜反政府 |
| 9 | MX导弹决议案 |
| 10 | 移民决议案 |
| 11 | 合成燃料公司削减决议 |
| 12 | 教育支出决议 |
| 13 | 超级基金起诉权 |
| 14 | 犯罪决议案 |
| 15 | 免税出口决议案 |
| 16 | 南非出口管理决议案 |
1.导入数据集并进行简单数据处理
文件在博客末尾。复制粘贴即可。
votes = pd.read_csv('house-votes-84.data.txt',sep=',',header=None) votes.head()
votes.shape #(435, 17)
#将列名修改为中文
votes.columns = ['党派','残疾人婴幼儿提案','水项目费用分摊','预算决议案'
,'医生费用冻结决议案','萨尔瓦多援助','校园宗教团体决议'
,'反卫星禁试决议','援助尼加拉瓜反政府','MX导弹决议案'
,'移民决议案','合成燃料公司削减决议','教育支出决议'
,'超级基金起诉权','犯罪决议案','免税出口决议案','南非出口管理决议案']
#将列名和投票结果合并
for i in range(1,votes.shape[1]):
votes.iloc[:,i] = votes.iloc[:,i].apply(lambda x:x+'-'+votes.columns[i])
#将数据变为列表
voteslist=votes.values.tolist()
2.挖掘所有的频繁项集
利用前面已经写好的Apriori算法来进行频繁项集的挖掘,这里设定默认的支持度阈值50%
L,suppData = apriori(voteslist, minSupport = 0.5)
'''
Out[56]:
[[frozenset({'残疾人婴幼儿提案-n'}),
frozenset({'校园宗教团体决议-y'}),
frozenset({'犯罪决议案-y'}),
frozenset({'免税出口决议案-n'}),
frozenset({'南非出口管理决议案-y'}),
frozenset({'合成燃料公司削减决议-n'}),
frozenset({'democrat'}),
frozenset({'预算决议案-y'}),
frozenset({'教育支出决议-n'}),
frozenset({'医生费用冻结决议案-n'}),
frozenset({'反卫星禁试决议-y'}),
frozenset({'援助尼加拉瓜反政府-y'})],
[frozenset({'democrat', '预算决议案-y'}),
frozenset({'democrat', '医生费用冻结决议案-n'}),
frozenset({'医生费用冻结决议案-n', '预算决议案-y'}),
frozenset({'democrat', '援助尼加拉瓜反政府-y'})],
[frozenset({'democrat', '医生费用冻结决议案-n', '预算决议案-y'})],
[]]
'''
3.挖掘强关联规则
这里设定置信度阈值为90%,利用generateRules函数可以挖掘出的关联规则有:
brl = generateRules(L, suppData, minConf=0.9)
挖掘出来的规则如下所示
frozenset({'预算决议案-y'}) --> frozenset({'democrat'}) conf 0.9130434782608695
frozenset({'医生费用冻结决议案-n'}) --> frozenset({'democrat'}) conf 0.9919028340080972
frozenset({'democrat'}) --> frozenset({'医生费用冻结决议案-n'}) conf 0.9176029962546816
frozenset({'援助尼加拉瓜反政府-y'}) --> frozenset({'democrat'}) conf 0.9008264462809917
frozenset({'预算决议案-y', '医生费用冻结决议案-n'}) --> frozenset({'democrat'}) conf 1.0
frozenset({'democrat', '预算决议案-y'}) --> frozenset({'医生费用冻结决议案-n'}) conf 0.9480519480519481
这些强规则是在支持度为50%的情况下挖掘出来的,也就是说,这些规则至少在50%以上的记录中出现过。对于{y-预算决议案,n-医生费用冻结决议案}→{democrat}这条规则,在100%的情况下是成立的,也就是说,这是一个必然事件,只要他给预算决议案投了赞成票,并且医生费用冻结决议案投了反对票,那么这个人一定是民主党。剩下的几条也都是很有意思的规则。
votes['党派'].value_counts() #统计各党派数量
votes['党派'].value_counts()/votes.shape[0] #计算各党派所占比例
从上述代码运行结果可以看出,**共和党所占比例仅为38.6%,如果设定支持度为50%,它根本就不会进入频繁项集。**如果我们一定想要查看共和党的一些特征,挖掘与共和党相关的一些强关联规则,那么我们可以将支持度降低一点, 比如30%,然后再来进行频繁项集的挖掘、关联规则的提取。但是需要提醒的是,如果降低了支持度,那频繁项集的 数量一定会很大程度的增加,那么置信度的设定就要更高一点,否则数据量大的话很容易卡死。
L,suppData = apriori(voteslist, minSupport = 0.3) #设定最小支持度为30%
brl = generateRules(L, suppData, minConf=0.99) #设定最小置信度为99%
#运行出来,会发现共有973个频繁项集,259条强关联规则
文件如下
house-votes-84.data.txt
republican,n,y,n,y,y,y,n,n,n,y,?,y,y,y,n,y
republican,n,y,n,y,y,y,n,n,n,n,n,y,y,y,n,?
democrat,?,y,y,?,y,y,n,n,n,n,y,n,y,y,n,n
democrat,n,y,y,n,?,y,n,n,n,n,y,n,y,n,n,y
democrat,y,y,y,n,y,y,n,n,n,n,y,?,y,y,y,y
democrat,n,y,y,n,y,y,n,n,n,n,n,n,y,y,y,y
democrat,n,y,n,y,y,y,n,n,n,n,n,n,?,y,y,y
republican,n,y,n,y,y,y,n,n,n,n,n,n,y,y,?,y
republican,n,y,n,y,y,y,n,n,n,n,n,y,y,y,n,y
democrat,y,y,y,n,n,n,y,y,y,n,n,n,n,n,?,?
republican,n,y,n,y,y,n,n,n,n,n,?,?,y,y,n,n
republican,n,y,n,y,y,y,n,n,n,n,y,?,y,y,?,?
democrat,n,y,y,n,n,n,y,y,y,n,n,n,y,n,?,?
democrat,y,y,y,n,n,y,y,y,?,y,y,?,n,n,y,?
republican,n,y,n,y,y,y,n,n,n,n,n,y,?,?,n,?
republican,n,y,n,y,y,y,n,n,n,y,n,y,y,?,n,?
democrat,y,n,y,n,n,y,n,y,?,y,y,y,?,n,n,y
democrat,y,?,y,n,n,n,y,y,y,n,n,n,y,n,y,y
republican,n,y,n,y,y,y,n,n,n,n,n,?,y,y,n,n
democrat,y,y,y,n,n,n,y,y,y,n,y,n,n,n,y,y
democrat,y,y,y,n,n,?,y,y,n,n,y,n,n,n,y,y
democrat,y,y,y,n,n,n,y,y,y,n,n,n,?,?,y,y
democrat,y,?,y,n,n,n,y,y,y,n,n,?,n,n,y,y
democrat,y,y,y,n,n,n,y,y,y,n,n,n,n,n,y,y
democrat,y,n,y,n,n,n,y,y,y,n,n,n,n,n,y,?
democrat,y,n,y,n,n,n,y,y,y,y,n,n,n,n,y,y
democrat,y,n,y,n,n,n,y,y,y,n,y,n,n,n,y,y
democrat,y,y,y,n,n,n,y,y,y,n,y,n,n,n,y,y
republican,y,n,n,y,y,n,y,y,y,n,n,y,y,y,n,y
democrat,y,y,y,n,n,n,y,y,y,n,y,n,n,n,y,y
republican,n,y,n,y,y,y,n,n,n,n,n,y,y,y,n,n
democrat,y,y,y,n,n,n,y,y,y,n,y,n,n,n,y,?
democrat,y,y,y,n,n,n,y,y,y,y,n,n,y,n,y,y
republican,n,y,n,y,y,y,n,n,n,n,n,y,y,y,n,y
democrat,y,y,y,n,n,n,y,y,y,n,n,n,n,n,y,y
republican,n,y,n,y,y,y,n,n,n,n,n,y,y,y,n,n
republican,y,?,n,y,y,y,n,n,n,y,n,y,?,y,n,y
republican,y,y,n,y,y,y,n,n,n,n,n,n,y,y,n,y
republican,n,y,n,y,y,y,n,n,n,y,n,y,y,y,n,n
democrat,y,n,y,n,n,n,y,y,y,y,y,n,y,n,y,y
democrat,y,y,y,n,n,n,y,y,y,n,?,n,n,n,n,?
democrat,y,y,y,n,n,n,y,y,y,n,n,n,n,n,y,?
democrat,y,n,y,n,n,n,y,y,y,n,n,n,n,n,n,y
democrat,y,n,y,n,n,n,y,y,y,n,n,n,n,n,y,y
democrat,y,y,y,n,n,n,y,y,y,n,y,n,n,n,n,?
democrat,y,y,y,n,n,n,y,y,?,n,y,n,n,n,y,?
democrat,y,y,y,n,n,n,y,y,y,n,n,n,n,n,n,y
democrat,y,n,y,n,n,n,y,y,?,n,n,n,n,n,n,?
democrat,y,y,y,n,n,n,y,y,n,n,n,n,n,y,n,y
republican,n,?,n,y,y,y,n,n,n,n,n,y,y,y,n,n
democrat,y,y,y,n,n,n,y,y,y,n,y,n,n,n,y,y
republican,n,y,n,y,y,y,n,?,n,n,n,y,y,y,n,y
democrat,y,y,y,n,n,n,y,y,y,n,n,n,n,n,?,?
republican,y,y,n,y,y,y,n,n,n,y,n,y,y,y,n,n
democrat,y,y,y,n,n,y,?,y,n,n,y,y,n,y,n,?
republican,n,y,n,y,y,y,n,n,n,y,y,y,y,y,n,n
republican,n,y,n,y,y,y,n,n,n,y,y,y,y,y,n,y
republican,n,y,n,y,y,y,n,n,n,y,n,y,y,y,n,y
republican,n,y,n,y,y,y,n,n,n,y,n,y,y,y,n,y
republican,n,y,n,y,y,y,n,n,n,y,n,y,y,y,n,?
democrat,y,y,y,n,n,?,y,y,y,y,n,n,n,n,y,?
republican,n,y,n,y,y,y,n,n,n,n,n,y,y,y,n,n
democrat,y,y,y,n,n,n,y,y,y,n,n,n,n,n,n,?
democrat,y,y,y,n,n,n,y,y,y,n,y,n,n,n,n,y
democrat,y,y,y,n,n,n,y,y,y,n,y,?,n,n,n,y
republican,y,y,n,y,y,y,y,n,n,n,n,y,y,y,n,y
republican,n,y,n,y,y,y,y,n,n,n,y,y,y,y,n,y
republican,n,y,n,y,y,y,n,n,n,y,n,y,y,y,n,n
democrat,y,?,y,n,n,n,y,y,y,n,n,n,y,n,y,y
democrat,y,y,y,n,n,n,y,y,y,n,n,n,n,n,y,y
democrat,y,n,y,n,n,n,y,y,y,n,n,n,y,n,y,?
republican,y,y,y,y,n,n,y,y,y,y,y,n,n,y,n,y
democrat,y,y,y,n,n,n,y,y,y,n,y,n,n,n,y,?
republican,y,n,y,y,y,n,y,n,y,y,n,n,y,y,n,y
democrat,y,n,y,n,n,y,y,y,y,y,y,n,n,y,y,y
democrat,n,y,y,y,y,y,n,n,n,y,y,n,y,y,n,n
democrat,n,y,y,n,y,y,n,n,n,y,y,y,y,y,n,?
democrat,n,y,y,y,y,y,n,y,y,y,y,y,y,y,n,y
democrat,y,y,y,n,y,y,n,n,n,y,y,n,y,y,n,y
republican,n,n,n,y,y,n,n,n,n,y,n,y,y,y,n,n
democrat,y,n,y,n,n,y,y,y,y,y,n,y,n,y,n,?
democrat,y,n,y,n,n,n,y,y,?,y,y,y,n,y,n,y
republican,n,n,n,y,y,y,n,n,n,y,n,y,y,y,n,y
republican,n,n,n,y,y,y,n,n,n,n,n,y,y,y,n,n
republican,n,?,n,y,y,y,n,n,n,y,n,y,y,y,n,n
democrat,n,n,y,n,y,y,n,n,n,y,y,y,y,y,n,y
republican,n,n,n,y,y,y,n,n,n,y,n,y,y,y,n,n
republican,n,n,n,y,y,y,n,n,n,n,n,y,y,y,n,n
democrat,n,y,y,n,y,y,y,n,y,y,y,n,y,y,n,y
republican,n,n,n,y,y,y,n,n,n,y,n,?,y,y,n,?
democrat,y,n,y,n,n,n,y,y,y,y,n,n,n,n,y,y
democrat,y,n,y,n,n,n,y,y,y,y,y,n,n,n,y,y
democrat,y,y,y,n,n,n,y,y,n,y,y,n,n,?,y,y
democrat,y,n,y,n,n,n,y,n,y,y,y,n,n,n,y,y
democrat,y,n,y,n,y,y,n,n,n,n,n,n,n,n,n,y
democrat,y,n,y,n,y,y,n,?,?,n,y,?,?,?,y,y
democrat,n,n,?,n,y,y,n,n,n,n,y,y,y,y,n,y
democrat,y,n,n,n,y,y,y,n,n,y,y,n,n,y,n,y
democrat,y,y,y,n,n,y,y,y,y,y,n,n,n,n,n,y
republican,n,n,n,y,y,y,n,n,n,y,?,y,y,y,n,n
democrat,y,n,n,n,y,y,n,n,n,n,y,y,n,y,n,y
democrat,y,n,y,n,y,y,y,n,n,n,y,n,n,y,n,y
democrat,y,n,y,n,y,y,y,n,?,n,y,n,y,y,y,?
democrat,y,n,n,n,y,y,?,n,?,n,n,n,n,y,?,n
democrat,?,?,?,?,n,y,y,y,y,y,?,n,y,y,n,?
democrat,y,y,y,n,n,n,n,y,y,n,y,n,n,n,y,y
republican,n,y,n,y,y,y,n,n,n,n,n,y,y,y,n,y
republican,n,?,?,?,?,?,?,?,?,?,?,?,?,y,?,?
democrat,y,?,y,n,n,n,y,y,y,n,n,n,n,n,y,?
democrat,y,?,y,n,n,n,y,y,y,n,n,n,n,n,y,?
democrat,n,n,y,n,n,n,y,y,y,y,n,n,n,n,y,y
republican,n,?,n,y,y,y,n,n,n,y,n,y,y,y,n,y
democrat,n,?,y,n,n,y,y,y,n,y,n,n,n,n,y,?
republican,n,?,n,y,y,y,n,n,n,y,n,y,y,y,n,n
democrat,y,?,y,n,n,n,y,y,y,n,n,n,n,n,y,?
democrat,n,?,y,n,?,?,y,y,y,y,?,?,n,n,y,y
democrat,y,n,y,n,n,n,y,y,y,n,y,n,n,n,y,y
republican,y,y,y,y,y,n,y,n,n,n,n,y,y,y,n,y
democrat,n,y,y,n,n,n,n,y,y,y,y,n,n,n,y,y
republican,n,n,n,y,y,y,n,n,n,n,n,y,y,y,n,n
republican,n,?,?,y,y,y,n,n,n,y,n,y,y,y,?,y
republican,n,?,n,y,y,y,n,n,n,y,n,y,y,y,n,y
republican,n,n,n,y,y,y,n,n,n,y,n,y,n,y,n,y
republican,y,?,n,y,y,y,n,y,n,n,n,y,y,y,n,y
democrat,n,?,y,n,n,n,y,y,y,n,n,n,n,n,y,y
republican,n,?,n,y,y,y,n,n,n,y,n,y,y,y,n,y
republican,n,?,n,y,y,y,n,n,n,n,n,y,y,y,n,n
democrat,n,?,y,n,n,n,y,y,y,y,y,n,n,y,y,y
democrat,n,?,y,n,n,y,n,y,n,y,y,n,n,n,y,y
democrat,?,?,y,n,n,n,y,y,?,n,?,?,?,?,?,?
democrat,y,?,y,n,?,?,y,y,y,n,n,n,n,n,y,?
democrat,n,n,y,n,n,y,n,y,y,y,n,n,n,y,n,y
republican,n,n,n,y,y,y,n,n,n,y,n,y,y,y,n,?
republican,n,n,n,y,y,y,n,n,n,y,n,y,y,y,n,y
republican,n,n,n,y,y,y,n,n,n,n,n,y,y,y,n,?
republican,n,n,n,y,y,y,n,n,n,y,n,y,y,y,n,n
republican,n,y,n,y,y,y,n,n,n,y,y,y,y,n,n,y
democrat,n,?,y,n,n,y,y,y,y,y,n,n,n,y,y,y
democrat,n,n,y,n,n,y,y,y,y,y,n,n,n,y,n,y
democrat,y,n,y,n,n,y,y,y,y,n,n,n,n,n,y,y
republican,n,n,n,y,n,n,y,y,y,y,n,n,y,y,n,y
republican,n,n,n,y,y,y,y,y,y,y,n,y,y,y,?,y
republican,n,n,n,y,y,y,y,y,y,y,n,y,y,y,n,y
democrat,?,y,n,n,n,n,y,y,y,y,y,n,n,y,y,y
democrat,n,?,n,n,n,y,y,y,y,y,n,n,n,y,n,?
democrat,n,n,y,n,n,y,y,y,y,y,n,n,n,y,?,y
republican,n,y,n,y,y,y,n,n,n,n,n,y,y,y,n,y
democrat,n,n,n,n,n,n,y,y,y,y,n,y,y,y,y,y
republican,n,y,n,y,y,y,n,n,n,y,y,y,y,y,n,y
democrat,n,n,y,n,n,n,y,y,y,y,n,n,y,n,y,y
republican,y,y,n,y,y,y,n,n,n,y,n,y,y,y,n,y
democrat,y,y,?,y,y,y,n,n,y,n,y,?,y,y,n,n
democrat,n,y,y,n,n,y,n,y,y,y,y,n,y,n,y,y
democrat,n,n,y,n,n,y,y,y,y,y,y,n,y,y,n,y
republican,n,y,n,y,y,y,n,n,n,n,n,y,y,y,n,n
republican,y,y,n,y,y,y,n,?,n,n,y,y,y,y,n,n
republican,y,y,n,y,y,y,y,n,n,n,n,y,y,y,n,n
democrat,n,y,y,n,n,y,n,y,y,n,y,n,?,?,?,?
republican,n,y,n,y,y,y,n,n,n,y,n,y,y,y,n,n
democrat,n,y,y,n,?,y,y,y,y,y,y,n,n,?,n,?
democrat,n,y,n,n,y,y,n,n,n,n,n,y,y,y,y,y
democrat,n,n,n,n,y,y,y,n,n,n,n,y,y,y,n,y
democrat,n,y,y,n,y,y,y,n,n,n,y,y,y,y,n,y
republican,n,y,n,y,y,y,y,n,n,n,n,y,y,y,n,y
democrat,y,y,n,n,y,y,n,n,n,y,y,y,y,y,n,?
democrat,n,y,y,n,n,y,y,y,y,y,y,n,y,n,y,?
republican,y,n,y,y,y,y,y,y,n,y,n,y,n,y,y,y
republican,y,n,y,y,y,y,y,y,n,y,y,y,n,y,y,y
democrat,n,n,y,y,y,y,n,n,y,n,n,n,y,y,y,?
democrat,y,n,y,n,n,n,y,y,y,y,y,n,n,y,n,y
democrat,y,n,y,n,n,n,?,y,y,?,n,n,n,n,y,?
republican,n,?,n,y,y,y,n,n,n,y,n,y,y,y,n,y
democrat,n,y,y,n,n,n,y,y,y,y,n,n,?,n,y,y
democrat,n,n,n,n,y,y,n,n,n,y,y,y,y,y,n,y
democrat,y,?,y,n,n,n,y,y,y,n,n,n,n,n,y,?
democrat,n,y,y,n,n,n,y,y,y,y,n,n,n,n,y,y
republican,n,n,y,y,n,n,y,y,y,y,n,n,n,y,y,y
democrat,n,n,y,n,n,n,y,y,y,y,y,?,n,n,y,y
democrat,?,n,y,n,n,n,y,y,y,y,y,?,n,n,y,?
democrat,y,n,y,n,n,n,y,y,y,y,n,n,n,n,y,y
democrat,?,?,y,n,n,n,y,y,y,?,?,n,n,n,?,?
democrat,n,n,y,n,n,n,y,y,y,y,y,n,n,n,y,y
democrat,y,?,y,n,n,n,y,y,y,n,n,n,n,n,y,y
democrat,?,?,?,?,?,?,?,?,y,?,?,?,?,?,?,?
democrat,n,n,y,n,n,n,y,y,y,y,y,n,n,n,y,y
democrat,y,n,y,n,n,n,y,y,y,y,n,?,n,n,y,y
democrat,n,y,y,n,n,n,y,y,y,y,y,n,n,n,y,y
democrat,y,n,y,n,n,n,y,y,y,n,n,n,n,n,y,?
republican,y,?,n,y,y,y,y,y,n,n,n,y,?,y,?,?
democrat,y,n,y,n,n,n,y,y,y,n,n,n,n,n,y,y
republican,n,?,n,y,y,y,n,n,n,n,n,y,y,y,n,?
republican,n,y,n,y,y,y,n,?,n,y,n,y,y,y,n,?
democrat,n,n,n,n,n,y,y,y,y,n,y,n,n,y,y,y
democrat,n,n,y,n,n,n,y,y,y,n,n,n,n,n,y,y
democrat,n,n,y,n,n,y,y,?,y,y,y,n,n,n,y,y
republican,n,n,n,y,y,y,n,n,n,n,n,y,y,y,n,?
democrat,n,n,y,n,n,y,y,y,y,n,y,y,n,y,y,?
republican,n,?,y,y,y,y,n,n,n,y,n,n,n,y,n,y
democrat,n,n,y,n,n,n,y,y,y,y,y,n,?,n,y,?
democrat,y,y,n,n,n,n,y,y,?,n,y,n,n,n,y,?
democrat,n,n,y,n,n,n,y,y,y,n,n,n,n,y,y,y
democrat,y,y,y,n,n,n,y,y,y,n,n,n,n,n,y,y
democrat,y,n,y,n,n,y,y,y,y,y,y,n,n,n,y,y
democrat,y,n,y,n,n,n,y,y,y,y,n,n,n,n,y,y
republican,n,n,y,y,y,y,y,n,n,n,n,y,y,y,n,y
democrat,n,n,y,n,n,y,y,y,y,y,n,y,n,n,n,y
republican,n,n,n,y,y,y,n,n,n,y,n,y,n,y,n,y
republican,y,?,n,y,y,y,y,n,n,y,n,y,y,y,n,y
democrat,n,n,y,n,n,n,y,y,y,n,n,?,n,n,y,y
democrat,y,y,y,n,n,n,y,y,y,y,y,n,n,n,n,y
democrat,n,n,y,n,n,y,y,y,y,n,n,n,n,n,y,y
republican,n,y,n,y,y,y,n,n,n,y,n,y,y,y,n,y
democrat,n,n,y,n,n,n,y,y,y,n,y,n,n,n,y,y
democrat,n,y,y,n,n,y,n,y,y,n,y,n,y,n,y,y
republican,y,y,n,y,y,y,n,n,n,y,n,y,y,y,n,y
democrat,n,y,y,y,y,y,n,n,n,y,y,y,y,y,y,?
democrat,y,y,y,n,y,y,n,n,?,y,n,n,n,y,y,?
republican,n,y,n,y,y,y,n,n,n,y,n,y,y,y,n,n
democrat,y,?,y,n,n,n,y,y,y,n,?,n,n,n,y,?
democrat,n,y,y,n,n,n,n,y,y,n,y,n,n,y,y,y
democrat,n,n,y,n,n,n,y,y,y,n,n,n,n,n,y,?
democrat,n,y,y,n,y,y,n,n,n,n,y,n,n,n,y,?
democrat,y,n,y,n,n,n,y,y,y,n,y,n,n,n,y,?
republican,n,n,n,y,y,n,n,n,n,n,n,y,y,y,n,y
republican,n,y,n,y,y,y,n,n,n,y,n,?,y,y,n,n
republican,n,?,n,y,y,y,n,n,n,n,n,y,y,y,n,y
democrat,n,n,y,n,n,y,y,y,y,n,y,n,n,y,y,y
democrat,y,n,y,n,n,n,y,y,y,n,n,n,n,n,?,y
republican,n,y,n,y,y,y,n,n,n,n,n,y,y,?,n,y
republican,n,y,y,y,y,y,y,n,y,y,n,y,y,y,n,y
republican,n,y,n,y,y,y,n,n,n,n,n,y,y,y,n,y
republican,n,y,n,y,y,y,n,n,y,y,n,y,y,y,n,y
democrat,n,y,y,n,n,n,y,y,n,n,y,n,n,n,y,?
republican,n,y,n,y,y,y,n,n,n,y,n,y,y,y,n,y
democrat,n,n,y,n,n,y,y,y,y,y,n,y,n,y,y,?
republican,n,n,n,y,y,y,n,n,n,y,n,y,n,y,n,y
democrat,n,n,y,n,n,n,y,y,y,n,n,n,n,n,y,y
democrat,y,n,y,n,n,y,y,y,n,n,n,y,y,n,n,y
democrat,y,y,y,n,n,n,y,y,?,y,n,n,n,n,y,?
republican,n,n,n,y,y,y,y,n,n,y,n,n,n,y,y,y
republican,n,n,n,y,n,y,y,?,y,n,n,y,y,y,n,y
democrat,y,n,y,n,n,n,y,y,y,y,y,n,n,y,y,y
republican,n,n,n,n,y,y,y,n,n,n,n,?,n,y,y,y
democrat,n,y,y,n,n,n,y,y,?,y,n,n,y,n,y,y
democrat,y,n,y,n,n,n,n,y,y,y,n,n,n,n,y,y
democrat,y,n,y,n,n,n,y,y,y,y,y,n,n,n,y,y
democrat,n,n,y,n,y,n,y,y,y,n,n,n,n,y,?,y
republican,n,y,n,y,y,y,?,n,n,n,n,?,y,y,n,n
republican,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?
democrat,y,n,y,n,n,n,y,y,?,n,y,n,n,n,y,y
republican,n,y,n,y,y,y,n,n,n,n,n,y,y,y,n,n
republican,n,y,n,y,y,y,n,n,n,n,n,y,y,y,n,n
democrat,y,y,y,n,n,y,y,y,y,n,n,n,n,n,y,y
republican,n,y,n,y,y,y,n,n,n,n,n,y,y,y,n,y
democrat,y,n,y,n,n,n,y,y,y,y,n,n,n,n,n,y
democrat,y,n,y,n,n,n,y,y,y,y,n,n,n,y,y,y
republican,n,n,n,y,y,n,n,n,n,n,n,y,n,y,n,n
republican,n,n,n,y,y,n,n,n,n,n,n,y,n,y,?,y
democrat,n,n,y,n,n,n,y,y,y,n,y,n,n,n,y,y
democrat,y,n,y,n,n,n,y,y,y,n,n,n,n,n,n,y
democrat,y,n,y,n,n,n,y,y,y,y,n,n,n,n,n,y
democrat,y,n,y,n,n,?,y,y,y,n,?,?,n,?,?,?
democrat,y,n,y,n,n,n,y,y,y,y,n,n,?,n,y,y
democrat,y,n,y,n,n,n,y,y,y,n,n,n,n,n,y,?
democrat,y,n,y,n,n,n,y,y,y,n,n,n,n,n,y,?
democrat,y,n,y,n,n,n,y,y,y,y,n,n,n,n,n,y
republican,n,n,n,y,y,y,n,n,n,y,n,y,n,y,n,y
republican,y,n,n,n,n,n,y,y,y,y,n,n,n,y,n,y
democrat,y,n,y,n,n,n,y,y,y,n,n,n,n,n,y,?
democrat,y,n,y,n,n,n,y,y,y,n,n,n,n,n,n,y
democrat,y,y,y,n,n,n,y,y,y,n,n,n,n,n,y,y
democrat,n,y,y,n,n,y,y,y,y,n,?,n,n,n,n,y
democrat,y,n,y,n,n,n,y,y,y,y,n,n,n,n,y,?
republican,n,n,n,y,y,n,y,y,n,y,n,y,y,y,?,y
republican,y,n,n,y,y,n,y,n,n,y,n,n,n,y,y,y
democrat,n,n,y,n,y,y,n,n,n,n,?,n,y,y,n,n
republican,n,n,n,y,y,y,n,n,n,n,n,y,y,y,y,n
republican,n,n,y,y,y,y,y,y,n,y,n,n,n,y,n,y
republican,n,n,n,y,y,y,n,n,n,n,n,y,y,y,n,y
republican,n,n,n,y,y,y,n,n,n,y,n,y,y,y,n,n
democrat,n,n,y,n,n,n,y,y,y,y,n,n,n,y,n,y
republican,y,n,y,y,y,y,y,y,n,n,n,n,n,y,n,?
republican,y,n,n,y,y,y,n,n,n,y,n,?,y,y,n,n
republican,n,n,n,y,y,y,n,n,n,n,n,y,y,y,n,y
democrat,n,n,y,n,n,y,y,y,y,y,y,n,n,n,?,y
democrat,n,n,y,n,n,y,y,y,y,y,y,n,n,n,y,y
democrat,n,n,y,n,n,y,?,y,?,y,y,y,n,y,y,?
democrat,y,y,y,?,n,y,y,y,y,n,y,n,y,n,?,y
democrat,y,y,y,n,y,y,n,y,n,y,y,n,y,y,y,y
democrat,y,y,y,n,y,y,n,y,n,y,y,n,y,y,n,?
democrat,y,n,y,n,?,y,?,y,y,y,n,n,y,y,n,y
democrat,y,n,y,n,n,y,y,y,y,y,n,?,n,y,n,y
democrat,y,n,y,n,n,y,y,y,n,y,y,n,y,y,y,y
democrat,y,y,y,n,n,y,y,y,y,y,y,n,y,y,y,y
democrat,n,y,y,n,n,y,y,y,n,y,y,n,y,y,n,?
republican,n,y,n,y,y,y,?,?,n,y,n,y,?,?,?,?
republican,n,n,y,y,y,y,n,n,n,y,n,y,y,y,y,y
democrat,y,y,y,n,n,y,y,y,y,y,n,n,?,n,y,?
democrat,n,y,n,n,n,n,y,y,y,y,y,n,n,n,y,y
democrat,n,y,y,n,n,y,y,y,y,y,n,n,y,y,y,y
republican,n,n,n,y,y,n,y,y,y,y,n,y,y,y,n,y
democrat,n,n,?,n,n,y,y,y,y,n,n,n,n,n,y,y
republican,n,n,n,y,y,y,y,n,n,y,n,y,y,y,n,y
republican,n,n,n,y,y,y,n,n,n,n,n,y,y,y,n,n
republican,n,y,n,y,y,y,n,n,n,y,n,y,y,y,n,?
republican,n,n,n,y,y,y,n,n,n,y,n,y,y,y,n,n
republican,n,n,n,y,y,y,n,n,n,n,n,y,y,y,n,n
democrat,y,n,y,n,n,y,y,y,y,n,n,n,n,y,n,?
republican,n,n,n,y,y,y,n,n,n,y,n,y,y,y,n,n
democrat,y,n,n,n,n,y,y,y,y,y,n,n,n,y,y,y
republican,n,n,n,y,y,y,n,n,n,y,n,y,y,y,y,n
democrat,n,n,y,n,n,y,y,y,y,y,n,n,y,n,n,y
democrat,y,y,y,n,n,n,y,y,y,y,n,n,n,n,y,y
republican,n,y,y,y,y,y,n,n,n,y,n,y,y,y,n,y
republican,n,y,n,y,y,y,y,y,n,n,y,y,y,y,y,y
republican,n,y,y,y,y,y,y,?,n,n,n,n,?,?,y,?
democrat,n,n,n,n,n,y,n,y,y,n,y,y,y,y,y,n
democrat,y,n,n,n,n,n,y,y,y,y,n,n,n,n,y,y
democrat,n,n,y,n,n,n,y,y,y,n,n,n,n,n,y,?
democrat,y,n,y,n,n,n,y,y,y,n,n,n,n,n,y,?
democrat,n,y,y,n,n,y,n,y,y,y,n,n,y,y,n,y
democrat,y,y,y,n,n,n,y,y,y,y,n,n,y,n,n,y
democrat,y,y,y,n,?,y,n,?,n,n,y,n,y,y,n,?
democrat,y,y,y,n,y,y,n,y,?,y,n,n,y,y,n,?
republican,n,y,n,y,y,y,n,n,n,n,y,y,y,y,n,n
democrat,n,y,n,n,y,y,n,n,?,n,n,y,y,y,n,y
democrat,y,y,n,y,n,n,y,y,y,n,y,n,n,y,n,y
republican,n,y,n,y,y,y,n,n,n,n,n,y,y,y,n,y
democrat,y,y,y,n,n,n,y,y,y,n,y,n,n,n,n,y
democrat,y,?,y,n,n,y,y,y,y,y,n,n,n,n,y,?
republican,n,y,n,y,y,y,n,n,n,y,n,y,y,y,n,n
democrat,y,?,y,n,n,n,y,y,y,n,n,n,n,n,y,?
democrat,y,n,y,n,n,n,y,y,y,n,y,n,n,n,y,?
democrat,n,n,y,n,n,n,y,y,y,n,n,n,n,n,y,y
democrat,n,y,y,n,n,y,y,y,?,n,y,y,n,n,y,y
republican,n,n,n,y,y,y,n,n,n,y,y,y,y,y,n,?
democrat,n,n,y,n,n,y,y,y,n,n,y,n,n,y,?,y
democrat,y,n,y,n,n,n,y,y,y,n,n,n,n,n,y,y
democrat,y,n,y,n,n,n,y,y,y,y,n,n,n,y,y,y
republican,y,n,n,y,y,y,n,n,n,n,y,y,y,y,n,n
republican,n,n,n,y,y,y,n,n,n,y,y,y,n,y,n,y
democrat,n,?,y,?,n,y,y,y,y,y,y,n,?,?,y,y
democrat,n,y,y,n,y,?,y,n,n,y,y,n,y,n,y,y
republican,n,n,n,y,y,n,y,n,y,y,n,n,n,y,n,y
democrat,n,n,y,n,n,n,y,y,y,y,y,n,n,n,y,y
republican,n,n,n,y,y,y,y,n,n,y,n,y,n,y,y,y
republican,n,n,n,y,y,y,n,n,n,y,n,y,y,y,n,y
republican,y,n,n,y,y,y,n,n,n,y,n,y,y,y,n,n
democrat,y,n,y,n,n,n,y,y,y,y,n,y,n,n,y,?
republican,n,y,y,y,y,y,y,y,y,n,n,y,y,y,n,y
democrat,n,y,n,n,n,y,y,n,y,n,y,n,n,n,y,y
republican,n,n,y,y,y,y,y,y,y,y,n,y,y,y,y,y
democrat,n,y,n,y,n,y,y,y,y,n,y,n,y,n,y,?
republican,n,n,y,y,y,y,y,n,n,y,y,y,y,y,n,y
democrat,n,y,y,n,n,y,y,y,y,y,n,?,n,n,y,y
republican,y,n,y,y,n,n,n,y,y,y,n,n,n,y,y,y
republican,n,n,n,y,y,y,n,n,n,n,n,y,y,y,n,n
republican,n,n,n,y,y,y,n,n,n,n,n,y,y,y,n,n
democrat,y,y,y,n,n,y,y,y,y,y,y,y,y,y,n,?
republican,n,n,n,y,y,y,n,n,n,y,?,y,y,y,n,y
democrat,y,n,y,n,n,y,y,y,y,y,n,n,y,n,n,y
democrat,y,n,y,n,y,y,y,n,y,y,n,n,y,y,n,?
democrat,y,y,y,n,n,y,y,y,y,y,y,y,y,n,n,y
republican,y,y,n,y,y,y,n,n,n,y,y,n,y,n,n,n
republican,y,y,n,y,y,y,n,n,n,n,y,n,y,y,n,y
democrat,n,y,n,n,y,y,n,n,n,y,y,n,y,y,n,n
democrat,y,n,y,n,n,n,y,y,n,y,y,n,n,n,n,?
democrat,y,y,y,n,y,y,y,y,n,y,y,n,n,n,y,?
democrat,n,y,y,n,n,y,y,y,n,y,n,n,n,n,y,y
republican,n,y,n,y,y,y,n,n,n,n,n,n,y,y,n,y
democrat,y,y,y,n,?,y,y,y,n,y,?,?,n,n,y,y
democrat,y,y,y,n,?,n,y,y,y,y,n,n,n,n,y,?
democrat,n,y,y,y,y,y,n,n,n,n,y,y,?,y,n,n
democrat,n,y,y,?,y,y,n,y,n,y,?,n,y,y,?,y
republican,n,y,n,y,y,y,n,n,n,n,n,y,y,y,n,y
democrat,n,y,n,y,y,y,n,n,n,n,y,y,n,y,n,n
democrat,y,?,y,n,n,n,y,y,y,n,y,n,n,n,y,y
republican,n,y,n,y,y,y,?,?,n,n,?,?,y,?,?,?
republican,n,n,n,y,y,y,n,n,n,n,n,y,y,y,n,y
republican,n,n,n,y,y,y,n,n,n,n,n,y,y,y,n,y
democrat,y,y,y,n,n,y,?,y,y,n,y,n,y,n,y,y
democrat,y,y,y,n,y,y,y,y,y,y,y,n,y,y,n,?
democrat,y,y,n,y,y,y,n,n,n,n,y,n,y,y,n,?
democrat,y,y,y,n,y,y,n,y,y,y,y,n,n,n,n,y
democrat,y,y,y,y,y,y,n,n,n,n,y,y,y,y,n,y
democrat,y,y,n,n,y,y,n,n,n,n,y,y,y,y,y,n
democrat,n,?,y,n,y,y,n,y,n,n,y,n,n,n,n,?
democrat,y,y,y,n,y,y,n,y,y,n,y,n,n,y,n,?
democrat,n,y,y,y,y,y,n,n,n,n,n,y,y,y,n,?
democrat,y,n,y,n,n,n,y,y,y,?,y,n,n,n,y,?
democrat,?,?,n,n,?,y,?,n,n,n,y,y,n,y,n,?
democrat,y,y,n,n,n,n,n,y,y,n,y,n,n,n,y,n
republican,y,y,n,y,y,y,n,n,n,n,y,y,y,y,n,y
republican,?,?,?,?,n,y,n,y,y,n,n,y,y,n,n,?
democrat,y,y,?,?,?,y,n,n,n,n,y,n,y,n,n,y
democrat,y,y,y,?,n,n,n,y,n,n,y,?,n,n,y,y
democrat,y,y,y,n,y,y,n,y,n,n,y,n,y,n,y,y
democrat,y,y,n,n,y,?,n,n,n,n,y,n,y,y,n,y
democrat,n,y,y,n,y,y,n,y,n,n,n,n,n,n,n,y
republican,n,y,n,y,?,y,n,n,n,y,n,y,y,y,n,n
republican,n,y,n,y,y,y,n,?,n,n,?,?,?,y,n,?
republican,n,y,n,y,y,y,n,n,n,y,y,y,y,y,n,n
republican,?,n,y,y,n,y,y,y,y,y,n,y,n,y,n,y
republican,n,y,n,y,y,y,n,n,n,y,n,y,?,y,n,n
republican,y,y,n,y,y,y,n,n,n,y,n,y,y,y,n,y
republican,n,n,n,y,y,y,n,n,n,n,n,y,y,y,n,y
democrat,y,n,y,n,y,y,n,n,y,y,n,n,y,y,n,y
democrat,n,n,n,y,y,y,n,n,n,n,y,y,y,y,n,n
democrat,y,n,y,n,n,y,y,y,y,n,n,y,?,y,y,y
republican,n,n,n,y,y,y,n,n,n,n,n,y,y,y,n,n
republican,n,n,n,y,y,y,n,n,n,n,y,y,y,y,n,y
democrat,y,n,y,n,n,y,y,y,y,y,y,n,n,n,n,y
republican,n,n,n,y,y,y,n,n,n,y,n,y,y,y,n,y
republican,y,y,y,y,y,y,y,y,n,y,?,?,?,y,n,y
democrat,y,y,y,n,n,n,y,y,y,n,n,n,n,n,n,y
democrat,n,y,y,n,n,y,y,y,?,y,n,n,n,n,n,y
republican,y,y,n,y,y,y,n,n,n,y,n,n,y,y,n,y
democrat,y,y,y,n,n,n,y,y,y,y,y,n,y,n,n,y
democrat,y,y,y,n,n,n,y,y,n,y,n,n,n,n,n,y
democrat,y,y,y,n,n,n,y,y,y,n,n,n,n,n,n,y
republican,y,y,y,y,y,y,y,y,n,y,n,n,y,y,n,y
democrat,n,y,y,n,y,y,y,y,n,n,y,n,y,n,y,y
democrat,n,n,y,n,n,y,y,y,y,n,y,n,n,n,y,y
democrat,n,y,y,n,n,y,y,y,y,n,y,n,n,y,y,y
democrat,n,y,y,n,n,?,y,y,y,y,y,n,?,y,y,y
democrat,n,n,y,n,n,n,y,y,n,y,y,n,n,n,y,?
democrat,y,n,y,n,n,n,y,y,y,y,n,n,n,n,y,y
republican,n,n,n,y,y,y,y,y,n,y,n,y,y,y,n,y
democrat,?,?,?,n,n,n,y,y,y,y,n,n,y,n,y,y
democrat,y,n,y,n,?,n,y,y,y,y,n,y,n,?,y,y
republican,n,n,y,y,y,y,n,n,y,y,n,y,y,y,n,y
democrat,n,n,y,n,n,n,y,y,y,y,n,n,n,n,n,y
republican,n,?,n,y,y,y,n,n,n,n,y,y,y,y,n,y
republican,n,n,n,y,y,y,?,?,?,?,n,y,y,y,n,y
republican,n,y,n,y,y,y,n,n,n,y,n,y,y,y,?,n

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








