[LeetCode] 232. 用栈实现队列

最新推荐文章于 2025-02-18 23:34:04 发布

原创最新推荐文章于 2025-02-18 23:34:04 发布 · 122 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#队列 #栈

本文详细介绍了如何使用Python和C++实现一个队列，通过利用两个栈（一个用于输入，一个用于输出）来保持先进先出的特性。讲解了基本原理、代码实现及空栈处理策略。

[LeetCode] 232. 用栈实现队列

解题思路

两个数据结构的概念：

栈：后进先出
队列：先进先出

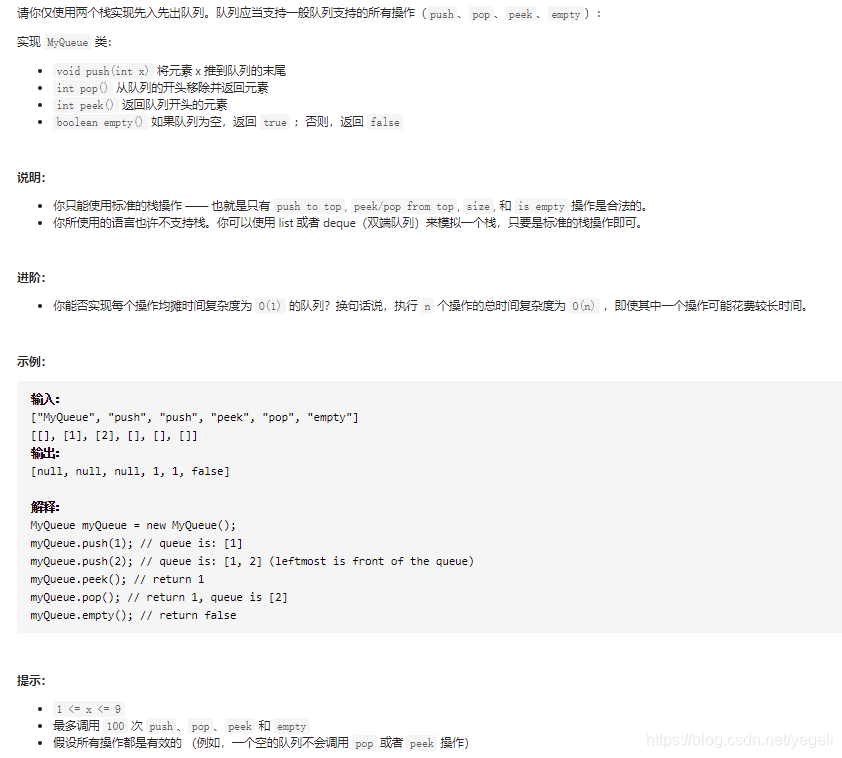
题目让我们用两个栈来实现一个队列，就是要让两个栈实现一个先进先出的数据结构。
思路是：「输入栈」会把输入顺序颠倒；如果把「输入栈」的元素逐个弹出放到「输出栈」，再从「输出栈」弹出元素的时候，则可以负负得正，实现了先进先出。

具体做法：

可以把一个栈当做「输入栈」，把另一个栈当做「输出栈」。
当 push() 新元素的时候，放到「输入栈」的栈顶，记此顺序为「输入序」。
当 pop() 元素的时候，是从「输出栈」弹出元素。如果「输出栈」为空，则把「输入栈」的元素逐个 pop() 并且 push() 到「输出栈」中，这一步会把「输入栈」的栈底元素放到了「输出栈」的栈顶。此时负负得正，从「输出栈」的 pop() 元素的顺序与「输入序」相同。

python解法：

class MyQueue:
    def __init__(self):
        self.a = []
        self.b = []

    def push(self, x: int) -> None:
        while self.b:
            self.a.append(self.b.pop())
        self.a.append(x)
        while self.a:
            self.b.append(self.a.pop())

    def pop(self) -> int:
        return self.b.pop()

    def peek(self) -> int:
        return self.b[-1] 


    def empty(self) -> bool:
        return len(self.b) == 0

C++解法

class MyQueue {
private:
    stack<int> inStack, outStack;

    void in2out() {
        while (!inStack.empty()) {
            outStack.push(inStack.top());
            inStack.pop();
        }
    }

public:
    MyQueue() {}

    void push(int x) {
        inStack.push(x);
    }

    int pop() {
        if (outStack.empty()) {
            in2out();
        }
        int x = outStack.top();
        outStack.pop();
        return x;
    }

    int peek() {
        if (outStack.empty()) {
            in2out();
        }
        return outStack.top();
    }

    bool empty() {
        return inStack.empty() && outStack.empty();
    }
};