# -*- coding: utf-8 -*-
###############################################################################
####################### 正文代码 #######################
###############################################################################
# 代码 3-5
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = 'SimHei' ## 设置中文显示
plt.rcParams['axes.unicode_minus'] = False
data = np.load('../data/国民经济核算季度数据.npz')
name = data['columns'] ## 提取其中的columns数组,视为数据的标签
values = data['values']## 提取其中的values数组,数据的存在位置
plt.figure(figsize=(8,7))## 设置画布
plt.scatter(values[:,0],values[:,2], marker='o')## 绘制散点图
plt.xlabel('年份')## 添加横轴标签
plt.ylabel('生产总值(亿元)')## 添加y轴名称
plt.xticks(range(0,70,4),values[range(0,70,4),1],rotation=45)
plt.title('2000-2017年季度生产总值散点图')## 添加图表标题
plt.savefig('../tmp/2000-2017年季度生产总值散点图.png')
plt.show()
# 代码 3-6
plt.figure(figsize=(8,7))## 设置画布
## 绘制散点1
plt.scatter(values[:,0],values[:,3], marker='o',c='red')
## 绘制散点2
plt.scatter(values[:,0],values[:,4], marker='D',c='blue')
## 绘制散点3
plt.scatter(values[:,0],values[:,5], marker='v',c='yellow')
plt.xlabel('年份')## 添加横轴标签
plt.ylabel('生产总值(亿元)')## 添加纵轴标签
plt.xticks(range(0,70,4),values[range(0,70,4),1],rotation=45)
plt.title('2000-2017年各产业季度生产总值散点图')## 添加图表标题
plt.legend(['第一产业','第二产业','第三产业'])## 添加图例
plt.savefig('../tmp/2000-2017年各产业季度生产总值散点图.png')
plt.show()
# 代码 3-7
plt.figure(figsize=(8,7))## 设置画布
## 绘制折线图
plt.plot(values[:,0],values[:,2],color = 'r',linestyle = '--')
plt.xlabel('年份')## 添加横轴标签
plt.ylabel('生产总值(亿元)')## 添加y轴名称
plt.xticks(range(0,70,4),values[range(0,70,4),1],rotation=45)
plt.title('2000-2017年季度生产总值折线图')## 添加图表标题
plt.savefig('../tmp/2000-2017年季度生产总值折线图.png')
plt.show()
# 代码 3-8
plt.figure(figsize=(8,7))## 设置画布
plt.plot(values[:,0],values[:,2],color = 'r',linestyle = '--',
marker = 'o')## 绘制折线图
plt.xlabel('年份')## 添加横轴标签
plt.ylabel('生产总值(亿元)')## 添加y轴名称
plt.xticks(range(0,70,4),values[range(0,70,4),1],rotation=45)
plt.title('2000-2017年季度生产总值点线图')## 添加图表标题
plt.savefig('../tmp/2000-2017年季度生产总值点线图.png')
plt.show()
# 代码 3-9
plt.figure(figsize=(8,7))## 设置画布
plt.plot(values[:,0],values[:,3],'bs-',
values[:,0],values[:,4],'ro-.',
values[:,0],values[:,5],'gH--')## 绘制折线图
plt.xlabel('年份')## 添加横轴标签
plt.ylabel('生产总值(亿元)')## 添加y轴名称
plt.xticks(range(0,70,4),values[range(0,70,4),1],rotation=45)
plt.title('2000-2017年各产业季度生产总值折线图')## 添加图表标题
plt.legend(['第一产业','第二产业','第三产业'])
plt.savefig('../tmp/2000-2017年季度各产业生产总值折线图.png')
plt.show()
###############################################################################
####################### 任务实现 #######################
###############################################################################
# 代码 3-10
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = 'SimHei' ## 设置中文显示
plt.rcParams['axes.unicode_minus'] = False
data = np.load('../data/国民经济核算季度数据.npz')
name = data['columns']## 提取其中的columns数组,视为数据的标签
values = data['values']## 提取其中的values数组,数据的存在位置
p = plt.figure(figsize=(12,12)) ##设置画布
## 子图1
ax1 = p.add_subplot(2,1,1)
plt.scatter(values[:,0],values[:,3], marker='o',c='r')## 绘制散点
plt.scatter(values[:,0],values[:,4], marker='D',c='b')## 绘制散点
plt.scatter(values[:,0],values[:,5], marker='v',c='y')## 绘制散点
plt.ylabel('生产总值(亿元)')## 添加纵轴标签
plt.title('2000-2017年各产业季度生产总值散点图')## 添加图表标题
plt.legend(['第一产业','第二产业','第三产业'])## 添加图例
## 子图2
ax2 = p.add_subplot(2,1,2)
plt.scatter(values[:,0],values[:,6], marker='o',c='r')## 绘制散点
plt.scatter(values[:,0],values[:,7], marker='D',c='b')## 绘制散点
plt.scatter(values[:,0],values[:,8], marker='v',c='y')## 绘制散点
plt.scatter(values[:,0],values[:,9], marker='8',c='g')## 绘制散点
plt.scatter(values[:,0],values[:,10], marker='p',c='c')## 绘制散点
plt.scatter(values[:,0],values[:,11], marker='+',c='m')## 绘制散点
plt.scatter(values[:,0],values[:,12], marker='s',c='k')## 绘制散点
## 绘制散点
plt.scatter(values[:,0],values[:,13], marker='*',c='purple')
## 绘制散点
plt.scatter(values[:,0],values[:,14], marker='d',c='brown')
plt.legend(['农业','工业','建筑','批发','交通',
'餐饮','金融','房地产','其他'])
plt.xlabel('年份')## 添加横轴标签
plt.ylabel('生产总值(亿元)')## 添加纵轴标签
plt.xticks(range(0,70,4),values[range(0,70,4),1],rotation=45)
plt.savefig('../tmp/2000-2017年季度各行业生产总值散点子图.png')
plt.show()
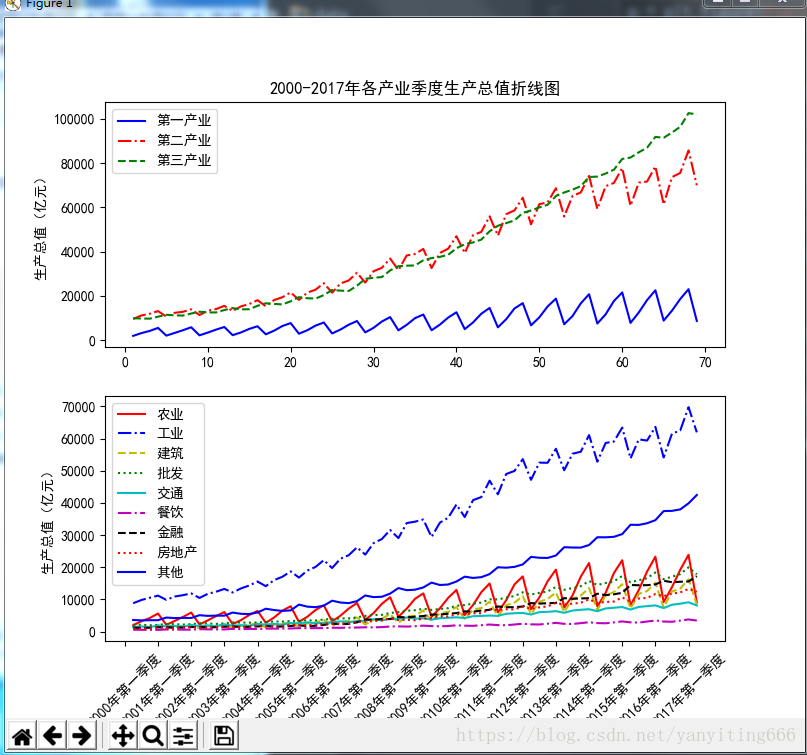
# 代码 3-11
p1 = plt.figure(figsize=(8,7))## 设置画布
## 子图1
ax3 = p1.add_subplot(2,1,1)
plt.plot(values[:,0],values[:,3],'b-',
values[:,0],values[:,4],'r-.',
values[:,0],values[:,5],'g--')## 绘制折线图
plt.ylabel('生产总值(亿元)')## 添加纵轴标签
plt.title('2000-2017年各产业季度生产总值折线图')## 添加图表标题
plt.legend(['第一产业','第二产业','第三产业'])## 添加图例
## 子图2
ax4 = p1.add_subplot(2,1,2)
plt.plot(values[:,0],values[:,6], 'r-',## 绘制折线图
values[:,0],values[:,7], 'b-.',## 绘制折线图
values[:,0],values[:,8],'y--',## 绘制折线图
values[:,0],values[:,9], 'g:',## 绘制折线图
values[:,0],values[:,10], 'c-',## 绘制折线图
values[:,0],values[:,11], 'm-.',## 绘制折线图
values[:,0],values[:,12], 'k--',## 绘制折线图
values[:,0],values[:,13], 'r:',## 绘制折线图
values[:,0],values[:,14], 'b-')## 绘制折线图
plt.legend(['农业','工业','建筑','批发','交通',
'餐饮','金融','房地产','其他'])
plt.xlabel('年份')## 添加横轴标签
plt.ylabel('生产总值(亿元)')## 添加纵轴标签
plt.xticks(range(0,70,4),values[range(0,70,4),1],rotation=45)
plt.savefig('../tmp/2000-2017年季度各行业生产总值折线子图.png')
plt.show()





















 880
880

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








