POVM 正算符 厄米矩阵

POVM

POVM是一组正算符（positive operator），它们的和等于单位算符。这些正算符描述了所有可能的测量结果，并且定义了每个测量结果出现的概率。通过测量算符的POVM可以得到连续谱物理量的测量结果，并且可以计算出每个测量结果出现的概率。

正算符

在量子力学中，正算符（positive operator）是指一个自伴（Hermitian）算符，即厄米算符，其所有本征值都是非负实数。正算符可以用于描述物理量的某些性质，例如概率、能量、密度等。

具体来说，对于一个Hilbert空间上的自伴算符A，如果其所有本征值都是非负实数，即A的本征值满足λi ≥ 0 (i = 1, 2, ..., n)，则称A为正算符。在实际应用中，我们通常将正算符表示为密度算符的形式，即一个非负的Hermite矩阵，其对角线元素表示态的概率分布。

正算符在量子力学中有广泛的应用。例如，在测量理论中，正算符可以用于描述测量结果的概率分布；在量子信息处理中，正算符可以用于描述量子态的纯度，即描述量子态与最大纯态之间的距离；在量子力学中，正算符还可以用于描述一些物理量的粒子数密度等。

总之，正算符是量子力学中一种重要的数学工具，可以用于描述量子态的某些性质，如概率、纯度、密度等，因此在量子信息处理、量子计算和量子测量等领域都有广泛的应用。

厄米矩阵

厄米矩阵和酉变换矩阵的区别，两者是不一样的。前者对应实空间的对称阵的概念，后者对应实空间正交阵的概念

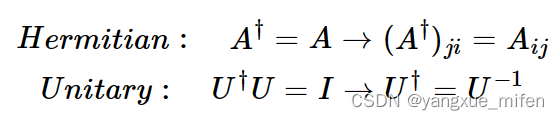
厄米矩阵的性质：

• 特征值为实数
• 特征向量相互正交
• 厄米矩阵的对角线元素一定为实数
• 酉变换不会改变厄米矩阵的特征值