1. 正则化和交叉验证

正则化和交叉验证是模型选择的两种方法。

模型的理解：

比如，对同一个多项式函数，不同系数即是不同的模型。

可以依据正则化和交叉验证来获得不用的模型系数，获得多个模型，并选择最优模型。

1. 正则化

结构风险 = 经验风险 + 正则化。

经验风险的理解： 模型在训练集中的平均损失，比如，去噪数据目标函数中的保真项，保证去噪图像和噪声图像接近。

1范数： 特征筛选，特征或参数可以为0，得到稀疏模型。
2范数： 防止过拟合，特征或者参数最多接近于0，但不会为0.

2. 交叉验证

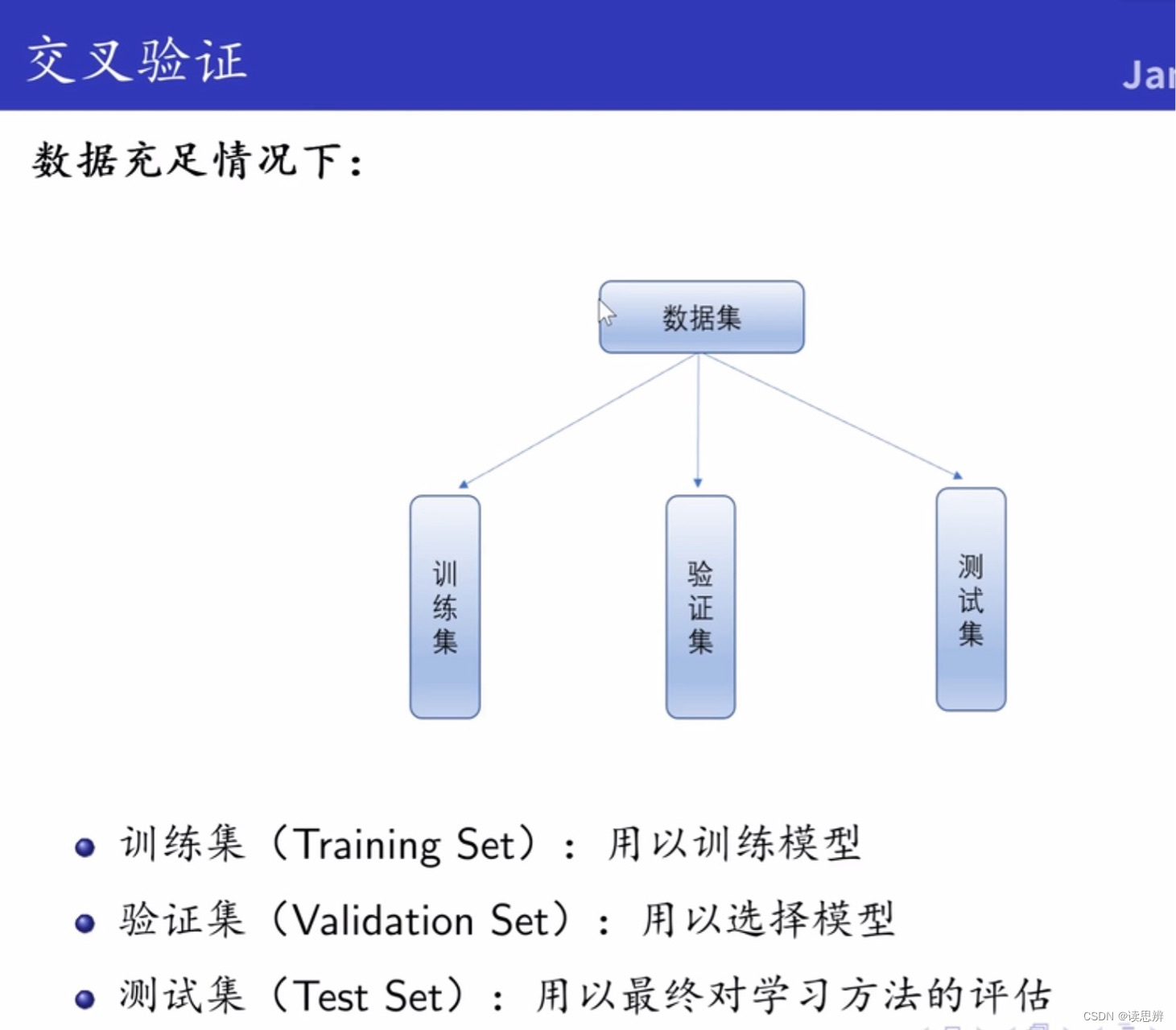
交叉验证的设计出发点是缓和数据不足现象，手段是重复利用数据。

2.1 简单交叉验证

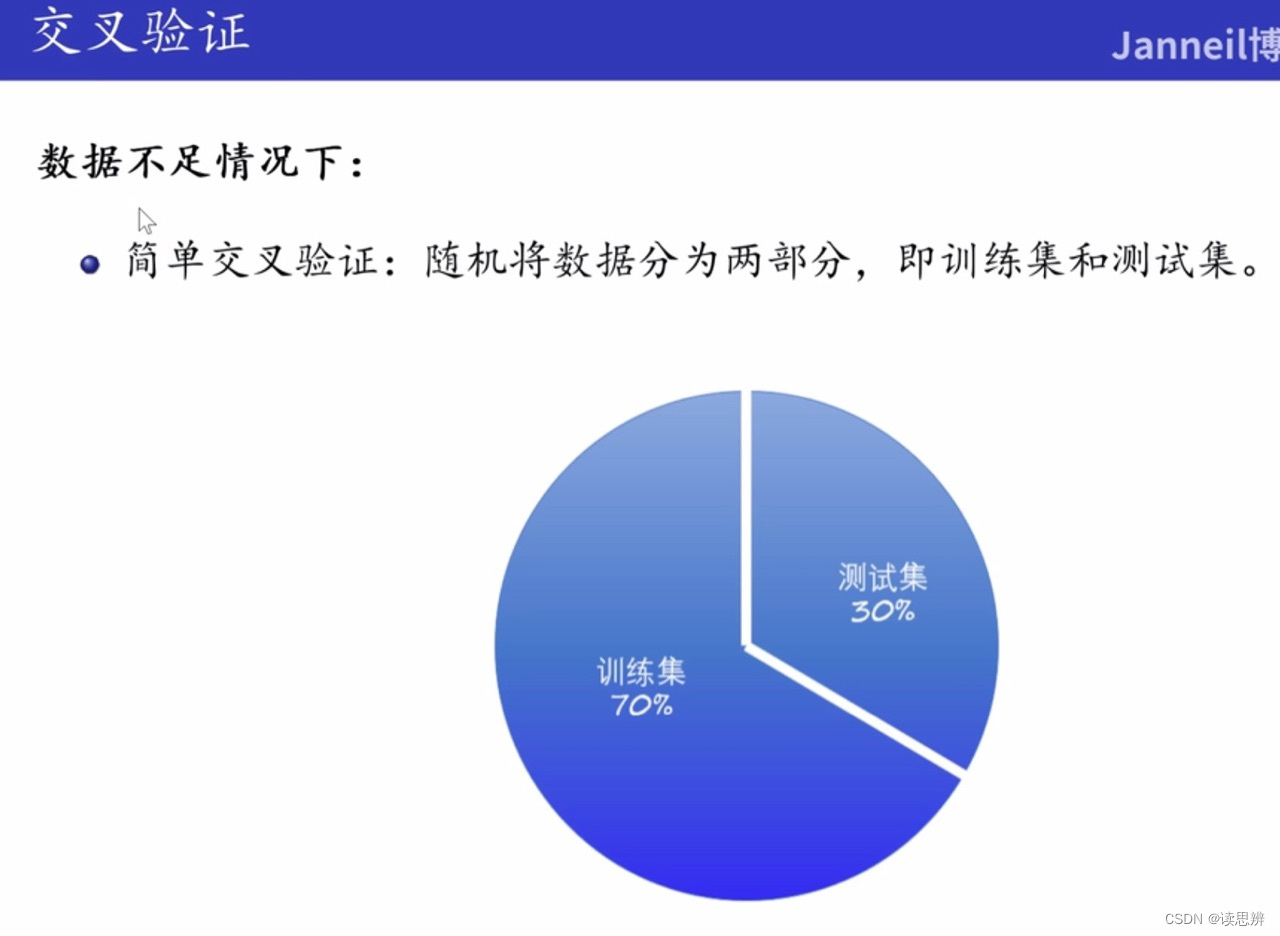
重复训练时，训练数据集中的样本会有重复

2.2. S折交叉验证 和留1交叉验证

N： 样本总个数
留1交叉验证用于数据非常缺乏的情况。

由交叉验证可得，训练集的不同划分方法可得到不同的模型（简单理解就是多项式函数不同的系数）。